3. Поток вектора Пойтинга в коаксиальном кабеле

Устройство коаксиального кабеля показано на рис. 281. К кабелю прило­жено постоянное напряжение U и протекает постоянный ток I.

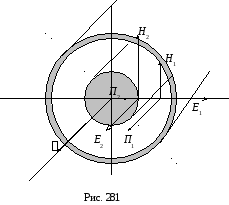
Особенностью режима работы коаксиального кабеля является то, что его электриче­ское и магнитное поле не выходит за пределы наружной оболочки.

Рассмотрим режим точки 1, расположенной в диэлектрике на расстоянии r от оси ка­беля. Линейная плотность заряда:.

Напряженность электрического поля: .

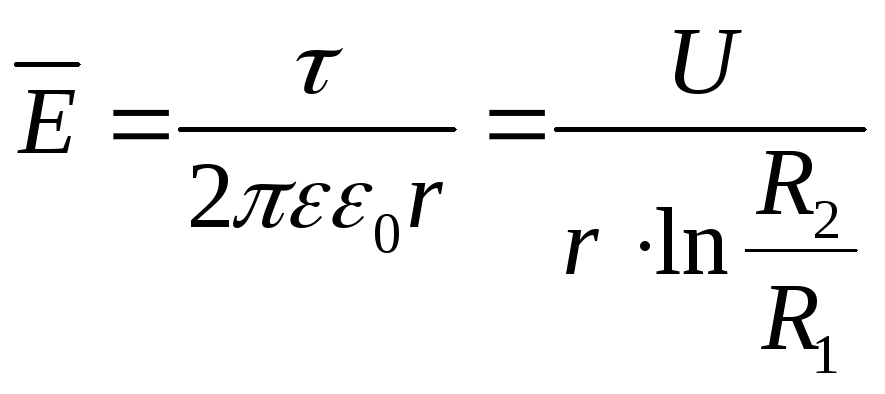Напряженность магнитного поля: .

Векторы поля инаправлены под углом в 90^о друг к другу.

Вектор Пойтинга:.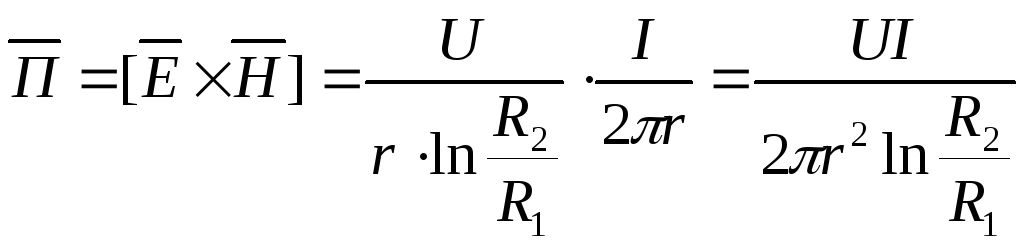

Вектор Пойтинга направлен вдоль оси кабеля по направлению тока I. По­ток вектора Пойтинга через поперечное сечение диэлектрика:

.

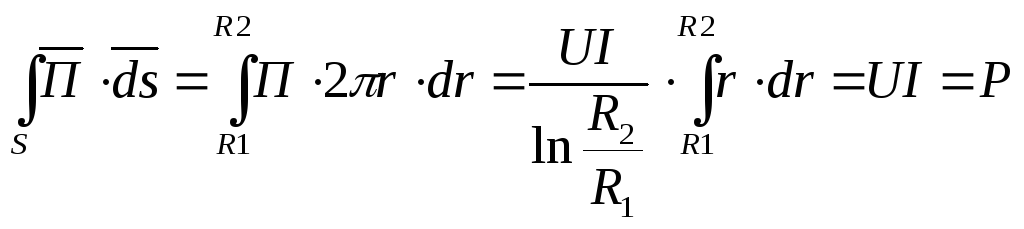Вывод: поток вектора Пойтинга через поперечное сечение диэлектрика равен переда­ваемой мощности Р, т. е. вся энергия от источника к приемнику передается электромагнит­ным полем, сосредоточенным в диэлектрике между жилой и оболочкой.

Рассмотрим режим точки 2, расположенной на наружной поверхности жилы.

Плотность тока в жиле кабеля: .

Напряженность электрического поля: .

Напряженность магнитного поля: .

Векторы поля инаправлены под углом в 90^о друг к другу.

Вектор Пойтинга: .

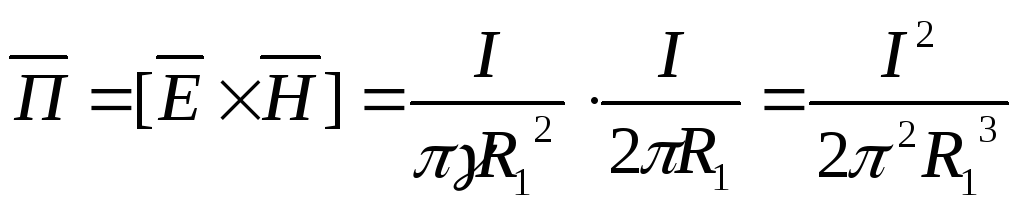Вектор Пойтинга направлен по радиусу к центру кабеля.

Поток вектора Пойтинга через боковую поверхность внутренней жилы:

.

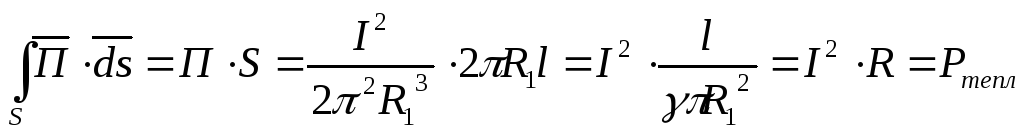Вывод: поток вектора Пойтинга через наружную поверхность жилы на­правлен внутрь провода и равен мощности тепловых потерь.

4. Уравнения Максвелла в комплексной форме

Если векторы поля иизменяются во времени по синусоидальному закону, то синусоидальные функции времени могут быть представлены ком­плексными числами и, со­ответственно, сами векторы будут комплексными:

В записанных выражениях черта снизу символа означает «комплекс», а черта сверху – «вектор», соответственно читается «комплекс-вектор».

Учитывая, что операции дифференцирования в комплексной форме соот­ветствует умножение комплексного изображения на множитель , то в урав­нениях Максвелла в комплексной форме время, как координата, в явной форме отсутствует.

С учетом принятых обозначений система основных уравнений Максвелла в ком­плексной форме получит вид:

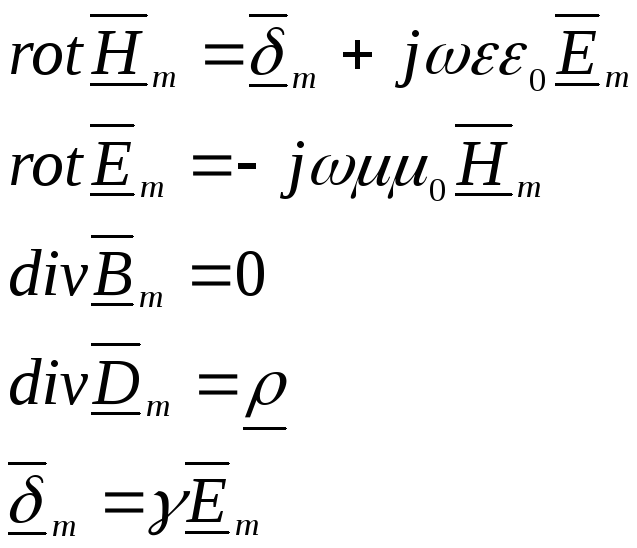
Комплексный вектор Пойтинга можно представить по аналогии с ком­плексной мощ­ностью:

.

Теорема Умова-Пойтинга в комплексной форме (без вывода):

.

5. Плоская гармоническая волна в диэлектрике

Плоской называется электромагнитная волна с плоским фронтом, у кото­рой векторы поля ивзаимно перпендикулярны и при соответствую­щем выборе направления осей координат будут зависеть только от одной про­стран­ственной координатыz и времени t. Волна называется гармонической, если век­торы поля иизменяются во времени по синусоидальному за­кону. Волна распространяется в однородном диэлектрике (), прово­димость которого равна нулю ().

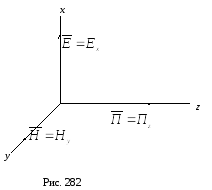
Выберем направления осей координат x, y, z так, чтобы вектор совпа­дал с осьюx , векторсовпадал с осьюy , тогда вектор Пой­тинга будет направлен вдоль осиz (рис. 282):

Система уравнений Максвелла в комплексной форме:

Раскроем операцию rot в декартовой системе координат и учтем, что век­торы поля содержат только по одной пространственной составляющей: ,:

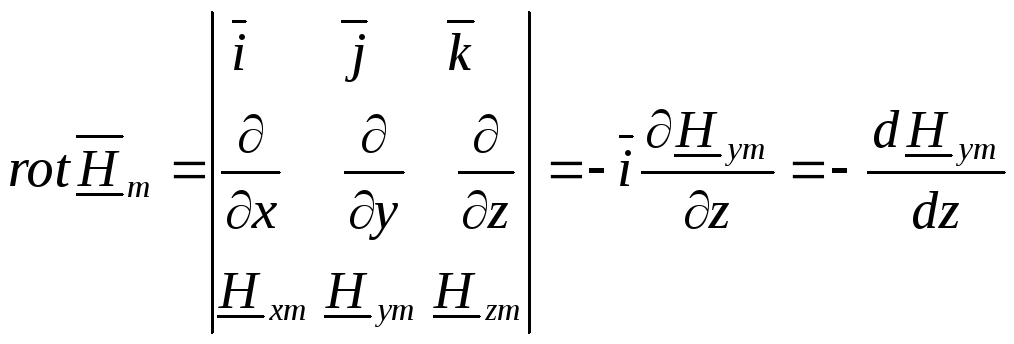(вектор направлен по оси х),

(вектор направлен по оси у)

Таким образом, система уравнений Максвелла получит вид:

Решим данную систему дифференциальных уравнений относительно од­ной из пере­менных, например, . Для этой цели продифференци­руем уравнение (2) по пе­ременнойz и выполним в него подстановку из уравне­ния (1):

,

где  фазовая скорость волны.

Таким образом получилось дифференциальное уравнение 2-го порядка с одной пе­ременной :

Решение для искомой функции:

где  корни характеристического уравнения:

В неограниченной однородной среде отраженные волны отсутствуют, по­этому при­мем С₂=0, С₁=Сe^j, тогда решение для искомой функции получит окончательный вид:

где .

Решение для переменной получим из уравнения (2) путем подста­новки в него найденного решения для переменной:

,

где - волновое сопротивление среды; для пустотыОм.

Перейдем от комплексного изображения функций к их оригиналам:

Т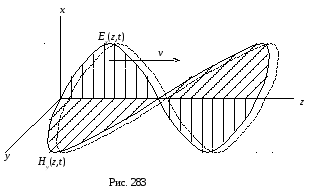аким образом, электромагнитное поле в диэлектрике распространяется в виде незату­хающих взаимно перпендикулярных в пространстве волнисо скоростью(рис. 283).

Отношение мгновенных значений волн в любой точке простран­ства и в любой момент времени постоянно и равно волновому сопротивлению.

Длиной волны λ называют расстояние, на котором фаза волны изменяется на 2π:

откуда следует, что

Каждая из волн переносит энергию в направлении своего движения, при этом объемные плотности энергий электрического и магнитного полей равны между собой.