8. Расчет мгновенных значений параметров режима графическим методом

При расчете мгновенных значений напряжений u(t) и токов i(t) в не­линейной цепи используются физические характеристики нелинейных эле­ментов, а именно: вольтамперная характеристика u=f(i) или i=f(u) для рези­стора, веберамперная характеристика i=f() или =f(i) для катушки и кулон­вольтная характеристика q=f(u) или u=f(q) для конденсатора.

В простейших случаях, если задан или может быть рассчитан закон из­менения во времени одной из спаренных физических величин, то закон измене­ния во времени другой ве­личины может быть получен графически методом проекции заданной функции на соответст­вующую физическую характеристику нелинейного элемента. В качестве примера рассмотрим графический расчет тока нелинейной катушки в режиме синусоидального напряжения (тока холо­стого хода трансформатора) (рис. 239).

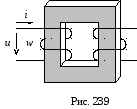
Пусть к зажимам катушки приложено напряжение u(t)=U_msint. Магнит­ный поток в сердечнике связан с напряжением уравнением индукции:

, откуда .

Графические диаграммы функций u(t) и ф(t) показаны на рис. 240. Справа приведена ве­бер-амперная характеристика ф(i) магнитной цепи в виде петли гис­терезиса, соответствующая расчетной амплитуде магнитного потока Ф_m. Расчет­ные точки искомой функции i(t) получа­ются методом проекции точек задан­ной функции ф(t) на вебер-амперную характери­стику ф(i) магнитной цепи.

Для построения графической диаграммы искомой функции i(t) исследуе­мый интервал времени (период Т) разбивается на отдельные отрезки . Для каждого момента времениt,t,t… определяются на диаграмме координаты точек заданной функцииф, ф, ф,…, ко­торые проектируется на на вебер-ам­перную характеристикуф(i) магнитной цепи. Найденные соответствующие зна­чения искомой функции i,i,i… в масштабе откладываются на диа­грамме для каждого момента времениt,t,t…. Отдельные точки соединяются плав­ной кривой, в результате чего получается графическая диаграмма искомой функцииi(t) (на рис. 240 показана жирной линией). Процедура построения графи­ческой диаграммы искомой функции i(t) на рис. 240 показана стрелками для 5 то­чек (0, 1, 2, 3, 4).

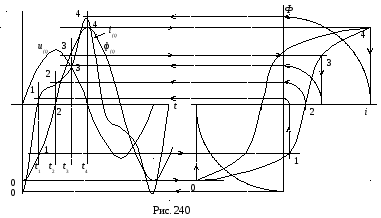
Анализ решения показывает, что намагничивающий ток катушки имеет несинусои­дальную форму и содержит в своем составе только нечетные гармо­ники.

9. Расчет мгновенных значений параметров режима гармоническими методами

В нелинейных цепях переменного тока происходят искажения форм кривых токов и напряжений. Несинусоидальные функции токов i(t) и напряже­ний u(t), как известно, можно представить в виде гармонических рядов Фурье. В гармонических методах расчета решение для искомых величин находят в виде суммы отдельных гармоник.

В простейших случаях решение для искомой функции в виде гармони­ческого ряда Фурье удается получить в результате разложения в ряд Фурье най­денного в общем виде ре­шения. В качестве примера рассмотрим расчет тока в нелинейной катушке (тока холостого хода трансформатора) (рис. 241). Чтобы по­лучить сравнительно простое решение, применим для катушки параллельную схему замещения (рис. 44). Вебер-амперную характеристику ка­тушки аппрокси­мируем уравнением степенного полинома:i_L() = a + b⁵.

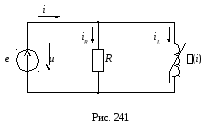
Пусть к зажимам катушки приложено напряжение u(t)=U_msin(t+90^o). Магнитное по­токосцепление катушки связано с напряжением уравнением ин­дукции:

, откуда .

Ток в резисторе определяется по закону Ома:

.

Ток в катушке найдется в результате подстановки функции (t) в уравне­ние аппрок­симации:

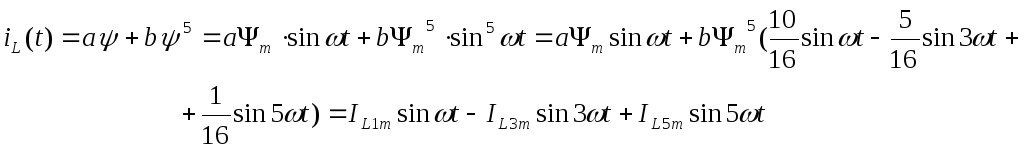
Ток источника определяется по первому закону Кирхгофа, при этом сло­жение гармо­ник токов одинаковой частоты можно выполнять в комплексной форме:

,

где I_1m= I_L1m+ jI_R1m= I_1me^j1.

Анализ решения показывает, что намагничивающий ток катушки имеет несинусои­дальную форму и содержит в своем составе только нечетные гармо­ники, при этом основная гармоника тока отстает от приложенного напряжения на угол  = _u  _i = 90^o  ₁.

Решение для искомой функции в виде суммы гармоник можно получить также мето­дом гармонического баланса. Суть этого метода состоит в том, что ожидаемое решение для функции f(t) представляется в виде суммы основной и нескольких высших гармоник:

,

где В₁, С₁, В₂, С₂… неизвестные коэффициенты, подлежащие определению. За­тем ампли­туды гармоник всех токов и напряжений выражаются через неизвест­ные коэффици­енты. По­сле этого балансируются коэффициенты для одинако­вых гармоник в уравнениях Кирхгофа, составленных для расчетной схемы. В результате получается система алгебраиче­ских урав­нений с неизвестными ко­эффициентами искомой функции, в результате решения которой оп­ределяются сами коэффициенты.

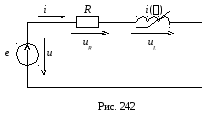
В качестве примера рассмотрим расчет режима в схеме рис. 242.

Пусть к выводам схемы приложено синусоидальное напряжение

, а вебер-амперная характеристика не­линей­ной катушки аппроксимирована уравнением .

Дифференциальное уравнение цепи будет иметь вид:

.

В качестве неизвестной функции, подлежащей определению, принимаем потокосцеп­ление (t), решение для которой будем искать в виде суммы 1-й и 3-й гармоник (четные гар­моники в решении отсутствуют):

,

где В₁, С₁, В₃, С₃  неизвестные коэффициенты.

Выражаем ток и напряжения на отдельных участках схемы через искомую функцию (t):

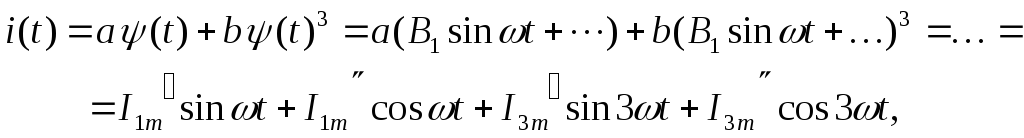
где амплитуды гармоник состоят в некоторой функциональной зависимости от неизвестных коэффициентов В₁, С₁, В₃, С₃.

.

.

Теперь составляется баланс коэффициентов для отдельных гамоник (уравнения гар­монического баланса) в соответствии со 2-м законом Кирхгофа u(t) = u_R(t) + u_L(t):

,

,

,

.

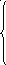
В алгебраических уравнениях гармонического баланса отдельные слагае­мые в левой части являются некоторыми функциями неизвестных коэффициен­тов В₁, С₁, В₃, С₃. Решение этой системы уравнений представляет зачастую большую математическую трудность.

В виду больших математических осложнений, возникающих при опреде­лении неиз­вестных коэффициентов, метод гармонического баланса оказывается мало эффективным и применяется редко.