3. Расчет неразветвленной магнитной цепи

Пусть требуется выполнить расчет магнитной цепи электромагнитного реле, эскизный вид которого и схема магнитной цепи показана на рис. 2а, б. Бу­дем считать, что геометриче­ские размеры участков и основная кривая намагни­чивания материала B=f(H) заданы. Воз­можны два варианта постановки задачи:

а) по заданному магнитному потоку Ф (или индукции В в заданном сече­нии) требуется определить ток I в обмотке – прямая задача;

б) по заданному току в обмотке I требуется определить магнитный поток Ф или ин­дукцию В в заданном сечении – обратная задача.

Прямая задача сравнительно просто решается аналитическим путем. Пусть магнитный поток Ф известен. Тогда 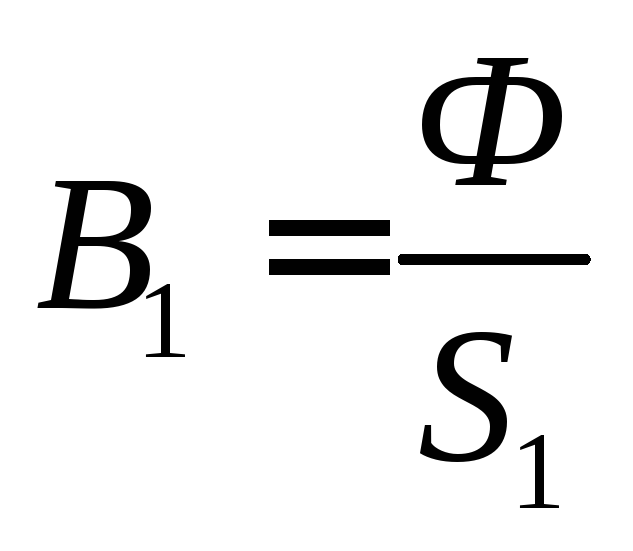;;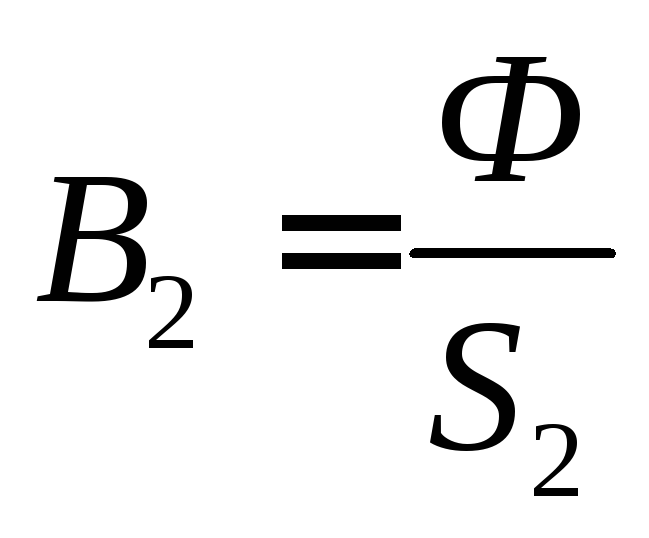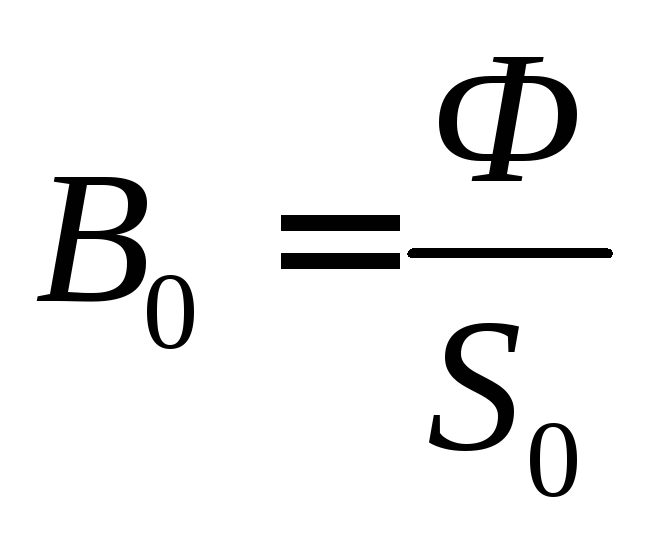. Значения координатН₁ и Н₂ находим по заданной кривой намагничивания В=f(Н) для расчетных точек В₁ и В₂. Значение напряженно­сти поля в зазоре определяем из уравнения .

По 2-ому закону Кирхгофа для схемы замещения находим значение МДС:

. Искомый ток в обмотке равен: .

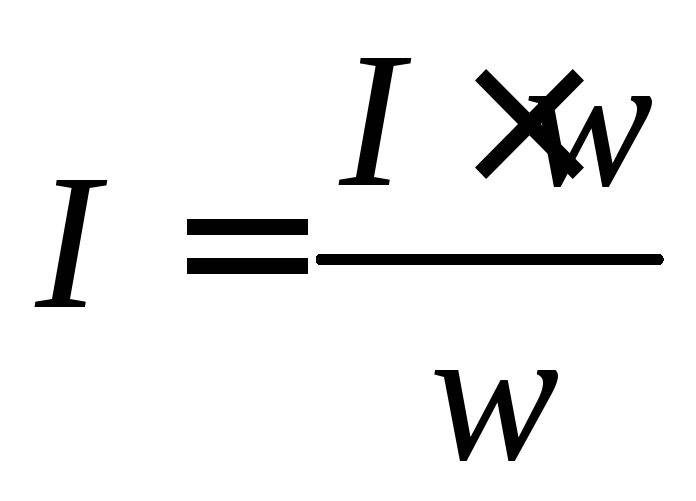Обратная задача решается методом последовательных приближений. Пусть задан ток в обмотке реле I и требуется определить магнитный поток Ф.

Задаются в первом приближении значением магнитного потока и, ре­шая прямую задачу, определяют значение токав первом приближении. С учетом неравенствазадаются значением магнитного потокаво вто­ром приближении и определяют значение токаво втором приближении. Циклы расчета или итерации выполняются до достижения требуемой точности определения искомой величины. Учитывая, что решение прямой задачи явля­ется сравнительно простым и нетрудоемким, то и решение обратной задачи, требующее выполнения нескольких циклов расчета, является относительно не­трудоемким и может вы­полняться вручную, без помощи ЭВМ.

Как прямая, так и обратная задача могут быть решены графически мето­дом сложения ВАХ отдельных участков. Для этой цели на основе заданных кривой намагничивания В=f(Н) и геометрических размеров отдельных участков магнитной цепи (l, s) производится расчет веберамперных характеристик (ВАХ) для отдельных участков .

Как правило, расчетные точки ВАХ для всех участков сводят в общую таблицу:

Ф	Вб	Задают	…	…	…	…	…	…	…
В1	Тл	Ф/S1
В2	Тл	Ф/S2
В0	Тл	Ф/S0
Н1	А/м	H1=f(B1)
Н2	А/м	H2=f(B2)
Н0	А/м	H1=8105B0
U1	А	H1l1
U2	А	H2l2
U0	А	H0δ0
Iw	А

П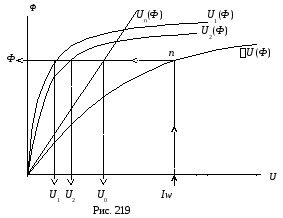о результатам расчета в одной системе координат строятся графические диаграммы ВАХ всех участков (рис. 219):

Производится графическое сложение ВАХ отдельных участков согласно схеме цепи. В рассматриваемом примере производится последовательное (по оси U) сложение ВАХ U₁(Ф), U₂(Ф), и U₀(Ф), в результате сложения получается входная ВАХ . На входной ВАХ определяется положение рабочей точкиn для и выполняется графи­ческое решение для всех величин (на рис. 219 показано стрелками).