3. Синтез двухполюсника лестничной (цепной) схемой

Непрерывной дробью называется математическое уравнение вида:

.

Пусть электрическая цепь имеет лестничную (цепную) схему (рис. 197).

Методом свертки выразим входное сопротивление и входную проводи­мость цепной схемы:

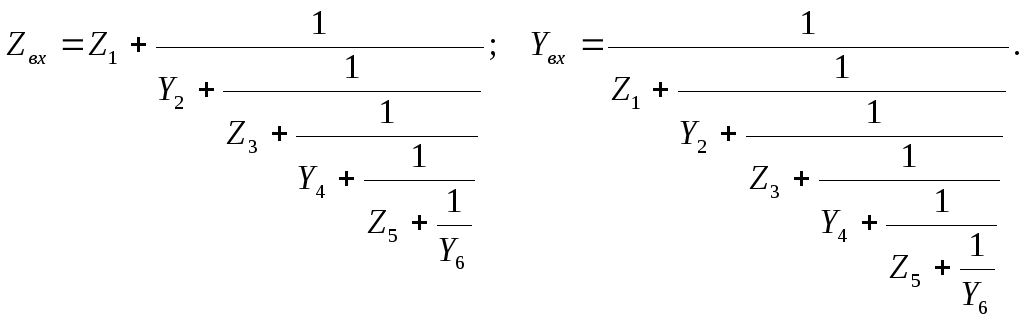
Входное сопротивление и входная проводимость цепной схемы выража­ется уравне­нием, которое имеет структурную форму непрерывной дроби.

Таким образом, задача синтеза двухполюсника, заданного входной функ­цией или, сводится к преобразованию этой функции к виду непре­рывной дроби и последующему переходу к соответствующей этой дроби цепной схеме.

В математике разработаны способы преобразования простых дробей к виду непре­рывной дроби. Порядок такого преобразования показан на конкрет­ном примере:

По аналогичной форме выполняется преобразование к виду непрерывной дроби вы­ражений входных функций или. Процесс преобразования можно представить следующим образом:

1. располагают полиномы N(p) и М(p) либо по убывающим, либо по воз­растающим степеням р;

2. делят N(p) на М(p) как многочлен на многочлен, в результате получают частное Ч₁(p) и некоторый остаток О₁(p);

3. делят М(p) на остаток О₁(p) как многочлен на многочлен, в результате получают частное Ч₂(p) и некоторый остаток О₂(p);

4. и т. д. продолжают процесс деления до получения частного без ос­татка;

5. в соответствии с полученной непрерывной дробью составляют цепную схему за­мещения в операторной форме;

6. переходят к физическим параметрам элементов схемы (к электриче­ской схеме) на основе формул соответствия: .

На основании изложенного процесс последовательного деления можно представить следующей схемой:

выходные

величины

При делении многочлена на многочлен следят за тем, чтобы в процессе деления в ча­стном содержались только положительные члены, и чтобы они не содержали множитель р в степени больше 1.

4. Синтез двухполюсника методом разложения входной функции на простейшие составляющие

Выражение для входной функции илимате­матически можно разложить на простые слагаемые по форме:

.

Первые два слагаемые выделяют из входной функции путем деле­нияN(p) на М(p) как многочлен на многочлен с целью понижения показателя числителя до значения n=m1, в результате получают частное и неко­торый остаток N₁(p). Остаток функ­ции раскладывают на простые слагаемые по известной в математике формуле разложения:

,

где р₁, р₂, …p_m – корни уравнения М(p)=0,  коэффициенты, опре­деляемые со­гласно формуле разложения.

После разложения входной функции на простые слагаемые каждому сла­гаемому подбирают соответствующий ему участок операторной схемы, отдель­ные участки соеди­няют между собой последовательно для функцииили параллельно для функции, и таким образом получают схему цепи, соот­ветствующей входной функцииили.

Рассмотрим простейшие схемы соединения элементов и соответствующие им опера­торные изображения.

;

 ;

 ;













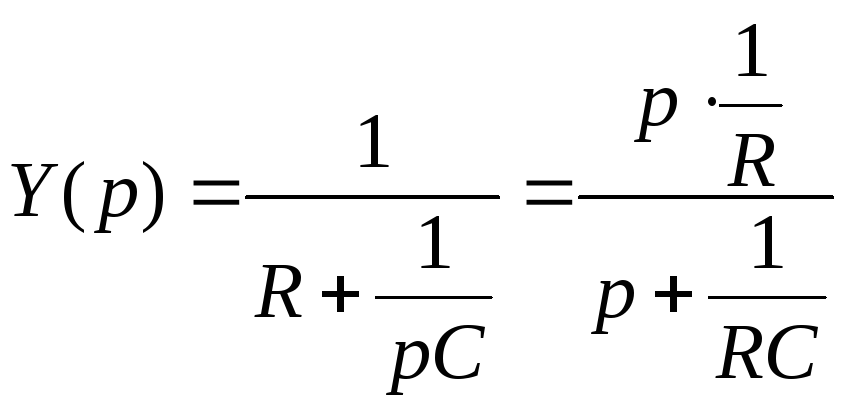
Рассмотрим, каким образом может быть реализовано каждое слагаемое входной функции Z(p). Первому слагаемому соответствует катушка индук­тивности, так как. Второму слагаемомусоответствует резистор.

Если среди корней р_к имеется корень , то его подстановка в формулу разложе­ния дает выражение вида, которое в схеме может быть реализовано конденсатором, так как.

Если среди корней р_к имеются мнимые сопряженные корни и, то их подстановка в формулу разложения дает следующее выражение ():

,

которому соответствует параллельный резонансный контур, состоящий из эле­ментов L и С, для которого и.

Если среди корней р_к имеется вещественный отрицательный корень , то его подстановка в формулу разложения дает выражение вида, которое может быть реали­зовано схемой с параллельным соединением элемен­товR и С при соотношении , и.

Слагаемые, соответствующие комплексно сопряженным корням , могут быть реализованы более сложными методами, рассмотре­ние которых здесь не приводится.