- •Теоретические основы электротехники
- •Часть 1. Теория линейных цепей (продолжение) т10. Четырехполюсники и фильтры
- •Уравнения четырехполюсника
- •2. Схемы замещения четырехполюсника
- •3. Определение коэффициентов четырехполюсника
- •4. Способы соединения четырехполюсников
- •5. Характеристические параметры симметричного четырехполюсника
- •6. Основные понятия и определения электрических фильтров
- •Коэффициентом передачи напряжения фильтра называется отношение комплексных выходного напряжения ко входному:
- •8. Фильтры нижних частот типа к
- •9. Фильтры верхних частот типа к.
- •10. Полосовые фильтры
- •11. Заграждающие фильтры
- •Т11. Электрические цепи с распределенными параметрами
- •Общие определения
- •2. Дифференциальные уравнения цепи с распределенными параметрами
- •3. Решение уравнений линии с распределенными параметрами в установившемся синусоидальном режиме
- •4. Волновые процессы в линии с распределенными параметрами.
- •5. Линия с распределенными параметрами в различных режимах
- •6. Линия с распределенными параметрами без искажений
- •7. Линия с распределенными параметрами без потерь
- •Графические диаграммы названных функций показаны на рис. 2.
- •8. Переходные процессы в линии с распределенными параметрами
- •9. Расчет падающих волн в линии с распределенными параметрами при подключении ее к источнику эдс
- •10. Расчет отраженных волн в линии с распределенными параметрами при подключении ее к источнику эдс
- •Расчет переходного процесса в линии с учетом многократных отражений волн
- •Т12. Синтез электрических цепей
- •2. Свойства входных операторных функций пассивных электрических цепей
- •3. Синтез двухполюсника лестничной (цепной) схемой
- •4. Синтез двухполюсника методом разложения входной функции на простейшие составляющие
- •Часть 2. Теория нелинейных цепей т1. Нелинейные цепи постоянного тока
- •1. Нелинейные элементы, их характеристики и параметры
- •2. Нелинейные цепи и их свойства
- •3. Графический метод расчета простых нелинейных цепей
- •4. Графический метод расчета нелинейной цепи с несколькими источниками эдс
- •5. Комбинированный графоаналитический метод расчета нелинейной цепи с одним или двумя нелинейными элементами
- •6. Аппроксимация вах нелинейных элементов
- •7. Аналитические методы расчета нелинейных цепей
- •Т2. Нелинейные магнитные цепи постоянного потока
- •1. Основные понятия и законы магнитной цепи
- •3. Расчет неразветвленной магнитной цепи
- •4. Расчет разветвленной магнитной цепи
- •5. Расчет магнитной цепи с постоянным магнитом
- •Т3. Нелинейные цепи переменного тока.
- •1. Общая характеристика нелинейных цепей переменного тока и методов их исследования
- •2. Замена несинусоидальных функций u(t) и I(t) эквивалентными синусоидальными
- •3. Методы расчета нелинейных цепей переменного тока на основе вах для эквивалентных синусоид
- •4. Резонансные явления в нелинейных цепях
- •5. Нелинейная катушка с сердечником на переменном токе
- •6. Трансформатор с сердечником и его схема замещения
- •7. Управляемая катушка индуктивности
- •8. Расчет мгновенных значений параметров режима графическим методом
- •9. Расчет мгновенных значений параметров режима гармоническими методами
- •10. Преобразователь частоты в 3 раза на нелинейных катушках
- •11. Расчет мгновенных значений параметров режима методом численного интегрирования системы дифференциальных уравнений.
- •Т4. Переходные процессы в нелинейных цепях
- •1. Общая характеристика переходных процессов в нелинейных цепях
- •Расчет переходного процесса методом интегрируемой аппроксимации
- •3. Расчет переходного процесса методом кусочно-линейной аппроксимации
- •4. Расчет переходного процесса методом линеаризации дифференциального уравнения
- •5. Расчет переходного процесса методом численного интегрирования дифференциального уравнения
- •Т5. Магнитные цепи переменного потока.
- •1. Потери в сердечниках из ферромагнитного материала при периодическом перемагничивании.
- •2. Расчет магнитной цепи переменного потока комплексным методом
- •Часть 3. Теория электромагнитного поля т1. Электростатическое поле
- •1. Основные понятия и определения
- •2.Уравнения электростатического поля в интегральной и дифференциальной форме
- •3. Граничные условия в электростатическом поле
- •4. Уравнение Пуассона и Лапласа. Теорема единственности решения
- •5. Электростатическое поле осевых зарядов
- •6. Электростатическое поле и емкость двухпроводной линии
- •7. Электростатическое поле и емкость цилиндрического провода, расположенного над проводящей плоскостью (землей)
- •8. Поле многопроводной линии. Метод зеркальных отображений
- •9. Электрическое поле трехфазной линии электропередачи
- •Т2. Электрическое поле постоянного тока
- •1. Законы электрического поля в интегральной и дифференциальной формах
- •2. Методы расчета электрических полей постоянного тока
- •T3. Магнитное поле постоянных токов
- •1. Уравнения магнитного поля в интегральной и дифференциальной формах
- •2. Векторный потенциал магнитного поля
- •3. Скалярный потенциал магнитного поля
- •4. Магнитное поле цилиндрического проводника с током
- •5. Магнитное поле двухпроводной линии
- •6. Взаимная индуктивность двух параллельных линий
- •7. Магнитное поле сложной системы проводов с током
- •8. Механические силы в магнитном поле
- •Т4. Переменное электромагнитное поле
- •Основные уравнения Максвелла и их физический смысл
- •Для стационарного поля и, тогда первое уравнение Максвелла превращается в уравнения магнитного поля постоянного тока:
- •2. Теорема Умова-Пойтинга для электромагнитного поля
- •3. Поток вектора Пойтинга в коаксиальном кабеле
- •4. Уравнения Максвелла в комплексной форме
- •5. Плоская гармоническая волна в диэлектрике
- •6. Плоская гармоническая волна в проводящей среде
- •7. Поверхностный эффект в плоском листе
- •8. Поверхностный эффект в круглом проводе
7. Линия с распределенными параметрами без потерь
Для
кабельных линий с распределенными
параметрами, работающих на высоких
частотах (линии связи), реактивные
параметры значительно превосходят
активные
![]() и
и![]() .
При расчете режимов таких линий можно
без особого ущерба для точности расчета
пренебречь активными параметрами и
принять их равными нулю
.
При расчете режимов таких линий можно
без особого ущерба для точности расчета
пренебречь активными параметрами и
принять их равными нулю![]() .
В таком случае линия становится идеальной
или без потерь.
.
В таком случае линия становится идеальной
или без потерь.
Волновое сопротивление линии без потерь:
![]()
является чисто активным и не зависит от частоты.
Постоянная распространения линии без потерь:
![]() ,
,
где
![]()
В
линии без потерь отсутствует затухание
сигнала
![]() ,
а фазовая скоростьv
не зависит от частоты, следовательно,
линия без потерь является неискажающей.
,
а фазовая скоростьv
не зависит от частоты, следовательно,
линия без потерь является неискажающей.
Учитывая
математические соотношения, что
![]() ,
и
,
и
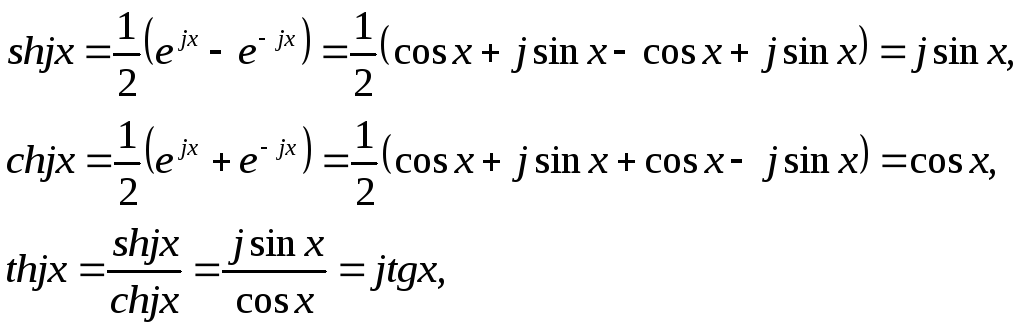
преобразуем комплексные уравнения установившегося синусоидального режима линии:
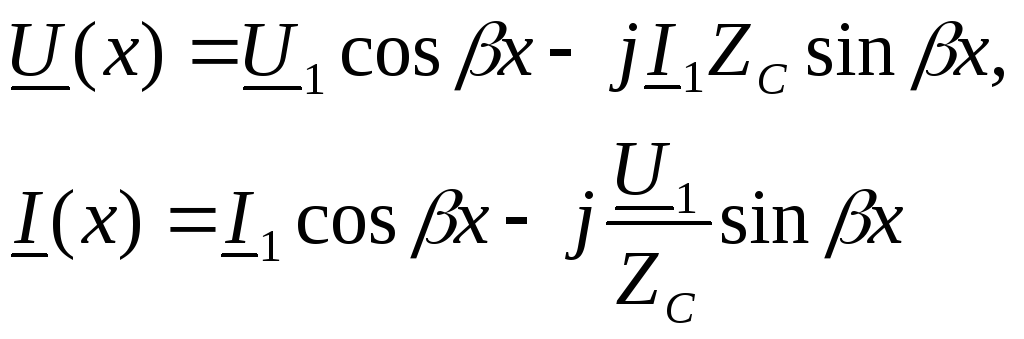
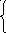 при
отсчете координаты х от начала линии,
при
отсчете координаты х от начала линии,
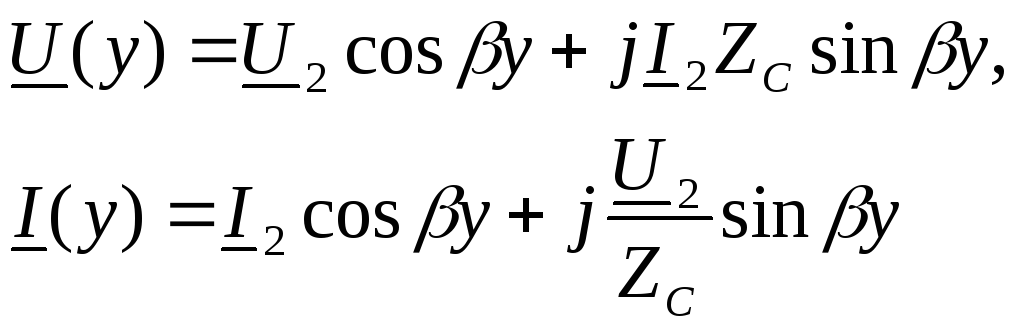
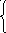 при
отсчете координаты y от конца линии,
при
отсчете координаты y от конца линии,
![]() входное
сопротивление линии.
входное
сопротивление линии.
Режим
линии без потерь определяется свойствами
(параметрами) самой линии и величиной
и характером нагрузки
![]() на ее конце. Исследуем работу линии в
различных режимах нагрузки.
на ее конце. Исследуем работу линии в
различных режимах нагрузки.
1.Режим
согласованной нагрузки:
![]() .
.
Учитывая,
что
![]() ,
комплексные уравнения линии получат
следующий вид:
,
комплексные уравнения линии получат
следующий вид:
![]()
 при
отсчете координаты y от конца линии,
при
отсчете координаты y от конца линии,
![]() входное
сопротивление линии.
входное
сопротивление линии.
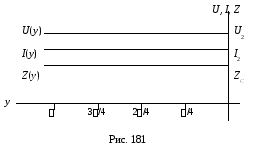
В режим согласованной нагрузки напряжение u(t,y) и ток i(t,y) состоят только из падающих волн, которые распространяются от начала линии к ее концу без затухания. Действующие значения напряжения U(y) и тока I(y) не зависят от координаты у и во всех точках линии имеют одинаковые значения.
Входное
сопротивление линии
![]() равно волновому
равно волновому![]() и не зависит от длины линии. Графические
диаграммы названных функций показаны
на рис. 181
и не зависит от длины линии. Графические
диаграммы названных функций показаны
на рис. 181
2.Режим
холостого хода:
![]()
![]() Комплексные уравнения режима линии
получат вид:
Комплексные уравнения режима линии
получат вид:
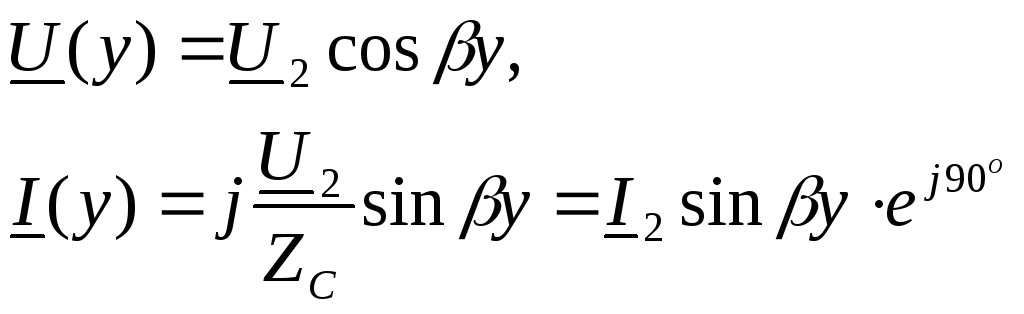
 при
отсчете координаты y от конца линии,
при
отсчете координаты y от конца линии,
![]() входное
сопротивление линии.
входное
сопротивление линии.
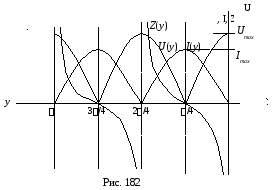
Входное сопротивление линии Z1(у), является чисто реактивным, его величина и характер зависят от длины линии.
Графические диаграммы названных функций показаны на рис. 2.
Режим
линии, при котором в некоторых ее точках
наблюдаются максимальные значения
напряжения (тока) или пучности, а в других
ее точках – нулевые значения этих
величин или узлы, получил название
в технике режима стоячих волн. Узлы и
пучности для одной и той же величины
следуют друг за другом через отрезки
равные
![]() где
где![]()
длина волны, при этом узлы одной величины
совпадают с пучностями другой.
длина волны, при этом узлы одной величины
совпадают с пучностями другой.
Режим стоячих волн физически можно объяснить как результат наложения падающей и наложенной волн с одинаковыми амплитудами. В точках линии, в которых мгновенные значения падающей и отраженной волн всегда совпадают, образуются пучности, а в точках, где эти значения складываются с противоположным знаком (в противофазе), образуются узлы.
Следует
отметить, что режим стоячих волн имеет
место в линии без потерь при чисто
реактивной нагрузке
![]() любой величины (
любой величины (![]() ).
При реактивной нагрузке энергия,
доставляемая падающей волной в конец
линии, полностью отражается, при этом
амплитуда отраженной волны равна
амплитуде подающей волны. Входное
сопротивление линии при реактивной
нагрузке
).
При реактивной нагрузке энергия,
доставляемая падающей волной в конец
линии, полностью отражается, при этом
амплитуда отраженной волны равна
амплитуде подающей волны. Входное
сопротивление линии при реактивной
нагрузке![]() является чисто реактивным:
является чисто реактивным:
![]() где
где
![]() .
.
3.Режим
произвольной нагрузки:
![]() .
.
Расчет
режима линии производится путем
совместного решения ее комплексных
уравнений и уравнений закона Ома:![]() и
и![]() .
При произвольной несогласованной
нагрузке в конце линии происходит
частичное отражение волн, при этом
амплитуды отраженных волн напряжения
и тока будут меньше амплитуд падающих
волн. Распределение действующих
значений напряжения и тока вдоль
линии будет носить волнообразный
характер рис. 3, при этом максимумы и
минимумы функции будут следовать друг
за другом через интервал
.
При произвольной несогласованной
нагрузке в конце линии происходит
частичное отражение волн, при этом
амплитуды отраженных волн напряжения
и тока будут меньше амплитуд падающих
волн. Распределение действующих
значений напряжения и тока вдоль
линии будет носить волнообразный
характер рис. 3, при этом максимумы и
минимумы функции будут следовать друг
за другом через интервал![]() .
.
Степень
несогласованности сопротивления
нагрузки
![]() с волновым сопротивлением линииZC
характеризуется коэффициентом стоячей
волны:
с волновым сопротивлением линииZC
характеризуется коэффициентом стоячей
волны:
![]()
В реальных условиях для согласования нагрузки с линией применяются специальные согласующие устройства.