Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Пензенский Государственный Университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

умк_Цывис_Функции_Интеграл. исчисл

..pdf

Скачиваний:

Добавлен:

18.05.2015

Размер:

4.7 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 89 / 369 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

5. Решая систему (8), найдем критические точки и вспомогатель- ный множитель λ . Система уравнений представляет собой необходимые условия существования условного экстремума: не всякая критическая точ- ка M0 (x0 , y0 ) , координаты x0 и y0 которой удовлетворяют системе урав-

нений (8), будет точкой условного экстремума.

6. Для исследования характера критической точки требуется про- вести дополнительный анализ приращения z в окрестности критической точки M0 , лежащей на линии L.

Заметим, что левые части уравнений системы (8) являются частными

производными вспомогательной функции трех переменных	F (x, y,λ) , на-
зываемой функцией Лагранжа:
F (x, y,λ) = f (x, y) + λϕ(x, y) ,	(9)

где f (x, y) – заданная функция, ϕ(x, y) – левая часть уравнения связи.

Таким образом, можно ввести правило нахождения точек условного экстремума для функции двух переменных:

1)строим функцию Лагранжа по формуле (9);

2)находим частные производные по x, y и λ , составляем систему (8). Решения данной системы – точки возможного условного экстремума (кри- тические точки функции Лагранжа);

3)определяем знак z (приращения функции) в окрестностях кри- тических точек по тем точкам окрестности, которые удовлетворяют урав- нению связи ϕ(x, y) = 0 , т.е. лежат на линии L.

Если при этом будем иметь, что для любых указанных точек М, лежа- щих на L z = f (M ) − f (M 0 ) > 0 , то M0 (x0 , y0 ) – точка условного мини- мума, если же z = f (M ) − f (M 0 ) < 0 , то M0 (x0 , y0 ) – точка условного максимума.

Пример 2. Найти экстремум функции z = x2 + y2 + 2 при условии x + y = 2 (уравнение связи).

Решение. В примере 1 аналогичную задачу решили методом исклю- чения или методом сведения к исследованию на экстремум функции одной переменой. В этом примере найдем условный экстремум, используя функ- цию Лагранжа, для этого поступим следующим образом:

1) строим функцию Лагранжа

f (x, y,λ) = x2 + y2 + 2 + λ(x + y − 2) ;

2) составим систему уравнений для определения критических точек

F (x, y,λ)

∂F = 2x + λ = 0					x = − λ
∂x									2
∂x									2
∂F		= 2 y + λ = 0			y = −				λ
∂y		= 2 y + λ = 0			y = −				2
∂y					λ		λ		2
∂F	= x + y − 2		= 0		λ	−	λ	= −2.
∂λ	= x + y − 2		= 0	−	2	−	2	= −2.
∂λ					2		2

Откуда имеем λ = −2 , а критическая точка M0 (1,1) .
3)	проведем дополнительный анализ приращения функции							z в
критической точке		M0 (1,1) . Имеем: пусть				x0 удовлетворяет уравнению
связи x0 + y = 2 , тогда y0 = 2 − x0 , а, следовательно,							M (x0 ,2 − x0 )
	z = f (M ) − f (M 0 ) = f (x0 ,2 − x0 ) − f (1,1) =
	= x2 + (2 − x )2 + 2 − 4 = 2x			2	− 4x + 2 = 2(x2 − 1)2 > 0.
	0	0	0		0		0
для всех	M ¹ M 0	и для точек	М,	координаты которых удовлетворяют
уравнению связи		(x + y = 2) , т.е.		f (M ) > F (M 0 ) ,			следовательно,	точка
M0 (1,1) –	точка условного минимума, z(1,1) = 4 .
Полученный результат полностью совпадает с результатом примера 1.
Пример 3. Найти условный экстремум функции z = 8 − 2x − 4 y								при
условии	x2 + 2 y2 = 12 .
Решение.
1) составим функцию Лагранжа
	F (x, y,λ) = 8 − 2x − 4 y + λ(x2 + 2 y2 −12) ;.
2) найдем критические точки функции						F (x, y,λ)

∂F (x, y,λ)				= 2xλ − 2 = 0
∂F (x, y,λ)

∂F	∂x
∂F	= 4 yλ − 4 = 0
∂y	= 4 yλ − 4 = 0
∂y
∂F	= x	2	+ 2 y2 −12		= 0
∂λ	= x	2	+ 2 y2 −12		= 0
∂λ

Откуда

λ1 = −0,5x1 = −2

y1 = −2

		x =		1
				λ

				1
		y =

				λ

1		+	2		= 12

	λ2		λ2

λ2 = 0,5
		= 2
x2
	y2	= 2


Таким образом, критические точки							M1(−2; −2) и M 2 (2;2) ;
3) уравнение связи x2 + 2 y2 = 12 –							это эллипс с полуосями a = 2
								3
и b =
	6 . Для исследования на условный экстремум в критических точках
M1 и	M 2 функции z = 8 - 2x - 4 y			запишем уравнение эллипса в пара-
метрической форме x = 2			cost, y =			sin t, t Î[0;2p] .
		3			6

Тогда функция z = 8 - 2x - 4 y примет вид z = 8 - 4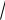3 cos t - 46 sin t .

Это функция одной переменой t. Определим локальный экстремум данной функции, тем самым решим задачу об условном экстремуме исходной за- даче. Находим производные первого и второго порядка

′

′′

6 cos t;

= 4

3 cos t + 4

6 sin t .

z (t) = 4 3 sin t − 4

z (t)

Найдем значение

′′

в точках M1

M 2 . Значение параметра t1 ,

z (t)

которое

соответствует

точке

будет

удовлетворять

условиям

−2

-2

z¢¢(t ) = -4

= -

; sin t =

+ 4 6

= -12 < 0 .

cos t

Тогда

Тогда, в точке

функция

z(t) имеет локальный экстремум, а это

значит, что в точке

M1 исходная функция имеет условный локальный

максимум

z(−2;2) = 20 .

Таким же образом, для точки M 2 (2;2) имеем:

cos t2 =

;

sin t2 =

;

z¢¢(t2 ) = 4 ×

+ 4

= 4

+ 8

> 0 .

В точке t2 функция

z(t2 )

имеет локальный минимум, а,

следова-

тельно, функция z = 8 - 2x - 4 y

в точке M 2 (2;2)

имеет условный мини-

мум

z(2;2) = -4 .

Замечание 1. Для функции трех переменных

u = f (x, y, z) , где пере-

менные связаны двумя уравнениями связи

j(x, y, z) = 0

y(x, y, z) = 0,

решение задачи на условный экстремум осуществляется следующим образом. 1. Строим функцию Лагранжа

F (x, y, z,l) = f (x, y, z) + l × j(x, y, z) + m × y(x, y, z) .

2. Строим систему уравнений для определения критических точек данной функции

∂f + λ ∂ϕ + μ			∂ψ = 0
	∂x	∂x	∂x
	∂f	+ λ ∂ϕ + μ	∂ψ = 0
	∂f	+ λ ∂ϕ + μ	∂ψ = 0
	∂y	∂y	∂y
	∂y	∂y	∂y
	∂f	∂ϕ	∂ψ
	∂z	+ λ ∂z + μ ∂z		= 0
	∂z	+ λ ∂z + μ ∂z		= 0
ϕ(x, y, z) = 0


ψ(x, y, z) = 0.
Решаем полученную систему уравнений, находим x, y, z,λ					и μ .
3. Для каждой полученной системы значений x, y, z					решаем отдель-
но вопрос о наличии в ней условного экстремума.

Пример 4. Найти условный экстремум функции u = x + y + z2 при

условиях связи

z − x −1 = 0

y − xz −1 = 0

Решение. Решим данную задачу, используя функцию Лагранжа. 1. Составим функцию Лагранжа

F (x, y, z,λ,μ) = x + y + z2 + λ(z − x −1) + μ( y − xz −1) .

2. Находим критические точки функции и для чего решаем систему уравнений

∂F = 1 − λ − μz = 0
	∂x
	∂F = 1 + μ = 0
	∂F = 1 + μ = 0
	∂y
	∂F
	∂F	= 2z + λ − μx = 0
	∂z	= 2z + λ − μx = 0
	∂z
	∂F	= z − x −1 = 0
	∂λ	= z − x −1 = 0
	∂F
	∂F	= y − xz −1	= 0
	∂μ	= y − xz −1	= 0


Решая систему уравнений получаем			x = −1, y = 1, z = 0, λ = 1, μ = −1,

т.е. M0 (−1,1,0) – единственная критическая точка функции u.

3. Проведем дополнительный анализ приращения функции u в

критической точке M0 (-1;	1; 0) . Пусть x0 удовлетворяет уравнениям свя-
зи, тогда имеем, что z0 =	1 + x0 , а y0 =1 + x0 (1 + x0 ) , т.е. координаты то-

чек, удовлетворяющих уравнениям связи M (x0 , 1 + x0 (1 + x0 ), 1 + x0 ) . То-

гда приращение функции

u = f (M ) − f (M 0 ) = x0 + 1 + x0 (1 + x0 ) + (1 + x0 )2 − (−1 −1) = 2(x0 + 1)2 > 0

для всех M ¹ M 0 . Следовательно, в точке M0 имеем минимум и

u(M0 ) = 0 .

Данную задачу можно решить и другим методом – методом исклю- чения или сведения данной задачи к исследованию на экстремум функции одной переменой. Действительно, решая уравнение связи относительно y

и z, находим y = x2 + x + 1 и z = x + 1, и, подставляя в исходную функ-

цию, получим функцию одной переменой x

u(x) = 2x2 + 4x + 2 = 2(x + 1)2 ,

которая имеет минимум при	x = −1, u(−1) = 0 .
Замечание 2. Отыскание условного экстремума функции z = f (x, y) ,
удовлетворяющего уравнению связи					ϕ(x, y) = 0 можно свести к исследо-
ванию на обычный экстремум функции Лагранжа
F (x, y,λ) = f (x, y) + λϕ(x, y) .
Нахождение необходимых условий (критические точки) условного
экстремума сводится к решению системы
∂F		=		∂f	+ λ	∂ϕ	= 0
	∂x			∂x		∂x
	∂F			∂f		∂ϕ
		=			+ λ		= 0
	∂y			∂y		∂y
	∂F		= ϕ(x, y) = 0.
	∂λ

Установление характера условного экстремума можно по знаку вто-
рого дифференциала функции		F (x, y,λ) , вычисленного для полученных

значений (x, y,λ) из системы уравнений, определяющих критические точ-

ки функции F (x, y,λ) , с учетом того, что		dx и dy связаны уравнением
∂ϕ dx +	∂ϕ dy = 0,	(dx2 + dy2 ¹ 0).
¶x	¶y
	85

А именно, если

d 2 F < 0 , то функция

f (x, y)

имеет условный мак-

симум; если d 2 F > 0

– условный минимум; если

d 2 F = 0 , то требуются

дополнительные исследования.

Пример

5. Исследовать

на условный

экстремум функцию

u = x2 + y2 + (z + 1)2 , если

x2 + y2 + z2 = 4 .

Решение. Составим функцию Лагранжа

F (x, y, z,λ) = x2 + y2 + (z + 1)2 + λ(x2 + y2 + z2 − 4) .

Приравнивая к нулю частные производные

F (x, y, z,λ) , получим

систему уравнений для нахождения критических точек.

∂F

= 2x + 2λx = 0

= 0

∂x

= 0

∂F

= 2 y + 2λy = 0

∂y

−1

∂F

+ λ

= 2(z + 1) + 2λz = 0

∂z

= 4

∂F

= x

+ y

+ z

− 4

= 0

(1 + λ)2

∂λ

Откуда имеем λ = −	1	,	λ		= −	3	и, соответственно, критические
				2
1	2				2

точки M1(0,0, −2), M 2 (0,0,2) .

Проверим выполнение достаточных условий экстремума. Так как смешанные частные производные функции F равны нулю, то

d 2 F (x, y, z,λ) =

∂2 F

dx2

∂2 F

dz2 =

∂x2

∂y

∂z

= 2(1 + λ)dx2 + 2(1 + λ)dy2 + 2(1 + λ)dz2 = 1(1 + λ)(dx2 + dy2 + dz2 ).

Так как dx2 + dy2 + dz2 > 0 , то знак

d 2 F

совпадает со знаком мно-

жителя (1 + λ) . Для точки M

имеем d 2 F (M

) = 1 > 0 , а для точки M

–

2 F (M

) = −1 < 0 , следовательно, функция u(x, y, z)

имеет в точке M

ус-

ловный минимум u(M1) = 1, а в точке

A2 –

условный максимум u( A2 ) = 9 .

§ 17. Наибольшее и наименьшее значения функции двух переменных в замкнутой области


Пусть функция	z = f (x, y) определена и непрерывна в ограничен-
ной замкнутой области	D и имеет в этой области конечные частные про-
изводные. По теореме Вейерштрасса (если функция		f (x, y) определена и
непрерывна в ограниченной замкнутой области D,		то m ≤ f (x, y) ≤ M ) в

этой области найдется точка (x0 , y0 ) , в которой функция принимает наи-

большее (наименьшее) значение. Если эта точка лежит внутри области D, то в ней функция имеет максимум (минимум) так что в этом случае инте- ресующая нас точка, наверное, содержится среди «подозрительных» по экстремуму стационарных (критических) точек. Но своего наибольшего (наименьшего) значения функция f (x, y) может достигать и на границе области. Таким образом, точки, в которых функция z = f (x, y) принимает

наибольшее и наименьшее значения, являются либо точками локального экстремума, либо граничными точками области D.

Значит, чтобы найти наибольшее и наименьшее значения функции z = f (x, y) в ограниченной замкнутой области D, следует вычислить зна-

чения функции в критических точках области D, а также наибольшее и наименьшее значения на ее границе.

Если граница области D задана уравнением ϕ(x, y) = 0 или не-

сколькими уравнениями такого же типа, и данное уравнение разрешимо относительно x или y, то задача нахождения наибольшего и наименьшего значений функции z = f (x, y) на границе области D приводится к нахож-

дению наибольшего и наименьшего значений функции одной переменной на отрезке.

Если граница области D задана параметрически: x = x(t) и y = y(t) или уравнением ϕ(x, y) = 0 , которое можно представить в пара-

метрическом виде, то, подставляя x(t) и y(t) в уравнение z = f (x, y) ,

приходим к выводу, что для нахождения наибольшего и наименьшего зна- чений функции z = f (x, y) на границе области D достаточно найти наи-

большее и наименьшее значения функции одной переменой t на отрезке. Если граница области D задана уравнением ϕ(x, y) = 0 , которое нельзя разрешить ни относительно x, ни относительно y, и также нельзя представить в параметрическом виде, то задача нахождения наибольшего и наименьшего значений функции z = f (x, y) на границе области D сводит-

ся к нахождению условного экстремума.

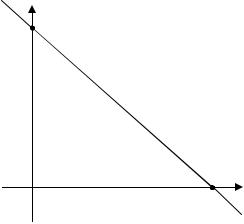
Пример 1. Найти наибольшее и наименьшее

значения

функции

z = x2 + 2xy − 3y2 + y

замкнутой

области

заданной неравенствами

0 ≤ x ≤ 1, 0 ≤ y ≤ 1, 0 ≤ x + y ≤ 1.

Решение.

Область

задания

функции D –

треугольник

АОВ.

Находим критические точки

x + y = 1

внутри области D:

∂z

= 2x

+ 2 y = 0

x = −

; y =

x = 0

∂x

∂z

∂y = 2x

− 6 y + 1 = 0

y = 0

−

1 1

Точка

;

не принад-

8 8

лежит области D, поэтому значение функции в этой точке не учитывается.

2. Исследуем функцию на экстремум на границе области D:

′

а) рассмотрим границу OA; y = 0; x [0;1] , тогда z = x ;

= 2x = 0;

x = 0 ,

следовательно

z1(0) = z(0;0) = 0; z2 (1) = z(1;0) = 1;

б) рассмотрим

границу

ОВ; x = 0; y [0;1] ,

тогда

z = −3y2 + y;

z′ y = −6 y + 1 = 0; y =

[0;1].

= z

;

z(0) = z(0,0) = z (0,0) = 0

z(0;1) = z4 (0,1) = −2 ;

x [0;1], а

в) рассмотрим границу ВА: x + y = 1, т.е.

y = 1 − x

z(x) = x2 + 2x(1 − x) − 3(1 − x)2 + (1 − x) = −4x2 + 7x − 2 .

Итак

z(x) = −4x

+ 7x − 2;

′

= −8x + 7;

′

= 0

при

x =

, y =

, x =

[0;1], поэтому

= z

;

8 8 16

z(0;1) = z4 (0;1) = −2;

z(1;0) = z2 (1;0) = 1.

3. Сравнивая полученные значения z1, z2 , z3 , z4

и z5 , получаем, что

7 1

наименьшее значение – z(0,1) = −2 , а наибольшее значение –

;

8 8

§ 18. Основные задачи и примеры для функции нескольких переменных

18.1.Топология плоскости

1.Описать геометрическое место точек на плоскости, удовлетво-

ряющих неравенству (x − 1)2 + ( y − 3)2 < 9 .

Решение. Так как (x − 1)2 + ( y − 3)2 – квадрат расстояния от точки

M (x, y) до точки O(1,3) , то данному неравенству удовлетворяют коорди-

наты точек, лежащих внутри окружности радиуса R = 3 , с центром в точке O(1,3) . Точки самой окружности (граница) не принадлежат искомому множеству. Данное множество является открытым связным множеством. В то же время это множество ограничено, но не является замкнутым, а, следовательно, данное множество не является компактом.

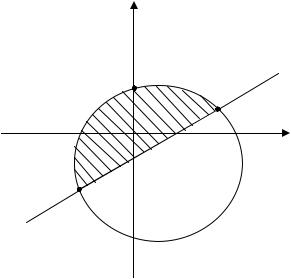
2. Описать геометрическое место точек плоскости, координаты ко- торых удовлетворяют системе неравенств:

(x − 4)2 + ( y + 2)2		≤ 25
	x − 2 y − 3 ≤ 0
	x − 2 y − 3 ≤ 0

Решение. Данной системе неравенств удовлетворяют коор- динаты точек кругового сектора

АМВ.

Данное множество является связным, ограниченным и замкну- тым, следовательно, компактным.


3. Пусть множество			А за-
дано неравенством		x2 + y2 ³1,
множество	В –	неравенством
x2 + y2 £ 4 , множество С –			нера-
венством	y ³ x2 , множество		D –

неравенством y £ 8 - x2 .

Описать следующие множества:

а) ( A È B) Ç (C È D) ;

в) ( A È B È C) Ç D ;

д) ( A È B È C) \ D .

B(7, 2)

M(4, –2)

A(–1, –2)

б)	( A Ç B) È (C È D) ;
г)	( A Ç B Ç C) È D ;

4. Доказать, что множество М, задаваемое системой неравенств:

+ y

+ z

>16 –

+ y

£16

а) x

открыто;

б) x

– замкнуто;

x + 3y - 2z > 6

x + 3y - 2z £

+ y

+ z

³ 25 –

в) x

не является ни открытым, ни замкнутым.

x + 3y - 2z > 6

Найти предельные точки множества М, не принадлежащие этому множеству.

Найти точки множества М, не являющиеся внутренними.

18.2. Функция двух (нескольких) переменных

1. Найти и изобразить область определения функции:

z =

x2 + y

z =

а)

;

б)

y sin x ;

x2 - y2

в)

z = arccos(x2 + y2 ) ;

г)

z = arcsin

+ arcsin(1 − y) ;

u =

u = arcsin x + arcsin y + arcsin z .

д)

z ;

е)

Ответы:

а)

;

б) если

y ³ 0 , то

2pn £ x £ (2n +1)p;

если

y £ 0

, то (2n +1)p £ x £ (2n + 2)p; n Î z ;

в)

x2 + y2 ≤ 1;

г)

криволинейный треугольник, ограниченный параболами y2 = x,

y2 = −x и прямой

y = 2 вместе с точками границы, кроме (0,0);

д)

первый октант (включая границу);

е) куб, ограниченный плоскостями

x = ±1, y = ±1, z = ±1, включая

его грань.

z = f (x, y)

Замечание. Линия уровня функции

на плоскости – это

такая

линия,

в которой функция

принимает одно и то же значение

z = c

( f (x, y) = c) .

Поверхность

уровня

функции

трех переменных

u = f (x, y, z) такая поверхность

f (x, y, z) = c ,

в точках которой принимает

постоянное значение

u = c .

2. Найти линии уровня функции и выяснить характер (вид) поверхностей:

а) z = xy ;

б) z = x + y ;

в) z = x2 + y2 ;

г) z = x2 − y2 ;

д) z =

;

е) z = (1 + x + y)2 .

<<< < Предыдущая 1 2 3 4 5 6 7 89 / 369 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

Соседние файлы в папке Высшая математика (РТФ)

#
18.05.20154.76 Mб33умк_Вакульчик_Элементы векторной алгебры.pdf
#
18.05.20155.38 Mб38умк_Вакульчик_Элементы линейной алгебры.pdf
#
18.05.20151.33 Mб40умк_Мальцев_Осн дискретной матем.pdf
#
18.05.20153.75 Mб39умк_Пальчик_Теория вероятностей.pdf
#
18.05.20155.68 Mб32умк_Цывис_Диф.уравнения_Ряды.pdf
#
18.05.20154.7 Mб39умк_Цывис_Функции_Интеграл. исчисл..pdf
#
18.05.20153.54 Mб76умк_Яско_ Диф.уравнения_Ряды.pdf