Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Пензенский Государственный Университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

умк_Цывис_Функции_Интеграл. исчисл

..pdf

Скачиваний:

Добавлен:

18.05.2015

Размер:

4.7 Mб

Скачать

☆

<<< < Предыдущая 4 5 6 7 8 9 10 11 12 13 14 1516 / 3616 17 18 19 20 21 22 23 24 25 26 27 28 > Следующая >>>

части (14), то знаменатели этого тождества одинаковы, а, следовательно, и числители должны быть тождественно равны между собой. После приве- дения подобных в числителе правой части (14), приравнивая коэффици- енты при одинаковых степенях числителей полученного тождества, полу-

чим совместную систему линейных уравнений			относительно				Ai и
Bi (i =		) . Решая ее, определим коэффициенты	Ai и Bi (i =			) , а, сле-
	1, n				1, n
довательно, и разложение дроби (14) на простейшие.
Пример 7. Найти разложение дроби на простейшие				3x2 + 5x +12
								.
				(x2 + 3)(x			2 +1)

Решение. Знаменатель правильной дроби не имеет действительных кор- ней, поэтому разложение на простейшие имеет вид

3x2 + 5x +12	=	Ax + B	+	Cx + D
					.
(x2 + 3)(x2 +1)		x2 + 3
				x2 +1

Приводя к общему знаменателю правую часть последнего тождества и приравнивая числители, получим тождество

3x2 + 5x +12 º ( A + C)x3 + (B + D)x2 + ( A + 3C)x + (B + 3D)

Откуда, приравнивая коэффициенты при одинаковых степенях, по- лучим совместную систему

			A + C = 0

	B + D = 3								,
			A + 3C = 5						,
	B + 3D =12
решая которую, получим A = -		5	, B = -				3	,		C =			5		,	D =	9	.
решая которую, получим A = -			, B = -					,		C =			2		,	D =		.
2						2							2			2
А разложение будет иметь вид
	3x2 + 5x +12		= -	1	×	5x + 3				+	1	×		5x + 9

	(x2 + 3)(x2 +1)			2		x2 + 3					2			x2		+1
	(x2 + 3)(x2 +1)			2		x2 + 3					2			x2		+1

3. Пусть правильная несократимая дробь F (x) такова, что

Q(x)

Q(x) = (x - x1)(x - x2 )k ...(x - xn )

151

знаменатель имеет действительные различные корни, среди которых име-

ются кратные корни, тогда разложение дроби

F (x)

имеет вид

Q(x)

F (x)

− x1 )(x − x2 )k

x − x1

x − x2

Q(x) (x

...(x − xn )

(15)

+ ... +

(x − x2 )2

(x − x2 )3

(x − x2 )k

x − xn

Для определения коэффициентов в разложении (15) поступают ана- логично, как в случае 2.

Пример 8. Найти разложение дроби на простейшие дроби	2x2 − 3x + 3
		.
	x3 − 2x2 + x

Решение. Данная дробь правильная, знаменатель которой имеет действи-

тельные корни, но среди них есть кратные x3 − 2x2 + x = x(x −1)2 . Следо-

вательно, разложение на простейшие дроби имеет вид

	2x2 − 3x + 3	=	2x2 − 3x + 3	=	A	+	D	+	B	.
	x3 − 2x2 + x		x(x −1)2						(x −1)2
					x (x −1)
После тождественных преобразований получим тождество
	2x2 − 3x + 3 ≡ ( A + D)x2 + (−2 A − D + B)x + A .									(16)

Находить коэффициенты можно, как и выше, приравнивая коэффи- циенты при одинаковых степенях и решая совместную систему уравнений.

Несколько проще можно определить коэффициенты A, D, B в тож- дестве (16), полагая x1 = 0, x2 = 1 (корни знаменателя), а x3 – любое число.

X = 0, тогда A = 3; x = 1, тогда B = 2; при x = 2 получим 5 = A + 2B + 2D или 2D = – 2, т.е. D = –1.

Тогда разложение имеет вид

2x2 − 3x + 3

−

x3 − 2x2 + x

x(x −1)2

x x −1 (x −1)2

4. Пусть правильная несократимая дробь

F (x)

такова

Q(x)

152

Q(x) = (x2 + p x + q )(x2

+ p x + q )k ...(x2 + p x + q ) ,

что знаменатель имеет комплексные корни,

среди которых есть кратные,

тогда разложение дроби

F (x)

имеет вид

Q(x)

F (x)

Q(x) (x2

+ p1x + q1 )(x2 + p2 x + q2 )k ...(x2 + pn x + qn )

A1x + B1

M1x + N1

M 2 x + N2

+ +

+ ...

(17)

x2 + p x + q

(x2 + p x + q )2

M n x + Nn

+ ... +

An x + Bn

(x2 + p x + q )k

(x2 + p x + q )n

Коэффициенты в разложении

(17)

определяем как в случае 3, т.е.

решением совместной системы линейных уравнений.

Пример 9. Найти разложение дроби на простейшие дроби

x4 + 2x2 + 4

(1 + x2 )3

Решение. Знаменатель данной дроби имеет два линейных корня

x = ±i

кратности 3. Поэтому разложение имеет вид

x4 + 2x2 + 4

A x + B

A x

A x + B

(1 + x2 )3

(1 + x2 )2

1 + x2

(1 + x2 )3

Используя один из рассмотренных методов определения коэффициентов,

получим, что A0 = 0, B1 = 1, A2		= 0,		B2 = 0,		A3 = 0,			B2 = 3 , а, следователь-
но, разложение имеет вид
	x4 + 2x2 + 4		=	3	+		1		.
	(1 + x2 )3			(1 + x2 )3			+ x2
					1
Если правильная рациональная дробь						F (x)		такова, что знаменатель

						Q(x)

Q(x) имеет корни как действительные, так и комплексные, среди которых

могут быть и кратные, то разложение дроби F (x) на простейшие прово-

Q(x)

дим, используя рассмотренные выше случаи 1 – 4.

153

3.4. Интегрирование рациональных дробей

Для нахождения интеграла

	∫	Pm (x)	dx ,				(1)
	∫		dx ,				(1)
		Q (x)
		n
где Pm (x) ,	Qn (x) многочлены с действительными коэффициентами
				Pm	(x)
степени m и	n соответственно и		m < n, т.е.			–	правильная ра-
степени m и	n соответственно и		m < n, т.е.			–	правильная ра-
				Qn (x)

циональная дробь, то ее можно представить в виде суммы простых дро- бей вида

A	,	Bx + D	, k, s N , p	2	− 4q < 0 .	(2)
(x − a)k		(x2 + px + q)s

Если Pm (x) – дробь неправильная (m ³ n) , то, разделив числитель на зна-

Qn (x)

менатель, получим

		Pm (x)		= S (x) +		R(x)
							,	(3)
		Qn (x)
					Qn (x)
где S(x) – многочлен (частное от деления						Pm (x) на Qn (x) ), R(x) –		оста-
ток от деления, причем	R(x)		–	правильная дробь. Таким образом,				интег-

	Qn (x)

рирование рациональной функции сводится к интегрированию многочлена

S(x) и правильной дроби R(x) в равенстве (3).

Qn (x)

Для интегрирования правильной дроби R(x) используем разложе-

Qn (x)

ния на простейшие рациональные дроби вида (2), рассмотренные в п. 3.3. Рассмотрим примеры интегрирования рациональных функций.

Пример 10. Найти интеграл I = ∫			x	4	dx .


	x	2	− x + 1

Решение. Так как подынтегральная дробь неправильная, но, выполнив де- ление, получим

x	4	= x 2 + x −	x	= x	2	+ x −	1 (2x − 1)	−	1		1			.

			x 2 − x + 1				2 x 2 − x + 1		2		1 2
x 2 − x + 1			x 2 − x + 1				2 x 2 − x + 1		2		1 2		3
										x −		+
										x −		+	4
											2		4

154

2x − 1

Тогда I =

−

ln(x2

− x + 1) −

arctg

+ C .

Пример 11. Найти интеграл I = ∫

3x + 1

dx .

x(1 + x2 )2

Решение. Подынтегральное выражение – правильная рациональная дробь, разложение которой на простейшие имеет следующий вид

3x + 1

Bx + C

Dx + F

x(1 + x 2 )2

1 + x 2

(1 + x 2 )2

После приведения к общему знаменателю в правой части равенства и

приравнивая числители, получим

3x + 1 = ( A + B)x 4 + Cx3 + (2 A + B + D)x 2 + (C + F )x + A .

Приравнивая коэффициенты при одинаковых степенях

в послед-

нем тождестве, и решая совместную систему относительно А, В, С, D и F

получим A = 1,

B = –1,

C = 0,

D = –1,

F = 3. Тогда

I = ∫

3x + 1

∫

− ∫

xdx

− ∫

xdx

+3∫

x(1 + x2 )2

+ x2

+ x2 )2

(1 + x2 )3

= ln

−

ln(1

+ x2 ) − −

∫

d (1 + x2 )

+ 3I1

= ln

−

ln(1

+ x2 ) +

+ 3I1.

(1 + x2 )2

2 (1 + x2 )

(1 + x2 ) − x2

xd (1 + x2 )

= ∫

dx =

∫

−

∫

(1 + x2 )2

1 + x2

(1 + x2 )2

= arctgx −

xd (1 + x2 )

u = x

du = dx

∫

d υ =

d (1

+ x2 )

υ =

−1

+ x2 )2

(1 + x2 )2

1 + x2

= arctgx −

−x

+ ∫

= arctgx +

−

arctgx

+ x

2(1 + x

)

2(1 + x

)

Тогда искомый интеграл I будет равен

I = ln

−

ln(1 + x2 ) +

3x + 1

arctgx + C.

2(1 + x2 )

Пример 12. Вычислить интеграл

I = ∫

x(3 + x 4 )2

155

Решение.

(3 + x6 ) − x6

x5dx

I =

∫

dx =

∫

−

∫

x(3 + x6 )2

x(3 + x6 )

(3 + x6 )2

d (

+1)

d (3 + x6 )

= -

∫

= -

1 +

+ C .

×18

3 ×

(3 + x6 )2

18(3 + x6 )

Пример 13. Вычислить интеграл

I = ∫

(x 2 +1)(x 2 + 4)

Решение. Знаменатель подынтегральной дроби имеет две пары различных комплексных сопряженных корней, поэтому разложение имеет вид

1	=	Ax + B	+	Dx + E	.
(x 2 +1)(x 2 + 4)
		x 2 +1 x 2 + 4

Откуда имеем тождество 1 º ( Ax + B)(x 2 + 4) + (Dx + E)(x 2 +1) .

Можно построить систему линейных уравнений и найти их решение (четыре уравнения и четыре неизвестных). Но удобнее применить метод частных значений с использованием комплексных чисел – корней знамена-

теля x = ±i, x = ±2i .
Полагая x = i, получим 3B + 3Ai = 1, т.е. A = 0,											B =		1		.
Полагая x = i, получим 3B + 3Ai = 1, т.е. A = 0,											B =				.
											3
Полагая x = 2i, получим –3 E – 6 Di = 1, т.е. D = 0, E + -																1	.
Полагая x = 2i, получим –3 E – 6 Di = 1, т.е. D = 0, E + -																	.
											3
Таким образом, I =	1	∫	dx	-	1	∫	dx	=	1	arctgx -		1		arctg				x	+ C .
Таким образом, I =		∫	x2 +1	-		∫	x2 + 4	=		arctgx -				arctg					+ C .
3			x2 +1	3			x2 + 4	3			6							6

Замечание 1. Рассмотренный пример разобран с точки зрения разло- жения на простейшие дроби для того, чтобы показать, что находить коэф- фициенты разложения можно, используя и множество комплексных чисел, и довольно успешно.

Замечание 2. Интегралы данного вида находят значительно проще, а именно

1	=	1		1	-	1

(x2 +1)(x2 + 4)		3
			x2 +1			x2 + 4

откуда получаем табличные интегралы.

156

Пример 14. Вычислить интеграл	I = ∫			dx	.

Решение. В силу равенства			x	4 + 1

x4 + 1 = (x4 + 2x2 + 1) − 2x2 = (x2 + 1)2 − (		)2 = (x2 +					x + 1)(x2 −		x + 1)
	2x					2		2

и, учитывая, что для каждого квадратичного трехчлена D < 0, получим разложение

1	=	Bx + D			+	B1x + D1
									.
x4 +1		x2 +		x +1		x2 -		x +1
			2				2

Откуда имеем тождество


1 = (Bx + D)(x2 −	2	x + 1) + (B x + D )(x2		+	2	x + 1) .	(4)
1			1

Приравнивая коэффициенты при одинаковых степенях переменной х, получим совместную систему линейных уравнений

0 = B + B1

0 = -B2 + D + B1 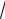2 + D1

0 = B - 2D + B1 + 2D1

1 = D + D1

Решая которую, находим

		B =	1		,		D =			1	,	B = -				1		,		D =	1	.


			2	2					2			1			2	2			1		2
			2	2					2						2	2					2

		1		1					x + 2						x -		2
Тогда		1	=	1		×			x + 2				-		x -		2			.
Тогда			=			×							-							.
	x	4 + 1 2 2 x						2	+ x 2 + 1 x					2	- x 2 + 1

Следовательно

											d (x +			1		)
			(x + 2)		1		2x + 2		1
														2
														2
I1	= ∫			dx =		∫		dx +		∫								=
												1
		x	2 + x 2 + 1		2				2					2
		x	2 + x 2 + 1		2		x2 + x 2 + 1		2		(x +		)	2	+		1
																	2
												2
												2

=1 ln(x2 + x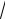2 + 1) + arctg(x2 + 1) + C1. 2

(x -

= ∫

2)dx

ln(x2 - x

+ 1) - arctg(x

-1) + C2 , то

x2 - x

2 + 1

x2 + x

+ 1

I =

(I1 + I2 ) = ∫

x4 + 1

2 2

4 2 x2 - x 2 + 1

´(arctg(x

+1)

- arctg(x

-1) + C.

157

Замечание 3. Приведем другой способ вычисления коэффициентов B,

D, B , D в разложении (4). Корни многочлена

x4 + 1 определяются фор-

π+2kπ i

xk = e

мулой

где k = 0, 1, 2, 3.

= ei 4 =

(1 + i)

трехчлена x2 +

x + 1, а

При

этом x

–

корень

x = x

= −x

корень трехчлена x2 −

x + 1.

–

x = x0 и сравнивая в полученном соотношении дейст-

Полагая в (4)

вительные и мнимые части находим

и D1 . Таким же образом, полагая

в (4)

x = −x0 найдем B и D.

Замечание 4. В некоторых случаях для вычисления интегралов от ра- циональной дроби целесообразно, вместо разложения ее на простейшие дроби применить другой метод – преобразование дроби, использование подходящей подстановки или метод интегрирования по частям.

Пример 15. Вычислить интегралы

I1 = ∫

2 =

∫

+ 1

= ∫

15.1.

dx ;

15.2.

dx ;

15.3. I3

(x −1)5

+ 1

(1 + x2 )

Решение.

(x − 1)2 + 2(x − 1) + 1

15.1.

I1 = ∫

dx =

∫

dx =

(x − 1)5

= −

−

+ C

2 (x − 1)2

3(x − 1)3

4(x −

1)4

+ 1

1 +

d (x −

)

dx = ∫

= ∫

15.2. I2 = ∫ x4 + 1

(x −

)

+ 2

x −

2 − 1

arctg

+ C =

arctg

+ C.

15.3. Так как

I = ∫R(sin x,

cos x)dx .

Тогда

I3 = ∫

= −

+ arctgx + C .

3x2

4 (1 + x2 )

158

§ 4. Интегрирование выражений, содержащих тригонометрические функции

Суть интегрирования выражений, содержащих тригонометрические функции, состоит в следующем: с помощью подходящей замены перемен- ной или подстановки интегрирование выражений, содержащих тригоно- метрические функции, приводятся к интегрированию рациональных или дробно-рациональных функций.

4.1 Интегрирование дифференциалов R(sin x, cos x)dx

Вычисление интегралов вида

I = ∫R(sin x, cos x)dx

сводится к вы-

числению

интегралов

от

рациональной

функции

подстановкой

t = tg

(−π < x < π) ,

которая называется универсальной тригонометриче-

ской подстановкой.

Действительно, в силу того,

что

2tg

1 − tg2

1 − t 2

sin x =

;

cos x =

;

2 x

+ t

2 x

1 + t 2

1 + tg

2dt

1 − t 2

2dt

x = 2arg tg t :

dx =

тогда R(sin x,

cos x)dx = R

+ t 2

1 + t 2

1 + t2

Таким образом, интегралы вида

I = ∫R(sin x,

cos x)dx =

1 − t

2dt

∫R

(1)

1 + t

2 1 + t2

всегда берутся в конечном виде.

Отметим, что если функция R(sin x, cos x) линейная относительно sin x и cos x (содержит выражения sin x и cos x в первой степени), то уни-

версальная тригонометрическая подстановка (t = tg x ) приводит к эффек- 2

тивному вычислению интегралов вида (1). Если же функция R(sin x, cos x) содержит выражения sin x и cos x в высоких степенях, то универсальная

тригонометрическая подстановка t = tg x приводит к слишком громоздким

выкладкам, но всегда интегралы вида (1) берутся в конечном виде.

159

Пример 1.

Найти интеграл

I = ∫

(1 + sin x)dx

sin x(1 + cos x)

Решение.

(1 + sin x)dx

t = tg

: x = 2arctg t

I = ∫

sin x(1 + cos x)

dx =

2dt

: sin x

: cos x =

1 − t 2

+ t 2

+ t

1 + t2


	(1 +		2t	)		2dt
			+ t 2
= ∫	1				1 + t2			=
		2t	(1 +		1	− t2	)
	1 + t 2
				1		+ t 2

(t 2 + 2t + 1)dt

2 x

∫

(

+ 2t + ln

) + C =

+ tg

+ C.

2 2

Пример 2.

Найти интеграл I = ∫

sin x

Решение. Используя универсальную тригонометрическую подстановку

(t = tg

I = ∫

(1 + t2 )2dt

= ∫

= ln

+ C = ln

+ C.

) , получим

2t(1 + t 2 )

Пример 3.

Найти интеграл

I = ∫

cos x

Решение. Этот интеграл можно найти, используя универсальную тригоно-

метрическую подстановку (t = tg x ) , или свести к нахождению интеграла в

примере 2.

d (x + π)

tg(x + π)

Действительно, I = ∫

= ∫

= ln

+ C .

sin(x + π)

cos x

Приведем другой способ вычисления интегралов I = ∫

;

I = ∫

sin x

cos x

Пример 4.

Найти интеграл I = ∫

sin x

1 − cos x

Решение. I = ∫

= ∫

sin dx

= ∫

d (cos x)

+ C .

sin x

cos2 x −1

sin2 x

1 + cos x

Ниже рассмотрим случаи вычисления интегралов, содержащих три- гонометрические функции и дающих результаты эффективнее, чем ис- пользование универсальной тригонометрической подстановки. Предвари- тельно сделаем следующие замечания из алгебры.

160

<<< < Предыдущая 4 5 6 7 8 9 10 11 12 13 14 1516 / 3616 17 18 19 20 21 22 23 24 25 26 27 28 > Следующая >>>

Соседние файлы в папке Высшая математика (РТФ)

#
18.05.20154.76 Mб33умк_Вакульчик_Элементы векторной алгебры.pdf
#
18.05.20155.38 Mб38умк_Вакульчик_Элементы линейной алгебры.pdf
#
18.05.20151.33 Mб40умк_Мальцев_Осн дискретной матем.pdf
#
18.05.20153.75 Mб39умк_Пальчик_Теория вероятностей.pdf
#
18.05.20155.68 Mб32умк_Цывис_Диф.уравнения_Ряды.pdf
#
18.05.20154.7 Mб39умк_Цывис_Функции_Интеграл. исчисл..pdf
#
18.05.20153.54 Mб76умк_Яско_ Диф.уравнения_Ряды.pdf