умк_Цывис_Функции_Интеграл. исчисл

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Пензенский Государственный Университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

I = ∫sin4 x cos5 x dx = ∫(t4 - 2t6 + t8 )dt =

Замечание 4. Интеграл I = ∫sin4 x cos5 x dx

можно найти следую-

щим образом

..pdf

Скачиваний:

Добавлен:

18.05.2015

Размер:

4.7 Mб

Скачать

☆

<<< < Предыдущая 5 6 7 8 9 10 11 12 13 14 15 1617 / 3617 18 19 20 21 22 23 24 25 26 27 28 29 > Следующая >>>

Замечание 1. Если целая или дробно-рациональная функция R(u, g) не меняет своего значения при изменении знака одного из аргументов, на- пример u, т.е., если R(– u, g) = R(u, g), то она может быть приведена к виду

R(u, g) = R1(u2, g),	содержащему лишь четные степени u.
Замечание 2.	Если целая или дробно-рациональная функция R(u, g)

при изменении знака одного из аргументов также меняет знак, т.е., если R(– u, g) = – R(u, g), то она приводится к виду R(u, g) = R2(u2, g)·g; это следу-

ет из предыдущего замечания, если его применить к функции		R(u, g)	.
ет из предыдущего замечания, если его применить к функции			.
		u
Рассмотрим интеграл
I = ∫R(sin x, cos x)dx .	(1)
Тогда
I. Если R(u, g) меняет знак при изменении u, тогда
R(sin x, cos x)dx = R0(sin2 x, cos x)sin x·dx = – R0(1–cos 2x, cos x)d·cos x,
т.е., если
R(–sin x, cos x) = –(sin x, cos x),
то интеграл (1) приводим к интегрированию рациональной функции от-
носительно переменной t, с помощью подстановки t = cos x,	x (0;π) .
II. Если R(u, g) меняет знак при изменении знака g, то

R(sin x, cos x)dx = R1(sin x, cos2x)cos x·dx = R1(sin x, (1 – sin 2x)dx,

т.е., если

R(sinx, –cos x) = – R(sinx, cosx),

то интеграл (1) приводим к интегрированию рациональной функции отно-

сительно переменной t, с помощью подстановки t = sin x,

x Î(- π : π ).

III. Если, R(u, g) не меняет своего значения при одновременном из-

менении знаков u и g.

R(-u, -g) = R(u, g) = R(

× g, g) = R (

, g) = R (

, g2 ) .

Поэтому R(sin x, cos x) = R (tgx, cos

2 x) = R

= R(tgx) , а сле-

tgx,

1 + tg2 x

довательно интеграл (1) приводим к интегрированию рациональной функ-

ции относительно					переменной t, с	помощью подстановки
		p	p			dt

t = tgx : x Î	-	:		,	ибо R(sin x,cos x)dx = R(t)		.
						1 + t 2
		2	2

161

Замечание 3. Отметим, что, какова бы не была рациональная функ- ция R(u, g), ее всегда можно представить в виде суммы трех слагаемых, рассмотренных выше, т.е.

R(u, g) = R(u, g) − R(−u, g) + R(−u, g) − R(−u, −g) + R(−u, −g) + R(u, g) . (2)

В равенстве (2) первое слагаемое меняет знак при изменении знака

u, второе меняет знак при изменении знака

g, а третье сохраняет значение

при одновременном изменении знаков

и g. Поэтому, представив выра-

жение

R(sin x, cos x) в виде

(2), к первому слагаемому применим подста-

новку

t = cos x t, ко второму –

подстановку t = sin x , и к третьему – t = tgx .

Следовательно, для вычисления интегралов вида (1) достаточно трех

подстановок.

Пример 5. Найти интеграл

I =

∫

cos x + cos3 x

dx .

1 + sin2 x

Решение. Функция R(sin x,cos x) =

cos x + cos3 x

нечетная

относительно

1 + sin2 x

cos x , поэтому t = sinx : dt = cos x·dx,

а следовательно

I = ∫

(1 + cos2 x)cos xdx

= ∫

(2 − sin2 x)cos xdx

= ∫

2 − t

dt =

1 + sin2 x

1 + t

= −∫dt + 3∫1 +dtt 2 = −sin x + 3arctg sin x + C

4.2. Интегралы вида Im,n = ∫sinm x cosu x dx .

При нахождении интегралов вида Im,n применяют следующие правила:

1.n – целое положительное нечетное число, то применяется подста- новка t = sin x.

2.m – целое положительное нечетное число, то применяется подста- новка t = cos x.

3. m + n –	четное целое число, то применяются			подстановки либо
t = tg x, либо t = cos2x.
Пример 6.	Найти интеграл I4,5 = ∫sin4 x cos5 x dx .
			1dt
Решение. Используем подстановку t = sin x, тогда dx =			1dt		; cos x = 1 − t 2 .


		1 − t2

162

Следовательно,


I4,5 = ∫sin4 x cos4 x cos x dx = ∫sin4 x cos4 x d sin x = ∫sin4 x × (1 - sin2 x)2 d sin x =
= ∫sin4 x(1 - 2sin2 x + sin4 x)d sin x =			sin9 x		-	2	sin7 x +	sin5 x	+ C
= ∫sin4 x(1 - 2sin2 x + sin4 x)d sin x =					-		sin7 x +		+ C
		9			7		5
Пример 7. Найти I = ∫		dx
				.
	sin			.
	sin	2 x × cos4 x

Решение. Данный интеграл можно найти, используя подстановку tg x = t, 2

но проще найти данный интеграл преобразованием подынтегральной функции, используя основное тригонометрическое тождество («разбиение единицы») sin2x + cos2x = 1 или соответствующую степень тригонометри- ческой единицы. В данном примере можно использовать равенство

1 = sin2x + cos2x,

но эффективнее будет I 2 = (sin 2 x + cos2 x)2 ,получим

I sin2

x + cos2 x)2

(sin4 x + 2sin2 x cos2 x + cos4 x)

I = ∫

dx = ∫

dx =

sin

2 x cos4 x

sin2

x cos4 x

sin2 x

= ∫

dx + 2∫

+ ∫

cos

sin

= ∫tg2 x dtgx + 2tgx - ctgx =

tg3 x

+ 2tgx - ctgx + C.

Замечание

5. При вычислении интегралов вида I = ∫

1× dx

sin

x cos

удобно использовать «разбиение единицы» (1 = sin2x + cos2x) или соответ- ствующую степень тригонометрической единицы.

Замечание 6. Интегралы вида I = ∫sin p x cosg x dx (p и g – рацио-

нальные числа, x Î(0 : π) ) подстановкой sin x = t приводятся к интегралу

от биномиального дифференциала

I = ∫sin p x cosg x dx = ∫t p (1 - t2 )g −1dt .

163

4.3. Интегралы вида	In = ∫tgn x dx,	In = ∫ctgn x dx
Для нахождения интеграла	In = ∫tgn x dx	поступают следующим об-
разом (n ≥ 2)

In = ∫tgn x dx = ∫tg2 x × tgn − 2 x dx = ∫( cos12 x -1)tgn − 2 x dx =

= ∫tgn − 2 x dtgx - ∫tgn − 2 x dx,

= tgn−1x -

т.е. In - In−2 – рекуррентное соотношение. n 1

Аналогично находим интеграл In = ∫ctgn xdx .

4.4. Интегралы вида

I = ∫sin ax × cosbx × dx , I = ∫cos ax × cosbx , I = sin ax ×sin bx

Интегралы вида

I = ∫sin ax × cosbx × dx , I = cos ax × cosbx × dx , I = ∫sin ax ×sin bx × dx

находим преобразованием произведения тригонометрических функций в сумму или разность, пользуясь одной из следующих формул:

2sin ax · cos bx = sin(a – b)x + sin(a + b)x;

2cos ax · cos bx = cos(a – b)x + cos(a + b)x;

2sin ax · sin bx = cos(a – b)x – cos( a + b)x.

Пример 8. Найти интеграл I = ∫sin ax × cosbx × dx .

Решение. I = ∫sin ax × cosbx × dx = 12 ∫[sin(a - b)x × dx + sin(a + b)x]dx =

= -	1	cos(a - b)x		+	cos(a + b)x	+ C.

	2		a - b		a + b

164

§5. Интегрирование выражений, содержащих радикалы

Основной прием интегрирования выражений, содержащих радикалы, – нахождение таких подстановок t = ϕ(t) ( ϕ(t) – выражается через элемен-

тарные функции), которые привели бы подынтегральное выражение к ра-

циональному виду, так называемый метод рационализации подынтеграль- ного выражения.

5.1. Интегрирование функций вида		ax + b
	R x, n

		cx + d

Пусть

ax + b

I = ∫R x, n

dx ,

(1)

cx + d

где

R – рациональная функция от двух аргументов;

n –

натуральное чис-

ло;

a, b, c, d – постоянные числа.

Для нахождения интеграла (1)

положим

ax + b

dt n − b

ax + b

= t; t

cx + d

= cx + d ;

x = ϕ(t) = a − ct n

тогда интеграл (1) примет вид

′

(2)

∫R(ϕ(t),t)ϕ (t)dt ,

где дифференциал имеет рациональный вид, так как

′

ра-

R(t), ϕ(t), ϕ (t) –

циональные функции от

t, а, следовательно, интеграл (2) находится в ко-

нечном виде и, тем самым, находим интеграл (1).

К интегралу вида (1) сводятся и более общие интегралы

		ax + b
∫R x,		ax + b
∫R x,
	cx + d

где ns ÎQ(s =1, k ); a, b, c, d Î R, ad - bc ¹ 0 ,

подстановкой ax + b = t p , где p – общий знаменатель чисел n1, n2, …, nk, cx + d

приводятся к интегралам от рациональных функций.

165

Пример 1.

Найти интеграл

I = ∫ 3

x +1

x -1

x +1

6t 2dt

Решение.

t = 3

x +1

x =

dx = -

Пусть

;

(t3 -

1)2

x -1

-1

I = -3

-1

t + 2

dt =

t2 + t +1

arctg

+ C ,

тогда

∫

3 -1

t 2 + t

(t -1)2

t -1

где

t = 3

x +1

x -1

Пример 2.

I = ∫

x + x

+ x

dx .

Найти интеграл

x(1 + x

)

Решение. Наименьшее общее кратное знаменателей (1; 3; 6) равно числу 6,

поэтому применим подстановку x = t6;

dx = 6t5dt , тогда

(t6

+ t4

+ t)t5dt

+ t3

I = 6∫

= 6∫

dt = 6∫(t

)dt =

+ 6arctgt + C ,

t6 (1

+ t2 )

t 2 +

где x = t6.

5.2. Интегрирование функций вида R(x, ax2 + bx + c )

Интегралы вида

I = ∫R(x, ax2 + bx + c )dx, a ¹ 0; b2 - 4ac ¹ 0 .

(1)

Сводятся к интегрированию рациональных функций с помощью под- становок Эйлера:

	ax2 + bx + c = ±t ±				a > 0 ,
1)	ax2 + bx + c = ±t ±		a x,		a > 0 ,	(2)

		ax2 + bx + c = ± xt ±			c > 0 ,
2)		ax2 + bx + c = ± xt ±		c ,	c > 0 ,	(3)

3) ax2 + bx + c = ±t(x − α), b2 − 4ac > 0 ,

(4)

где a – один из корней квадратного трехчлена ax2 + bx + c.

166

Действительно, например, в первой подстановке Эйлера формула (2) положим

ax2 + bx + c = t −

x, a > 0 .

(5)

Возводя равенство (5) в квадрат получим

− c

+ bt + c

at 2

x =

;

ax2 + bx + c =

2 at + b

at + b

dx = 2 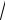at 2 + bt + c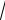a dt . (2at + b)2

Суть подстановки Эйлера состоит в том, что для определения x по-

лучается уравнение первой степени, таким образом, что х и 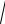ax2 + bx + c , выражаются рационально через t. Таким образом, первая подстановка Эй- лера (2) сводит интеграл (1) к интегрированию рациональной функции от t.

Вторая подстановка Эйлера (3), например,

ax2 + bx + c = xt +

c > 0 . После возведения в квадрат и

приведения

подобных, получим

ax + b = xt2 + 2

– уравнение первой степени относительно х. Откуда

ct − b

ct 2 − bt + a c

ct2 − bt + a c

x =

;

ax2 + bx + c =

; dx = 2

dt ,

a − t2

a − t

(a − t 2 )2

а, следовательно, интеграл (1) сводится к интегрированию рациональной функции от t.

Замечание 1. Рассмотренные выше первая и вторая подстановки (а > 0

и c > 0) приводятся одна к другой подстановкой x = 1 . Следовательно, t

всегда можно избежать применения второй подстановки.

Третья подстановка применяется в том случае, если квадратный трехчлен ax2 + bx + c имеет различные действительные корни α и β, т.е.

ax2 + bx + c = a( x − α)( x − β) .

Положим

ax2 + bx + c = t( x − α) , после возведения в квадрат и со-

кращая на

(х –

α) получим и здесь уравнение первой степени относитель-

αt2

− aβ

a(α − β)t

2a(β − α)t

но х, так

что

x =

; ax2 + bx + c =

; dx =

dt , а

t2 − a2

t 2 − a2

(t 2 − a)2

следовательно интеграл (1) сводится к интегрированию рациональной функции от t.

167

= (x − α) a

x − β

ax2 + bx + c

Замечание 2.

При

a(x − α)(x − β)

x − α

x − β

интеграл I = ∫R(x,

ax2 + bx + c )dx = ∫R(x, (x − α) a

dx сводится

x − α

интегрированию рациональной функции с помощью подстановки t = a

x − β

x − α

Пример 3. Найти интеграл I = ∫

, используя подстановки Эйлера.

1 − x2

Решение. а) интеграл I = ∫

= arcsin x + C – табличный интеграл;

1 − x2

b) для нахождения

I = ∫

применим третью подстановку Эйлера:

1 − x2

2 −1

2dt

4tdt

1 − x2 = t(1 − x) , тогда x =

;

1 − x2 =

;dx =

(t2 + 1)2

2 + 1

+ 1

I = ∫

= 2∫

= 2arctgt + C = 2arctg

1 + x

+ C .

1 − x2

2 + 1

1 − x

Так как имеет место тождество

= arcsin x + π ,

2arctg

1 + x

(−1 < x < 1) ,

1 − x

то полученный результат в случае b) лишь по форме отличается от резуль- тата в случае а).

Замечание 3. При нахождении интеграла получается результат в раз- ных формах записи, в зависимости от применяемого метода для нахожде- ния интеграла.

с) найдем I = ∫

, применяя

вторую подстановку

Эйлера, т.е.

1 − x2

1 − x2 = xt −1, тогда

1 + 1 − x

I = ∫

= −2∫

= −2arctg t + C = −2arctg

+ C .

1 + t2

1 − x

Заметим, что полученный результат отличается от результатов в слу- чае а) и b) не только по форме записи, но этот результат справедлив для

168

	1 + 1 - x2
промежутков (–1;0) и	(0;1), т.к. при х = 0 выражение -2arctg
промежутков (–1;0) и	(0;1), т.к. при х = 0 выражение -2arctg	x
		x
лишено смысла.
Однако, пределы этого выражения при x→ – 0 и при x→ + 0 различ-

ны: они равны, соответственно, π и – π. Выбирая для промежутков (–1;0) и (0;1) различные значения константы С так, чтобы второе из них было на 2π больше первого. Если принять за значение рассматриваемой функции в точке x = 0 общий предел при x→ – 0 и x→ + 0, то функция будет не- прерывна на (–1;1).

Полученный интеграл с помощью второй подстановки Эйлера – это

тот же результат, как и в случае

а) и b) лишь в другой форме, т.к. имеют

место тождества

arcsin x - p,

0 < x <1

-2arctg

1 +

1 - x2

-1 < x < 0

arcsin x + p,

Пример 4.

Найти интеграл

I = ∫

x +

x2 - x +1

а) применим первую подстановку Эйлера

= t - x; x =

t 2 -1

;

dx =

2(t2 - t +1)dt

x2 - x +1

тогда

2t -1

(2t -1)2

- 2t

dt = ∫

∫

= ∫

dt =

(2t

-1)

+ x2 - x + 1

t(2t -1)

-1

= -

+ 2ln

2t -1

+ C =

2 2t -1

= -

2x + 2 x2 - x + 1

+ 2ln

x +

x2 - x +1

+ C;

2 2x + 2 x2 - x + 1 -1

б) применим вторую подстановку Эйлера для вычисления данного интеграла

x2 - x +1 = tx -1

2t -1

t 2 - t +1

; dx =

-2(t 2 - t +1)

dt ,

x =

;

x2 - x +1

t2 -1

(t 2 -1)2

а x + x2 - x +1 =

, тогда

-1

169

		dx							(-2t2				+ 2t - 2)dt							2			1			3		1			3
∫							= ∫												= ∫		-				-		×			-				dt =
										t(t -1)(t +1)						2												t +			(t +1)		2
	x + x2 - x + 1															2																	2
	x + x2 - x + 1																			t			2(t -1) 2						1
	=			3		+ 2ln		t		-	1	ln		t -1	-		3	ln		t +1		+ C =					3x					+
				3							1						3										3x
				+
			t		1					2						2								x2 - x + 1 + x +1
			t		1					2						2								x2 - x + 1 + x +1

+2ln x2 - x + 1 + 1 - 1 ln x2 - x + 1 - x + 1 - 3 ln x2 - x + 1 + x + 1 + C.
2	2

Отметим, что результаты интегрирования в случаях а) и б) отлича- ются по форме, но в случаях а) и б) подстановки Эйлера приводят к гро- моздким преобразованиям, поэтому если есть возможность, то применяют другие способы нахождения интегралов вида (1), которые рассмотрим ниже.

Отметим, что подынтегральную функцию в (1) представим в виде

			R1	(x)
R(x, ax	2	+ bx + c ) =	R1	(x)	+ R2	(x) ,	(6)

			ax2 + bx + c
			ax2 + bx + c

где R1 и R2 – рациональные дроби.

Представляя R1(x) в виде суммы многочлена Pn(x) и суммы простых дробей, сведем интеграл (1) к линейной комбинации интегралов следую- щих трех видов:

а) ∫	Pn		(x)
				dx ;	(7)

	ax2
		+ bx + c

∫

dx
		;				(8)
		;				(8)
(x - a)m ax2 + bx + c
	dx			2
			k Î N ; p	2	- 4g < 0 .	(9)

(x2 + px + g)k × ax2 + bx + c

Если в (7) Pn (x) = Mx + N ,

то интегралы вида I = ∫

Mx + N

dx с

ax2 + bx + c

помощью подстановки x +

= t

приводятся к виду

I = M1 ∫

tdt

+ N1 ∫

+ K

at 2 + K

где М1, N1, K – некоторые постоянные числа.

170

<<< < Предыдущая 5 6 7 8 9 10 11 12 13 14 15 1617 / 3617 18 19 20 21 22 23 24 25 26 27 28 29 > Следующая >>>

Соседние файлы в папке Высшая математика (РТФ)

#
18.05.20154.76 Mб33умк_Вакульчик_Элементы векторной алгебры.pdf
#
18.05.20155.38 Mб38умк_Вакульчик_Элементы линейной алгебры.pdf
#
18.05.20151.33 Mб40умк_Мальцев_Осн дискретной матем.pdf
#
18.05.20153.75 Mб39умк_Пальчик_Теория вероятностей.pdf
#
18.05.20155.68 Mб32умк_Цывис_Диф.уравнения_Ряды.pdf
#
18.05.20154.7 Mб39умк_Цывис_Функции_Интеграл. исчисл..pdf
#
18.05.20153.54 Mб76умк_Яско_ Диф.уравнения_Ряды.pdf