Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Пензенский Государственный Университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

умк_Цывис_Функции_Интеграл. исчисл

..pdf

Скачиваний:

Добавлен:

18.05.2015

Размер:

4.7 Mб

Скачать

☆

<<< < Предыдущая 2 3 4 5 6 7 8 9 10 11 12 1314 / 3614 15 16 17 18 19 20 21 22 23 24 25 26 > Следующая >>>

Пример 23. Вычислить интеграл

I = ∫

3x2 + 2

dx .

x3 +

2x +10

Решение. I = ∫

3x2 + 2

dx =

d (x3 + 2x +10) = (3x2 + 2)dx

+ 2x +10

= ∫

d (x3 + 2x +10)

= ln

x3 + 2x +10

+ C.

x3 + 2x +10

I = ∫

Пример 24. Вычислить интеграл

sin x

× cos x

∫

dtgx

= ln

tgx

+ C .

Решение. I = ∫

∫

cos2 x

sin x cos x

tgx

или другим способом –

данный интеграл вычислим следующим образом

I = ∫

1× dx

= ∫

(sin2 x + cos2 x)dx

= ∫

sin2 xdx

∫

cos2

xdx

= ∫

sin xdx

sin x cos x

cos x

sin x cos x

+∫

cos xdx

= -∫

d cos x

+ ∫

d sin x

= -ln

cos x

+ ln

sin x

+ C = ln

tgx

+ C.

sin x

cos x

sin x

− 3)

I = ∫

(ln x

Пример 25. Вычислить интеграл

ln x

- 3)

Решение.

I = ∫

(ln x

= ∫

xdx

- 3∫

= ∫

ln x

dx - 3∫

x ln x

− 1

= ∫(ln x)

d ln x - 3∫(ln x)

d ln x =

x - 3 × 2ln

x + C =

x - 6ln

x + C.

Пример 26. Вычислить интеграл

I = ∫

(sin x + cos x)dx

3 sin x - cos x

Решение.

(sin x + cos x)dx

−

I = ∫

= ∫

(sin x - cos x)

3 d (sin x - cos x) =

(sin x - cos x)3 + C .

(sin x - cos x)3

2.3. Метод замены переменной или подстановки

Рассмотрим один из сильнейших методов интегрирования – метод замены переменной или подстановки.

131


Теорема. Пусть функция		x = ϕ(t)			определена и дифференцируема
на [t1,t2 ] , а множество [ x1, x2 ]		–	множество значений этой функции, на
котором определена функция f(x). Если					на [ x1, x2 ] f(x) имеет первооб-
разную, то для любого t [t1,t2 ]		справедлива формула
∫ f (x)dx =	x = j(t)			= ∫ f (j(t)) × j¢(t)dt		(1)

	dx = j¢(t)dt
Формула (1) – формула замены переменной в неопределенном инте-
грале. Суть метода замены переменной в неопределенном интеграле						со-

стоит в следующем: интеграл, стоящий в правой части формулы (1) полу- чаем «проще» или табличного вида, чем интеграл, стоящий в левой части.

Доказательство. Равенство (1) – равенство двух первообразных, по- этому, дифференцируя обе части (1), получим

d (∫ f (x)dx) = f (x)dx = x = j(t) = f (j(t)) × j¢(t)dt d (∫ f (j(t)j¢(t)dt) = f (j(t) × j¢(t))dt

Из последних равенств следует справедливость формулы (1).

Замечание. Если известен интеграл в правой части формулы (1), т.е.

∫ f (j(t))j¢(t)dt = F (t) + C .

Тогда искомый интеграл – как функция от x находим следующим об-

разом: уравнение x = ϕ(t) решают относительно t, т.е. t = j−1(x) , получим

∫ f (x)dx = ∫ f (j(t))j¢(t)dt = F (t) + C = F (j−1(t)) + C .

Замечание. При интегрировании методом замены переменной очень важно удачно найти соответствующую подстановку, т.к. не существует об- щих правил выбора замены переменной для интегрирования любой функ- ции. Умение находить выгодные подстановки можно достичь практикой.

Пример 27. Вычислить интеграл I = ∫ x × 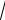x - 3dx .

x - 3 = t

Решение. I = ∫ x x - 3dx = x = t2 + 3 = ∫(t2 + 3) ×t × 2tdt = 2∫(t4 + 6t2 )dt = dx = 2tdt

	t5		6		2	5		3
= 2		+		t3 + C =		(x - 3)	2	+ 3(x - 3)	2	+ C.

5		3		5

132

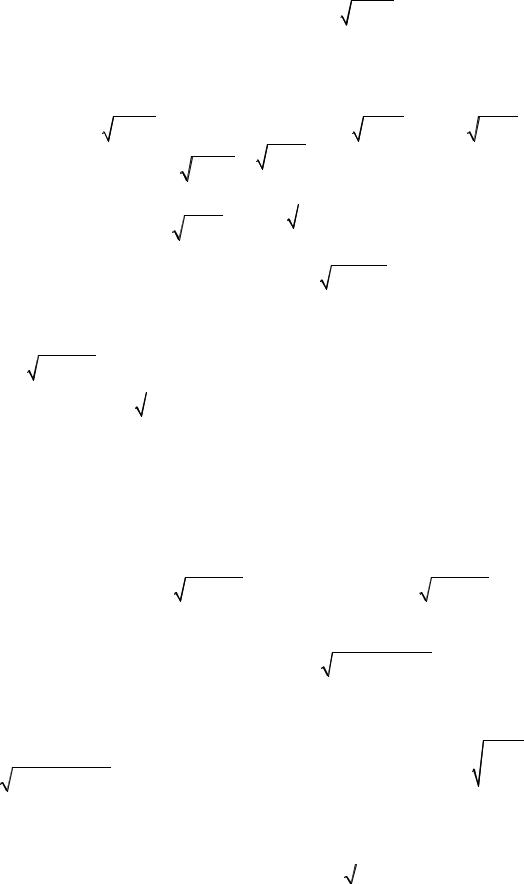
Пример 28. Вычислить интеграл

I = ∫

1 + x2

x =

d (1 + t2 )

Решение.

I =

∫

dx = -

= -∫

tdt

= -

∫

2 1

+ x

1 + t 2

+ t 2

1 + t2

1 + x2 =

= -

+ C = -

1 + x2

1 + t2

+ C.

Пример 29. Вычислить интеграл

I = ∫

a2 - x2 dx .

Решение.

x = a sin t

I = ∫

a2 - x2 dx =

dx = a costdt

= a2 ∫cos2 tdt =

∫(1 + cos 2t)dt =

a2 - x2

= a cost

arcsin

sin 2(arcsin

) =

t +

sin 2t + C =

t = arcsin

arcsin

sin(arcsin

) × cos(arcsin

) =

+ C =

arcsin

- x2

a2 - x2

+ C.

Пример 30. Вычислить интеграл

I = ∫

- a)(b - x)

Решение.

x = a cos2 t + bsin2 t

x - a = (b - a)sin

2 t

I = ∫

= 2∫dj + C =

2arctg

x - a

+ C.

b - x

- a)(b - x)

b - x = (b - a)cos2 t

dx = 2(b - a)sin t costdt

Пример 31. Вычислить интеграл

I = ∫

1 +

1 + x

133

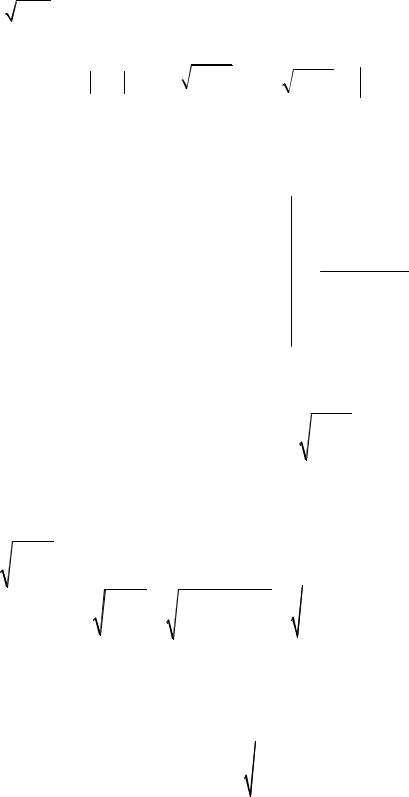
Решение.

x + 1 = t2

2tdt

(t + 1) − 1

I = ∫

x = t

2 − 1

= ∫

= 2∫

dt = 2∫dt − 2∫

t +

+ 1 + x

dx =

2tdt

1 + t

t + 1

= 2t = 2ln t + 1 + c = 2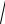t 2 − 1 − 2ln 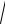t2 − 1 + 1 + C

Пример 32. Вычислить интеграл I = ∫		x2dx	.
	(1	+ x2 )2

Решение.

				x = tgt
I = ∫		x2 dx	=	dx =	dt
I = ∫	(1	+ x2 )2	=	dx =	cos2 t
	(1	+ x2 )2			cos2 t
				1 + x2 = 1 + tg2 x =		1

						cos2 x
						cos2 x

= ∫ tg2t cos4 tdt = ∫sin2 tdt = cos2 t

∫(1 − cos 2t)dt =

−

sin 2t + C =

arctgx −

sin 2arctgt + C.

Пример 33. Вычислить интеграл

I = ∫

a + x

dx .

a − x

Решение.

x = a cos 2t

a + x

I = ∫

dx =

dx = −2a sin 2tdt

= −4a∫cos2 t =

a − x

cos2 t

a + x

a(1 + cos 2t)

cos t

a − x

a(1 − cos 2t)

sin2 t

sin t

= −2a∫(1 + cos 2t)dt = −2at − 2a∫cos 2tdt = −2at − a sin 2t + C =


	x			x 2
= −a arccos		+	1 −		+ C.
= −a arccos		+	1 −		+ C.
	a			a

134

Пример 34. Вычислить интегралы:

34.1. I = ∫

, применяя подстановку

x =

x x2 - 2

Ответ: I =

arccos

+ C .

34.2. I = ∫

применяя подстановку

x = − ln t .

e x + 1

Ответ: I = -ln(1 + e− x ) + C .

34.3. I = ∫

xdx

t =

, применяя подстановку

x +1

x + 1

Ответ: I =

(x +1)3 - 2

+ C .

x + 1

34.4. I = ∫

, применяя подстановку

x =

4 - x2

Ответ. I = -

4 - x

+ C .

34.5. I = ∫

, применяя подстановку

x = sin 2 t .

x(x -1)

Ответ. I = 2arcsin

+ C .

2.4.Метод интегрирования по частям

Кчислу эффективных методов интегрирования относится метод ин- тегрирования по частям. Основывается этот метод на следующей теореме.

Теорема. Если каждая из функций u(x) и	υ(x) дифференцируема
на множестве x и, кроме того, на этом множестве	существует первообраз-
′	x существует первооб-
ная для функции u(x) ×u (x) . Тогда на множестве	x существует первооб-

′
разная и для функции u(x) ×u (x) , причем справедлива формула
∫u(x) × u¢(x)dx = u(x)u(x) - ∫u(x)u¢dx .	(1)
Замечание. Определение дифференциала первого порядка и свойство
инвариантности его формы позволяет записать формулу (1)	в виде
∫ud u = u × u - ∫udu .	(2)

135

Доказательство. Для функций	u(x) и	υ(x) запишем формулу для
производной произведения двух функций
′	′	′	(3)
(u(x) × u(x)) = u(x) × u (x) + u (x) × u(x) .
Интегрируя обе части равенства	(3) и, учитывая, что для всех		x X

существует ∫u(x)u¢(x)dx и ∫(u¢(x)u(x))¢dx = u(x) × u(x) + C , то для всех x

из множества X существует и интеграл ∫u(x)u¢(x)dx , причем справедливы

формулы (1) и (2) – формулы интегрирования по частям.

Суть метода интегрирования по частям состоит в следующем: инте- грал, стоящий в правой части равенства (2) табличный, «проще» или сов- падающий с интегралом, стоящим в левой части равенства (2).

Для применения метода интегрирования по частям, в конкретном случае, требуется уметь разбить заданное подынтегральное выражение на два множителя – на u и на d υ . Общих правил для этого, к сожалению, нельзя дать, кроме:

а) dx всегда должен быть частью d υ ;

в) надо уметь интегрировать d υ (т.е. находить υ);

с) если подынтегральное выражение есть произведение двух функций, тогда наиболее сложный множитель надо рассматривать как часть d υ .

Практика интегрирования показывает, что значительная часть инте- гралов, берущихся посредством интегрирования по частям, может быть разбита на следующие группы:

1. К первой группе относятся интегралы, подынтегральная функция которых содержит в качестве множителя одну из следующих функций: lnx, arcsinx, arctgx, (arctgx)2, ln ϕ(x) . Для вычисления интегралов первой группы

выбирают в качестве u(x)	одну из указанных выше функций.
2. Ко второй группе относятся интегралы вида
∫(ax + b)n cos mxdx,	∫(ax + b)n sin mxdx ,	∫(ax + b)n ekxdx ,
где a, b, k – некоторые постоянные, n – целое положительное число.
Интегралы второй группы берутся путем		n-кратного применения

формулы интегрирования по частям, причем в качестве u(x) всякий раз следует брать (ax + b) в соответствующей степени. После каждого интег- рирования по частям эта степень будет понижаться на единицу.

3. К третьей группе относятся интегралы вида

∫eax sin bxdx , ∫eaxbxdx , ∫sin(ln x)dx .

136

Обозначая любой из интегралов этой группы через I и дважды ин- тегрируя по частям, получим уравнение первого порядка относительно I, решая которое, находим I, а, следовательно, и искомый интеграл.

Замечание. Повторное применение формулы (2) позволяет получить обобщенную формулу интегрирования по частям: если функции u(x) и υ(x) имеют непрерывные производные всех порядков до (n + 1)-го вклю-

′

′ ′′

(n)

, υ

(n)

(n+1)

, то

чительно u ,

υ ,u ,...,u

∫uυ

(n+1)

(n)

′

(n−1)

′′

(n−2)

+ ... +

(−1)

n+1

∫u

(n+1)

υdx .

(4)

dx = uυ

− u υ

+ u υ

Полагая в (4)

n = 1, получим

′′

′

(5)

∫uυ dx = uυ − u υ + ∫u υdx

Пример 35. Вычислить интеграл

I = ∫ x cos xdx .

Решение.

I = ∫ x cos xdx =

u = x;du = dx

= xsin x − ∫sin xdx = x sin x + cos x + C .

d υ = cos x;υ = sin x

Пример 36. Вычислить интеграл

I = ∫ x2 ln xdx .

Решение.

u = ln x; du =

x 3

I = ∫ x2 ln xdx =

ln x − ∫

dx =

ln x −

+ C.

d υ = x2dx;υ =

Пример 37. Вычислить интеграл I = ∫arcsin xdx .

Решение.

u = arcsin x;du =

xdx

I = ∫arcsin xdx =

= x arcsin x − ∫

1 − x2

d υ = dx; υ = x

1 − x2

d (1 − x2 )

= x arcsin x +

∫

= x arcsin x + 1 − x2 + C.

(1 − x2 )2

Пример 38. Вычислить интеграл

I = ∫ xarctgxdx .

137

Решение.

u = arctgx; du =

+ x2

I = ∫ xarctgxdx =

arctgx -

∫

dx =

+ x2

d u = xdx; u =

arctgx -

∫dx +

∫

arctgx -

arctgx + C.

+ x2

Пример 39. Вычислить интеграл

I = ∫

dx .

cos2 x

Решение.

I = ∫

dx =

∫ xdtgx =

u = x; du = dx

= xtgx - ∫tgxdx =

cos2

d u = dtgx;u = tgx

= xtgx - ∫

sin x

dx = xtgx + ∫

d cos x

= xtgx + ln

cos x

+ C.

cos x

Пример 40. Вычислить интеграл

In = ∫cosn xdx .

Решение.

In = ∫cosn xdx = ∫cosn − 2 x(1 - sin2 x)dx = ∫cosn − 2 xdx - ∫cosn − 2 x sin2 xdx =

u = sin x; du = cos xdx

d u = cosn − 2 x sin xdx;u = -∫cosn − 2 xd cos x = -

cosn −1 x

n -1

= In − 2 +

sin x cosn −1 x

∫cosn xdx.

n + 1

n -1

Тогда имеем

In = In−2 +

sin x cosn−1 x

n -1

n -

sin x cosn−1 x

Откуда получим

In 1 -

= In−2 +

n -1

А, следовательно,

sin x cosn−1 x

In = ∫cos

xdx =

n -1

(n ¹ 0)

In−2

Полученная формула сводит вычисление интеграла

к вычисле-

нию интеграла In−2

с меньшим на две единицы индексом.

138

Пример 41. Вычислить интеграл In	= ∫		dx	.
		(x2	+ a2 )n

Решение. Этот интеграл не входит ни в одну из упомянутых выше групп. Для вычисления этого интеграла установим для него рекуррентную фор-

мулу, сводящую вопрос о вычислении

In к вычислению

In−1 . При

n ¹ 1

имеем (n = 1, I1 –

табличный интеграл)

a2dx

((x2 + a2 ) - x2 )

∫

dx =

(x2 + a2 )n

∫

∫ x

xdx

× In −1 -

∫ x

d (x2 + a2 )

+ a

)

n −1

+ a

)

+ a

)

u = x; du = dx

× In −1

d (x2

+ a2 )

d u =

; u =

2a2 (n -1)(x2 + a2 )n −1

(x2 + a2 )n

(n -1)(x2 + a2 )n −1

× In −1

2n - 3

× In −1.

(n -

1)(x

+ a

)

n −1

2n - 2

Таким образом, имеем

In =

2n - 3

In−1 .

-1)(x

+ a

)

n−1

2n - 2

Отметим, что I1

= ∫

arctg

+ C .

+ a2

После того, как вычислен интеграл I1 , полагая в полученной форму-

ле k = 2, находим I2 . В свою очередь зная I2 и полагая в рекуррентной формуле n =3 находим I3 . Продолжая действовать таким образом дальше,

находим интеграл In для любого натурального n.

Пример 42. Вычислить интеграл

I = ∫ 1 + x2 dx .

xdx

u = 1 + x2 ;du =

I = ∫

1 + x2 dx =

Решение.

1 + x2

υ = x; d υ = dx

(1 + x2 ) − 1

= x 1 + x2 − ∫

dx =x 1 + x2 − ∫

dx =

+ x2

1 + x2

= x

1 + x2

− ∫ 1 + x2 dx + ∫

= x 1 + x2

− I + ln(x + 1 + x2 ).

1 + x2

139

или

2I = −x1 + x2 − ln(x + 1 + x2 ) + C .

		1
		1			2			2
Откуда искомый интеграл	I =		x 1 + x			− ln(x +	1 + x		)	+ C .
Откуда искомый интеграл	I =	2	x 1 + x			− ln(x +	1 + x		)	+ C .
		2
Пример 43. Вычислить интеграл				I = ∫eax cosbxdx .

Решение.

u = eax ;du = aeax dx

I = ∫eax cosbxdx = υ = cosbx;υ = 1 sin bx b

= eax sin bx − b

−

∫eax sin bxdx =

u = eax ;du = aeax dx

cos bx

d υ = sin bxdx;υ = −

eax sin bx

eax cosbx −

Таким образом, после двукратного интегрирования I по частям по-

лучили для интеграла I уравнение первого порядка

I =

eax sin bx

eax cos bx −

I .

Решая его относительно I, получим

I =

a cosbx + bsin bx

eax + C .

a2 + b2

Замечание. При вычислении данного интеграла в интегрировании по частям можно дважды было брать тригонометрическую функцию за u.

Замечание. Данный интеграл можно вычислить, используя обобщен- ную формулу интегрирования по частям

′′

′ ′

′′

∫uυ dx = uυ − u υ + ∫u

υdx .

Положим u = cos bx , υ =

eax , тогда u′ = −b sin bx , u′′ = −b2 cos bx , υ′ =

eax

υ′′ = eax . Следовательно искомый интеграл I =

eax

cos bx +

eax sin bx −

I + C ,

откуда I = a cos bx + b sin bx eax + C . a2 + b2

140

<<< < Предыдущая 2 3 4 5 6 7 8 9 10 11 12 1314 / 3614 15 16 17 18 19 20 21 22 23 24 25 26 > Следующая >>>

Соседние файлы в папке Высшая математика (РТФ)

#
18.05.20154.76 Mб33умк_Вакульчик_Элементы векторной алгебры.pdf
#
18.05.20155.38 Mб38умк_Вакульчик_Элементы линейной алгебры.pdf
#
18.05.20151.33 Mб40умк_Мальцев_Осн дискретной матем.pdf
#
18.05.20153.75 Mб39умк_Пальчик_Теория вероятностей.pdf
#
18.05.20155.68 Mб32умк_Цывис_Диф.уравнения_Ряды.pdf
#
18.05.20154.7 Mб39умк_Цывис_Функции_Интеграл. исчисл..pdf
#
18.05.20153.54 Mб76умк_Яско_ Диф.уравнения_Ряды.pdf