умк_Цывис_Функции_Интеграл. исчисл

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Пензенский Государственный Университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Число А называется

пределом функции

z = f (x, y) при x → x0 ,

y → y0 , т.е. в точке M 0 (x0 , y0 ) , если для любого

ε > 0 существует δ > 0 ,

что для любой точки M(x, y)

0 < (x − x )2 + ( y − y )2 < δ2

f (x, y) − A

0 < (x − x )2 + ( y − y )2 < δ2

f (x, y) − A

..pdf

Скачиваний:

Добавлен:

18.05.2015

Размер:

4.7 Mб

Скачать

☆

<<< < Предыдущая 1 23 / 363 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

Рассмотрим примеры и задачи на определение функции нескольких переменных и нахождение области определения.

Найти область определения функций:

а) z = xy2 − 4 y − x + 1;

в) z = 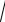(x −1)( y − 2) ;

д) z = ln xy ;

б)

г)

е)

z = 2x − y ; x − y

z = ln x + ln y ;

z =		x + y + z
			.

	1 − x2 − y2 − z2

Решение:

а) в данном случае выражение, стоящее в правой части имеет смысл при любых x и y, следовательно, область определения данной функции вся плоскость, т.е. R2 ;

б) выражение, стоящее в правой части, не имеет смысла (на 0 делить нельзя), когда y = x. Значит областью определения является вся плос- кость, за исключением прямой y = x (рис. 6);

в) квадратный корень принимает действительные значения, если подкоренное выражение принимает неотрицательные значения, т.е. об- ласть определения данной функции совпадает с множеством решения не- равенства (x -1)( y - 2) ³ 0 (рис. 7);

y	y
y
	y = x
	1
	x	2	x
	0	2	x
Рис. 6		Рис. 7
Рис. 6

г) так как выражение, стоящее под знаком логарифма должно быть положительным, то область определения данной функции совпадает с

	x > 0	– а это первая четверть
множеством решения системы неравенств	y > 0	– а это первая четверть

для плоскости xOy;

д) так как выражение, стоящее под знаком логарифма должно быть

выражение положительное, то область определения данной функции сов-

падает с множеством решения неравенства xy > 0 , из которого следует:

либо x > 0 и y > 0 ; либо x < 0 и y < 0 . Таким образом имеем область,

состоящую из первой и третьей четвертей координатной плоскости;

е) нахождение области определения функции трех переменных вы-

полняется точно так же, как и в случае функций двух переменных. В дан-

ном примере область определения функции совпадает с множеством реше-

ния неравенства

1 − x2 − y2 − z2 > 0 , т.е. x2 + y2 + z2 < 1. А это открытый

шар с центром в начале координат радиуса 1.

§ 5. Предел функции нескольких переменных

Пусть

на

плоскости R2

задана

последовательность

точек

{M k (xk , yk )}.

Говорят,

что эта последовательность сходится к точке

(x , y

) R2 ,

если

расстояние

ρ(M

, M

) =

− x )2

+ ( y

− y )2

стремится к нулю при k → ∞ , т.е.

lim ρ(M

, M

) = lim

− x )2

+ ( y

− y )2

= 0 .

k →∞

Множество внутренних точек круга с центром в точке

P0 и радиу-

сом R называют окрестность точки P0 .

Таким образом, последовательность точек

M k R2 , k =

сходит-

1, ∞

ся к точке M 0 , если в любой окрестности точки

M 0 находятся все точки

последовательности M k

«быть может» за исключением конечного числа,

т.е., начиная с некоторого номера N.

Точка M 0 D R2

– предельная точка множества D, значит существует

последовательность точек

M k Î D , сходящихся к M 0 ,

т.е.

M 0 = lim M k , или

k →∞

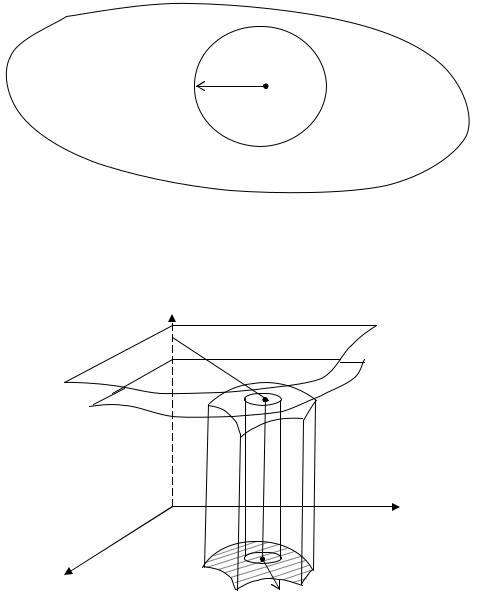
ε > 0 существует nε > 0 , такое, что m N и m ³ nε r(M 0 , M k ) £ e (рис. 1).

εM 0

Рис. 1

Определение предела функции двух переменных по Коши (рис. 2).

А + ε

А	z = A + ε
А – ε	z = A – ε

M 0 (x0 , y0 )

Рис. 2

Определение предела функции двух переменных по Гейне.

Число А называется пределом функции z = f (x, y) в точке P0 (x0 , y0 ) ,

если для любой сходящейся к M 0 (x0 , y0 ) последовательности точек

M 0 (x0 , y0 )

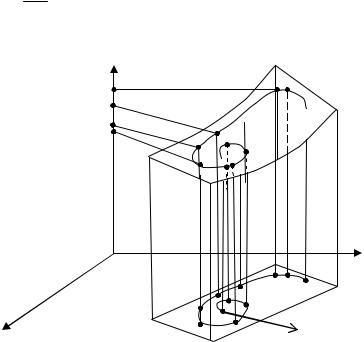
M k (xk , yk ), k = 1, ∞ , соответствующая последовательность f (M k ) значе-

ний функции сходится к А (рис. 3).

Г f

M k (xk , yk )

M 0 (x0 , y0 )

Рис. 3

Доказывается, что приведенные два определения предела функции двух переменных эквивалентные, но при доказательстве того, что данное число А не является пределом функции, удобно пользоваться определени- ем предела по Гейне (т.е. через последовательности).

При определении предела функции z = f (x, y) в точке

полагают, что функция может быть не определена в точке M 0 . Из этого

следует, что значения функции f(M)	отличаются от числа А на достаточно
малую величину, если точка М выбрана достаточно близко к точке		M 0 .
Из определения предела функции по Коши получаем неравенство вида
A − ε < f (x, y) < A + ε ,		(1)
для любой точки M(x, y), такой, что
0 < (x − x )2	+ ( y − y )2 < δ2 .	(2)
0	0

С геометрической точки зрения неравенство (1) означает следующее: любая точка M(x, y), удовлетворяющая условию (2) (лежит в окрестности точки M0 ) находится между двумя плоскостями z = A − ε и z = A + ε , или,

другими словами, предел функции z = f (x, y) при M (x, y) → M 0 (x0 , y0 ) определяется поведением функции в окрестности точки M0 (x0 , y0 ) и не зависит от значения функции в этой точке.

Отметим, что размеры δ-окрестности точки M0 (x0 , y0 ) существенно

зависит от величины ε.
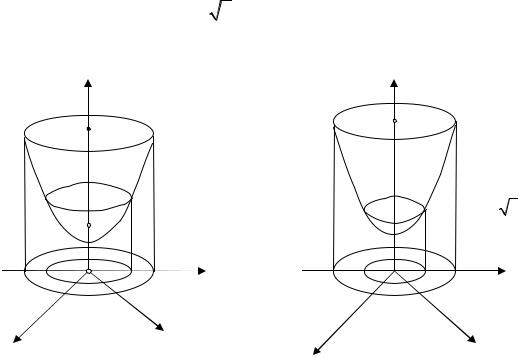
Так, например,	lim		(x2 + y2 −1) = 1, если выбираем ε = 1, то
	( x, y)	→(0,0)

δ ≤ 1 (рис. 4), а при ε = 0,5			δ ≤		2	(рис. 5).
δ ≤ 1 (рис. 4), а при ε = 0,5			δ ≤			(рис. 5).
				2
z						z

A = 1

ε =

δε ≤ 1

δε

≤

δε

(0,0)

Рис. 4

Рис. 5

А если ищем предел

f (x, y) = x2 + y2 + 1 в точке

;

, то преде-

лом является число А = 1,5 и при

ε < 0,5 , δ-окрестность точки

;

–

это круг с центром

этой

точке,

расположенный

кольце

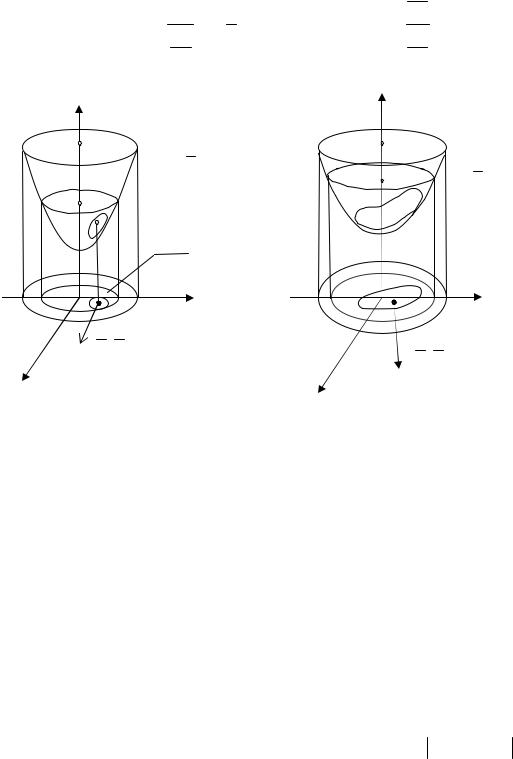
1,5 − ε < x2 + y2 + 1 < 1,5 + ε (рис. 6). Если выбрать ε > 0,5 , то размеры

должны быть такие, чтобы

δ-окрестность

располагалась

внутри круга

x2 + y2 < R2 , где R > 1 (рис. 7).

Пример. Доказать, что функция f (x, y) =

x2 − y2

не имеет предела

x2 + y2

в точке О(0, 0).

Решение:

1 способ. Выберем две сходящиеся к точке

О(0, 0) последовательно-

сти точек, например, M1 =

M 2 =

, тогда

		− 3				1
lim f (M1) = lim		n2	= − 3 ;	lim	f (M 2 ) = lim	n2	= 1.
n→∞	n→∞	5	5	n→∞	n→∞	1
		n2				n2
z					z
	ε = 1						ε = 1
		2					ε = 1
A	A = 1,5						2
							x2 + y2 < R2
	0 < x2 + y2 < 1						R > 1
							R > 1
			y				y
			y
( 1 ; 1 )						1	1
2	2					( ;	)
x						2	2
x					x
					x
Рис. 6					Рис. 7

Таким образом, двум различным последовательностям точек, сходя- щимся к точке О(0, 0) (т.е. имеющим один и тот же предел), соответствует две последовательности значений функции, имеющие разные пределы. То- гда согласно определению предела функции по Гейне, данная функция не

имеет предела в точке О(0, 0).				x = r cos ϕ, y = r sin ϕ .
2 способ. Перейдем к полярным координатам				x = r cos ϕ, y = r sin ϕ .
Тогда f(x, y) примет вид
f (x, y) = f (r cos ϕ, r sin ϕ) =	r2 cos2		ϕ − r3 sin	2 ϕ	= cos 2ϕ .
f (x, y) = f (r cos ϕ, r sin ϕ) =	r	2 cos2	ϕ + r 2 sin	2 ϕ	= cos 2ϕ .
	r	2 cos2	ϕ + r 2 sin	2 ϕ
Если бы существовал предел lim f (x, y) = A ,				то для любого ε > 0
	x	→0
	y	→0

нашлось бы δ > 0 , что из неравенства 0 < r < δ следует, что f (x, y) − A < ε .

Но функция cos 2ϕ не зависит от r, и в любой сколь угодно малой окре- стности точки О(0, 0) есть как точки, где f (r cos ϕ, r sin ϕ) = 0 (например,

при ϕ = π ), так и точки, где f (r cos ϕ, r sin ϕ) = 1 (например, при ϕ = 0 ). 4

Значит искомый предел не существует.

Приведенные выше определения предела функций двух переменных аналогично обобщаются на случай функции трех и большего числа пере- менных. Используя понятие предела, вводится понятие бесконечно малой функции, изучаются свойства бесконечно малых функций, теоремы об арифметических операциях над пределами и другие свойства, аналогичные случаю одной переменной.

Наряду с указанными выше пределами у функций многих перемен- ных можно рассматривать и пределы других видов, связанные с последо- вательным переходом к пределу, например по различным координатам, т.е. пределы вида (для случая двух переменных)

lim lim f (x, y) или	lim lim f (x, y) ,
x→ x0 y → y0	y → y0 x→ x0

где функция f(x, y) определена в некоторой окрестности точки (x0 , y0 )

кроме, «быть может», в самой точке.

Пределы указанного вида называются повторными пределами, они представляют собой специфику функций нескольких переменных. Таким образом, повторные пределы соответствуют предельному переходу (для двух переменных x и y) сначала по x при постоянном значении y ( y ¹ y0 ) ,

а затем по y при постоянном значении			x (x ¹ x0 ) или наоборот.
Пусть функция z = f (x, y) определена в окрестности точки (x0 , y0 ) ,
кроме «может быть» прямых x = x0 и			y = y0 . При фиксированном значе-
нии переменной y функция	z = f (x, y)			– функция одной переменной x.
Пусть для любого фиксированного значения y					из окрестности точки y0 ,
существует предел функции	f(x,y)	при		x ® x0	(это предел зависит «во-
обще говоря» и от y):
	lim	f (x, y) = j( y)
x→ x0
y −фиксир.

Пусть предел функции ϕ( y) , при y ® y0 , существует и равен А:

lim ϕ( y) = A .

y→ y0

Тогда говорят, что в точке M 0 (x0 , y0 ) существует повторный пре-

дел функции f(x, y) и записывают следующим образом

lim lim f (x, y) = A .

y → y0 x→ x0

При этом lim f (x, y) = ϕ( y) , y – фиксированное значение						называ-
x→ x0
ется внутренним пределом в повторном пределе.
Аналогичным образом определяется другой повторный						предел
lim lim f (x, y) , в котором внутренним пределом является					lim	f (x, y) ,
x→ x0 y → y0					y → y0
x – фиксированное значение.
	f (x, y) =	xy
Например, для функции			,	область определения ко-
Например, для функции		x 2 + y 2	,	область определения ко-

торой является вся плоскость за исключением начала координат, оба по- вторных предела существуют и

lim lim f (x, y) = lim lim f (x, y) = 0 .
x→0 y→0	y→0 x→0

Предел lim f (x, y)		не существует, т.к. например, вдоль координат-
( x, y)→(0,0)
ных осей он равен нулю, а вдоль прямой y = x предел равен 0,5.
А для функции
				0, при x = 0 или y = 0
f (x, y) =			1		1
	xsin		1	+ y sin	1	, если x ¹ 0 и y ¹ 0,
	xsin			+ y sin		, если x ¹ 0 и y ¹ 0,
			y		x
			y		x

имеющую областью определения всю плоскость, найдем различные ее пре- делы. Так lim f (x, y) = 0 , а что касается повторных пределов для данной

( x, y)→(0,0)

функции, то они

lim (lim x sin

+ lim y sin

) и lim( lim x sin

+ lim y sin

)

y→0 x→0

y x→0

x→0 y→0

y y

→0

не

существуют, так

как уже

не существуют

lim y × sin

( y ¹ 0) и

x→0

lim x × sin

(x ¹ 0) .

y→0

Для функции

f (x, y) =

при (x, y) → (0,0)

существует пре-

1 + x2 y 2

дел, равный нулю, существуют и равны нулю оба повторных предела:

lim

= lim 0

= 0 ,

lim

= lim 0

= 0 .

lim

+ x

lim

+ x

x→0 y→0 1

x→0

y→0 x→0 1

y→0

Таким образом, только из существования предела функции в данной точке не следует существования повторных пределов в этой точке, и, на- оборот, из существования повторных пределов не следует существования предела в соответствующей точке. Тем не менее, определенную связь ме- жду этими пределами (понятиями) устанавливает следующая теорема.

Теорема 3. Если в точке

M 0 (x0 , y0 ) существует предел функции

f(x, y), равный

А (lim f (x, y) = A ), а также пределы в повторных пределах

( x, y)→(0,0)

этой функции, тогда существуют повторные пределы

lim lim f (x, y)

x→x0

y→ y0

lim

lim f (x, y) , причем имеет место равенство

y→ y0 x→x0

lim

lim f (x, y) = lim lim f (x, y) = A .

x→x0 y→ y0

y→ y0 x

→x0

Доказательство. Проведем доказательство теоремы для случая, ко-

гда существует lim f (x, y) = A и при любом y (“ быть может”

за исключе-

( x, y)→( x0 , y0 )

нием

y0 )

из

окрестности

точки

(x0 , y0 ) существует

предел

lim

f (x, y) = ϕ( y) , тогда повторный предел lim lim f (x, y)

существует

x→ x0

y→ y0 x→x0

и имеет место равенство lim lim

f (x, y) = A .

y→ y0 x→x0

Действительно, так как существует

lim f (x, y) = A , то для любого

( x, y)→( x0 , y0 )

ε > 0

существует

δε –

окрестность точки

M0 (x0 , y0 ) , такая, что имеет ме-

сто неравенство

f (x, y) − A

Так как существует lim f (x, y) = ϕ( y) , то для любого числа

из

x→ x0

окрестности точки M0 (x0 , y0 ) и из последнего неравенства будем иметь

ϕ( y) − A

≤

< ε ,

что означает, что

lim

ϕ( y) = lim

lim f (x, y) = A . Теорема доказана.

y→ y0

y→ y0 x→ x0

Отметим, что обратное утверждение неверно.

Замечание. Понятие повторных пределов функции можно ввести и для

случая, когда

x0 (либо y0 , либо x0 и y0 ) равна + ∞ (или

− ∞ , или + ∞ ).

§6. Непрерывность функции нескольких переменных

Пусть в пространстве					R 2 задана область D и точка M 0 (x0 , y0 ) ,
принадлежащая D. Функция					z = f (x, y) называется непрерывной в точке
M 0 (x0 , y0 ) , если выполняются следующие условия:
1.	f(M)	определяется в точке M 0 и некоторой ее окрестности;
2.	существует			lim f (M ) ;
			M →M 0
3.	lim	f (M ) = f (M 0 ) .
	M → M 0
Если в точке			M 0	одно из условий, приведенных выше, не выполня-
ется, то точка		M 0 –	точка разрыва функции z = f (x, y) .

Аналогично определяется непрерывность в точке для функций 3 и большего числа независимых переменных.

Для функции z = f (x, y) двух независимых переменных точки раз-

рыва могут быть изолированными или образовывать линию разрыва, а для функции w = f (x, y, z) трех независимых переменных точки разрыва мо-

гут быть изолированными, образовывать линию или поверхность разрыва.

Пример 1. Найти точки разрыва функций:

а) z =

;

б) z =

;

x 2 + y 2

(x - 4) 2 + ( y - 2)2

в) z =

2x + y

;

г) w =

x + y

x2 − y 2

x 2

+ y 2 + z 2 - 4

Решение:

а) данная функция определена на

R 2 всюду, кроме точки

О(0,0), ко-

торая и является точкой разрыва функции;

б) точка разрыва функции – А(4; 2);

в)

данная

функция

определена для

любых

y, таких,

что

x 2 - y 2 ¹ 0 . Следовательно,

прямые

x = y

и x = − y являются линиями

разрыва данной функции;

г)

данная

функция определена

для любых x,

и z,

таких,

что

x 2 + y 2 + z 2 ¹ 4 . Сфера с центром в начале координат, радиусом 2 являет-

ся поверхностью разрыва функции.

Функция z = f (M ) называется непрерывной на множестве D, если она непрерывна в каждой точке этого множества.

<<< < Предыдущая 1 23 / 363 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

Соседние файлы в папке Высшая математика (РТФ)

#
18.05.20154.76 Mб33умк_Вакульчик_Элементы векторной алгебры.pdf
#
18.05.20155.38 Mб38умк_Вакульчик_Элементы линейной алгебры.pdf
#
18.05.20151.33 Mб40умк_Мальцев_Осн дискретной матем.pdf
#
18.05.20153.75 Mб39умк_Пальчик_Теория вероятностей.pdf
#
18.05.20155.68 Mб32умк_Цывис_Диф.уравнения_Ряды.pdf
#
18.05.20154.7 Mб39умк_Цывис_Функции_Интеграл. исчисл..pdf
#
18.05.20153.54 Mб76умк_Яско_ Диф.уравнения_Ряды.pdf