
14-es / Высшая математика (РТФ) / умк_Цывис_Функции_Интеграл. исчисл
..pdf
сти ( Ax + By + Cz + D = 0) xOy |
– это |
уравнение |
вида z = 0 , то |
есть |
|||||
A = B = D = 0 и C = 1. Из условия параллельности прямой l |
|
||||||||
|
x − x0 |
= |
y − y0 |
= |
z − z0 |
(l) |
|
|
|
|
|
|
|
|
|
||||
|
m |
n |
p |
|
|
||||
и плоскости Ax + By + Cz + D = 0 . |
|
|
|
|
|
|
|||
Имеем Am + Bn + Cp = 0 , откуда |
p = 0 , т.е. |
(x + z) - ( y - z) = 0 |
или |
||||||
x + z = y − z . |
|
|
|
|
|
|
|||
По уравнению поверхности (а это цилиндр) заключаем, что искомое геометрическое место точек определяется уравнениями:
x + z = y - z = 3 или x + z = y - z = 3
Пример 4. Написать уравнения касательной прямой и нормальной плоскости к линии, заданной в параметрической форме:
x = |
|
|
|
|
|
2 cost |
|
||
|
|
|
|
π |
|
|
|
||
|
|
2 sin t в точке M0 , если t0 = |
||
y = |
|
. |
||
|
|
|
|
4 |
z = |
4t |
|
||
|
|
|
|
|
Решение. Определим координаты точки |
M 0 (x0 , y0 , z0 ) : |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
x0 = 1; y0 = 1; z0 = π . |
||||||
Находим производные функций x(t), y(t), z(t) и их значения в точ- |
||||||||||||||||
ке M0 (1,1, π) , получим |
|
|
|
|
|
|
|
|
|
|||||||
4 |
|
|
xt′ = − |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
xt′(t0 ) = −1; |
|||
|
|
|
|
|
2 sin t; |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
yt′ |
= |
2 cost; |
|
|
|
yt′(t0 ) =1; |
|||||
|
|
|
|
|
zt′ |
= 4 |
|
|
|
|
|
|
|
|
zt′(t0 ) = 4 |
|
Тогда уравнения касательной прямой и уравнение нормальной плос- |
||||||||||||||||
кости соответственно имеют вид: |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
x −1 |
= |
y −1 |
= |
z − π |
|
|
|
|
|
|
|
|
|
|
|
|
−1 |
|
1 |
|
1 |
|
|
-1(x -1) + ( y -1) ×1 +1× (z - p) = 0 |
или |
x - y - 4z + 4p = 0 . |
|||||||||||||
Пример 5. Написать уравнения касательных плоскостей и нормалей |
||||||||||||||||
к заданным поверхностям в указанных точках: |
|
|||||||||||||||
1) z = x × y |
|
в точке M (1,1, -1) ; |
|
|
||||||||||||
2) |
x2 |
+ |
y2 |
− |
z2 |
|
= 1 |
|
|
в точке |
M (5, -4,3) ; |
|||||
|
|
|
|
|
|
|||||||||||
25 |
16 |
9 |
|
|
|
|
|
|
|
|
|
|
|
|||
111
3) |
x2 |
− |
y2 |
− |
z2 |
= 1 в точке M (x , y , z |
|
) ; |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
a2 |
|
b2 |
|
c2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
4) |
x3 + y3 + z3 + xyz = 6 |
|
|
в точке |
M (1, 2, −1) ; |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
5) |
xy2 + z3 = 12 |
в точке M (1,2,2) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
Ответы: 1) x + y − z −1 = 0; |
|
|
x −1 |
= |
|
y −1 |
= |
|
z −1 |
; |
|
|
|
|
|
|
||||||||||||||||||||||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
−1 |
|
|
|
|
|
|
|
|
|
|
||||||||||
2) 12x −15 y − 20z − 60 = 0; |
x − 5 |
= |
y + 4 |
= |
z − 3 |
; |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
−15 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |
|
|
|
|
|
|
|
|
−20 |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
a2 |
|
|
|
|
|
b2 |
|
|
|
|
c2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
xx |
|
yy |
|
zz |
0 |
|
||||||||||||||
3) |
|
(x − x ) − |
|
|
|
( y − y ) − |
|
|
|
|
(z − z ) = |
0; |
|
|
|
|
0 |
|
− |
0 |
− |
|
= 1; |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
x0 |
|
|
0 |
|
|
y0 |
0 |
|
|
z0 |
|
|
0 |
|
|
|
|
|
|
|
|
|
a2 |
|
b2 |
|
c2 |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
4) x + 11y + 5z −18 = 0; |
|
x −1 |
= |
y − 2 |
= |
z + 1 |
; |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
11 |
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
5) x + y + 3z = 9; |
|
x −1 |
= |
y − 2 |
= |
z − 2 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Пример 6. Написать уравнения касательной прямой и нормальной плоскости к линии в точке:
1)x = t; y = t 2 ; z = t2 ; t = −1;
2)x = z; y = x = z2 в точке M (−1,1, −1) .
Ответы:
1) |
x + 1 |
= |
y −1 |
= |
|
x + 1 |
; x − 2 y + 3z + 6 = 0 ; |
|
1 |
−2 |
|
|
|
||||
|
|
3 |
|
|
||||
2) |
x + 1 |
= |
y −1 |
= |
z + 1 |
; x − 2 y + z + 4 = 0 . |
||
1 |
−2 |
|
||||||
|
|
1 |
|
|
||||
Пример 7. На линии x = t3, y = t 2 − 2t; z = t 2 + 2t найдите точки, в
которых касательная прямая параллельна плоскости 2x − 3y − 3z + 5 = 0 .
Ответ: O(0,0,0), M (8,0,8) .
Экстремумы. Наибольшее и наименьшее значения функции
Пример 8. Исследовать на экстремумы функцию
z = ( y − x)2 + ( y + 2)3 .
112
Решение. Определим критические точки данной функции
¶z = -2( y - x) = 0
¶x
¶z = 2( y - x) + 3( y + 2)2
¶y
Решая |
полученную систему, |
находим |
x = −2; y = −2 , т.е. точку |
||||
M0 (−2, −2) . Проверим достаточные условия экстремума в этой точке |
|||||||
¶2 z = 2; A = 2; |
|
¶2 z |
= -2; B = -2; |
¶2 z = 2 + 6( y + 2); C = 2; AC - B2 = 0 |
|||
|
|
||||||
¶x2 |
|
¶x¶y |
¶y2 |
|
|
||
Так как AC - B2 = 0 , то в этом случае для решения вопроса об экс- |
|||||||
тремуме функции |
z нужны дополнительные исследования. Учитывая, что |
||||||
z(−2, −2) = 0 , то достаточно исследовать знак функции |
z в окрестности |
||||||
точки M0 (−2, −2) . |
|
|
|
||||
Исследуем знак функции z вдоль прямой |
y = x (первое слагаемое в |
||||||
функции z |
в этом случае равно 0). |
Знак функции z определяется знаком |
|||||
слагаемого |
( y + 2)3 . Так, если y < −2 , то ( y + 2)3 < 0 ; |
если y > −2 , то |
|||||
( y + 2)3 > 0 . Таким образом, в любой окрестности точки |
M0 (−2, −2) есть |
||||||
как положительные, так и отрицательные значения функции, т.е. функция сохраняет определенный знак. В точке M0 (−2, −2) функция экстремума не имеет.
Пример 9. Исследовать на экстремум
1)z = x3 y2 × (6 - x - y) ;
2)z = x3 + y3 - 3axy ;
3)z = x × e y + x sin y ;
4)z = x2 - 2xy + y4 - y5 ;
5)z = 2 + (x - y)2 + ( y -1)4 .
Ответы:
1)максимум (3; 2);
2)минимум (а, а) при a > 0 , максимум (а, а) при a < 0 ;
3)экстремума нет;
4)в точке (0,0) нужны дополнительные исследования. Экстремума нет;
5)в точке (1, 1) нужны дополнительные исследования. Минимум.
113
y
A
x = 0 |
x + y = 1 |
D
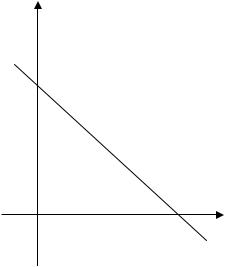
Пример 10. Найти наибольшее и наименьшее значения функции
f (x, y) = x2 + y2 + x |
в области D: |
x + y £1, x ³ 0, y ³ 0 . |
|
Решение.
1. На плоскости xOy построим об- ласть D
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2. |
|
|
Найдем |
критические |
|
точки |
||||||||||||||||
|
0 |
|
|
|
y = 0 |
B |
x |
функции f (x, y) |
в области D. |
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
∂f |
= 2x + 1 = 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂x |
= 2 y = 0 |
|
|
x = − 2 |
M |
0 |
− |
|
|
|
,0 . |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂f |
|
|
|
y = 0 |
|
|
|
2 |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
∂y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Точка M 0 − |
|
|
;0 |
не принадлежит области D. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
3. |
Исследуем |
на |
наибольшее |
|
|
и |
наименьшее |
|
значение |
функцию |
||||||||||||||||||||||||||||||
f (x, y) |
на границе области D. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
3.1. OB : y = 0; |
x [0;1] f (x,0) = x2 + x; |
|
|
df |
= 2x + 1; |
2x + 1 = 0 x = − |
1 |
. |
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
2 |
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Следовательно, |
f (x,0) |
не |
имеет |
|
|
|
критических |
точек |
на |
ОВ, |
т.к. |
||||||||||||||||||||||||||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
[0,1]. |
Найдем значение |
f (x,0) |
на концах отрезка [0,1], получим |
|
||||||||||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (0,0) = 0, |
f (1,0) = 2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
3.2. AB : y + x = 1; |
x [0,1]; f (x, 1 − x) = x2 + (1 − x)2 + x; |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
df |
|
= 2x − 2(1 − x) + 1 = 4x −1; 4x −1 = 0; |
x = |
1 |
. |
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
3 |
|
1 |
3 |
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Единственная критическая точка |
|
|
|
|
, |
|
|
; f |
|
, |
|
= |
|
. Найдем значение |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
8 |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
4 |
|
4 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
f (x, x − 1) на концах отрезка [0,1], получим |
f (0, 0) = 0; f (0,1) = 1. |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
3.3. AO : x = 0; |
y [0,1]; f (0, y) = y 2 ; |
df |
|
= 2 y = 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Критическая точка (0,0): |
f (0,0) = 0 , а |
|
|
|
f (0,1) = 1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
4. Сравнивая значения функции в полученных точках, имеем |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
max |
f (x, y) = f (1,0) = 2; |
min |
f (x, y) = f (0,0) = 0 . |
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
D |
|
|
|
|
|
|
|
|
|
|
D |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
114
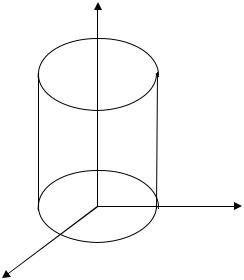
Пример 11. Найти наибольшее и наименьшее значения координат точек цилиндра высотой 1 с образующей ок- ружностью радиуса 2 с центром в на- чале координат.
Решение. 1) Данную задачу можно записать следующим образом: найти наибольшее и наименьшее зна-
чения функции f (x, y, z) = x × y × z в об- |
||
ласти D R2 ; x2 + y 2 ≤ 4; 0 ≤ z ≤ 1. |
||
2) |
Найдем |
критические точки |
функции |
f (x, y, z) |
в области D0 . Об- |
ласть D в R3 имеет вид
А область D0 : x2 + y2 < 4; 0 < z < 1
∂f |
|
= yz |
|
|
∂x |
||
|
∂f |
|
|
|
|
= xz |
|
|
∂y |
|
|
|
|
|
|
|
∂z |
= yx |
|
|
∂z |
||
|
|
|
|
z
S3
S2
S1
0 |
y |
x
M (x,0,0)
N (0, y,0)
P(0,0, z)
Точки M, N, P – |
являются решением полученной системы. Но из то- |
||||||||||
чек M, N и P области |
D0 принадлежат только точки P(0,0,z) при 0 < z < 1. |
||||||||||
Таким образом, имеем линию критических точек и |
f (P) = 0 . |
|
|
||||||||
3) |
Рассмотрим |
функцию |
f (x, y, z) |
на |
поверхности |
||||||
S1 = {(x, y, z) R3 |
|
|
|
x2 + y2 < 4; |
z = 0}. На поверхности |
S1 f (x, y, z) |
принима- |
||||
|
|||||||||||
ет постоянное значение: f (S1) = 0 (т.е. |
все точки поверхности |
S1 – кри- |
|||||||||
тические точки f (x, y, z) ). |
|
|
|
|
|
||||||
4) |
Рассмотрим |
функцию |
f (x, y, z) |
на |
поверхности |
||||||
S2 = {(x, y, z) R3 |
|
x2 + y2 = 4; 0 < z < 1}. Критические точки |
f (x, y, z) на |
||||||||
|
|||||||||||
поверхности S2 – это критические точки функции |
f (x, y, z) |
при условии |
|||||||||
x2 + y2 = 4 |
(0 < z < 1) . Для этого находим функцию Лагранжа, |
которую |
|||||||||
запишем в виде
Φ(a, y, z,λ) = f (x, y, z) − λ(x2 + y2 − 4) = xyz − λ(x2 + y2 − 4) .
115
Критические точки Φ(x, y, z,λ) найдем, решая систему уравнений
¶F
¶x = yz - 2lx = 0¶F = xz - 2ly = 0
¶y
¶F = xy = 0
¶z
¶F = x2 + y2 - 4 = 0¶l
Из третьего уравнения системы имеем либо |
x = 0 , либо y = 0 ; если |
||
x = 0 , то из первого уравнения либо |
y = 0 , либо |
z = 0 ; но это невозможно |
|
из-за уравнения четвертого, т.к. при |
x = 0 и y = 0 x2 + y2 - 4 ¹ 0 ; если |
||
же x = 0 и |
z = 0 , то тоже невозможно, т.к. 0 < z < 1. |
||
Если |
y = 0 , то из второго уравнения имеем либо x = 0 , либо z = 0 ; |
||
если y = 0 |
и x = 0 , то это невозможно из-за четвертого уравнения; если |
||
y = 0 и |
z = 0 , то это невозможно из-за условия 0 < z < 1. |
|
|
|||||||
Следовательно, функция Φ(x, y, z,λ) критических точек не имеет, а |
||||||||||
значит нет критических точек функции |
f (x, y, z) на |
S2 . |
|
|
||||||
5) |
Рассмотрим |
функцию |
f (x, y, z) |
на |
поверхности |
|||||
S3 = {(x, y, z) Î R3 |
|
z =1, x2 + y2 < 4} . Уравнение поверхности |
S3 |
z = 1, то- |
||||||
|
||||||||||
гда f (x, y, z) = xy . Находим критические точки функции |
f (x, y,1) = xy в |
|||||||||
области |
x2 + y2 < 4 : |
|
|
|
|
|
|
|
||
|
|
|
|
|
¶f |
= y = 0 |
|
|
|
|
|
|
|
|
|
¶x |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¶f |
|
|
|
|
|
|
|
|
|
|
¶y = x = 0. |
|
|
|
||
|
|
|
|
|
|
|
|
|||
Единственная критическая точка |
f (x, y, z) на S3 – это точка |
(0, 0, 1) |
||||||||
и f (0, |
0, 1) = 0 . |
|
|
|
|
|
|
|
|
|
6) Рассмотрим функцию |
f (x, y, z) на линии |
l12 = S1 Ç S2 . В этом |
||||||||
случае |
f (x, y, z) = f (L12 ) = 0 , т.е. все точки этой линии критические. |
|||||||||
7) Для линии L23 = S2 Ç S3 |
задача состоит в исследовании функции Ла- |
|||||||||
гранжа, которая имеет вид
F(x, y,l) = f (x, y,1) - l(x2 + y2 - 4) .
116

Критические точки данной функции найдем из системы уравнений
|
|
y − 2λx = 0 |
|
|
|
|
|
||||
|
|
|
|
− 2λy = 0 |
|
|
|
|
|
||
|
|
x |
|
|
|
|
|
|
|||
|
|
|
2 |
+ y2 − 4 = 0 |
|
|
|||||
|
|
x |
|
|
|||||||
Если вычесть из первого уравнений второе уравнение, то получим |
|||||||||||
( y − x) + 2λ( y − x) = 0 или |
(1 + 2λ)( y − x) = 0 |
||||||||||
|
|
|
|
|
|
|
получим x2,3 = y2,3 = ± |
|
|||
Откуда, используя третье уравнение системы, |
2 |
||||||||||
(z = 1) , или λ = − |
1 |
, тогда x = − y |
и из третьего уравнения получим |
||||||||
|
|||||||||||
2 |
x4,5 = ± |
|
|
|
y4,5 = ± |
|
|
|
z = 1. |
||
|
|
|
|
|
|
|
|||||
|
|
2; |
2; |
||||||||
Для полученных точек имеем
f (x2 , y2 ,1) = f (x3 , y3,1) = 2 − max
f(x4 , y4 ,1) = f (x5 , y5 ,1) = −2 − min .
8)Сравнивая значения функции f (x, y, z) в полученных точках, по-
лучим, что max f (x, y, z) = 2 , а min f (x, y, z) = −2 .
Эмпирические формулы. Определение параметров эмпирических формул методом наименьших квадратов
Постановка задачи. При экспериментальном изучении зависимости
y от x проводят ряд измерений величины y |
при различных значениях ве- |
||||
личины x. Результаты измерений (xi , yi ), |
i = |
|
записывают таблицей |
||
1, n |
|||||
либо точками на плоскости XOY. |
|
|
|
|
|
Рассмотрим следующую задачу: установить аналитическое выраже- |
|||||
ние зависимости y от |
x, т.е. найти непрерывную функцию |
y = f (x) та- |
|||
кую, чтобы yi = f (xi ) |
( yi ≈ f (xi )) . |
|
|
|
|
Функции, полученные при решении рассмотренных задач, называ- |
|||||
ются эмпирическими или аппроксимирующими. |
|
||||
Задача построения аппроксимирующей функции f(x) |
по экспери- |
||||
ментальным данным состоит из двух этапов: |
|
|
|
|
|
1)определение вида аппроксимирующей функции f(x), т.е. выбор класса функций (линейная, квадратичная, показательная, логарифмиче- ская…), к которому принадлежит аппроксимирующая функция;
2)определение параметров аппроксимирующей функции f(x) вы- бранного вида.
117

Определение вида аппроксимирующей функции
Не существует методов, которые теоретически обосновали выбор той или другой аппроксимирующей функции. Но при выборе аппроксими- рующей функции y = f (x) учитывают характер расположения экспери-
ментальных точек на плоскости. Так, если экспериментальные точки
(xi , yi ), i = 1, n расположены вдоль некоторой линии, например, вдоль пря-
мой, то в качестве аппроксимирующей функции выбирают f (x) = a0 + a1x ,
если расположение точек напоминает параболу, то в качестве аппроксими- рующей функции выбирают
f (x) = a0 + a1x + a2 x2 .
При выборе аппроксимирующей функции y = f (x) , если возможно,
проводят замену переменной, которая сводила бы нелинейную функцию к
линейной или параболической. Например, функцию |
y = a + |
b |
|
|
с помощью |
|||||||||||||||||||||
x |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
замены переменных |
z = y приводим к функции z = a + bt; y = |
1 |
|
|
. За- |
|||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a + bx |
||||||||
меной z = |
1 |
, |
t = x |
приводим к функции |
z = a + bt ; функцию |
|
y = |
|
x |
|
||||||||||||||||
|
|
a + bx |
||||||||||||||||||||||||
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
заменой z = |
x |
, |
t = x |
приводим к функции |
z = a + bt ; |
|
|
функцию |
||||||||||||||||||
|
|
|||||||||||||||||||||||||
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
y = ea +bx+cx2 |
с помощью замены |
z = ln y , t = x |
приводим к функции |
|||||||||||||||||||||||
y = a + bx + cx2 ; а функцию y = |
|
1 |
|
с помощью замены |
z = |
1 |
, |
|||||||||||||||||||
a + bx + cx2 |
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
||||||
t = x приводим к функции z = a + bx + cx2 ; |
функцию |
y = a + |
b |
+ |
c |
|
|
с по- |
||||||||||||||||||
|
x2 |
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
||||
мощью замены z = y , t = |
1 |
приводим к функции z = a + bx + cx2 . |
|
|
|
|
|
|||||||||||||||||||
x |
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Очень часто для приведения функции к линейному виду (или более простому по отношению к исходной функции) применяют операцию лога- рифмирования исходной функции.
Заметим, что при выборе аппроксимирующей функции следует учи- тывать характер расположения точек и тот процесс, который они описы- вают (масса, плотность, путь, скорость).
118
Нахождение коэффициентов (параметров) аппроксимирующей функции по методу наименьших квадратов
Пусть для данного эксперимента определен вид аппроксимирующей функции y = (x, a, b, c... p) .
Подбор параметров a, b, c... p этой функции по методу наименьших квадратов (МНК) проводится таким образом, чтобы сума квадратов откло- нений наблюдаемых значений yi от ординат аппроксимирующей функ-
ции была минимальной, т.е.
n
S= ∑( yi - j(x, a, b, c... p))2 = min .
i=1
Задача определения тех значений параметров a, b, c... p , при кото-
рых функция S (a, b, c... p) |
достигает минимума, сводится к решению сис- |
||
темы уравнений: |
|
|
|
∂S = 0, |
∂S = 0, |
∂S = 0 ... |
∂S = 0 . |
¶a |
¶b |
¶c |
¶p |
Рассмотрим методику определения параметров некоторых аппрок- симирующих функций по МНК.
1. Определение параметров для линейной аппроксимирующей функ- ции. Пусть точки в рассматриваемом эксперименте располагаются вдоль некоторой прямой линии. В этом случае в качестве аппроксимирующей функции выбираем линейную функцию ϕ(x) = a + bx . Коэффициенты a и
b выбираем таким образом, чтобы сума квадратов отклонений |
yi (i = |
1, n |
) |
из эксперимента от ординат аппроксимирующей функции |
ϕ(x) = a + bx |
||
была минимальной |
|
|
|
n
S= ∑( yi - a - bxi )2 = min .
i=1
Полученная функция S – функция двух переменных a и b, поэтому
для нахождения минимума функции |
S(a, b) |
необходимо приравнять к ну- |
|||
лю частные производные этой функции по a |
и b; |
||||
|
¶S = 0 |
n |
- a - bxi ) × (-1)) = 0 |
||
|
∑(2( yi |
||||
|
¶a |
|
i=1 |
|
|
|
¶S |
|
|
|
|
|
= 0 |
n |
|
|
|
|
¶b |
∑(2( yi |
- a - bxi ) × (-xi )) = 0 |
||
|
|
i=1 |
|
|
|
119
Из последней системы, после преобразования приходим к следую- щей системе уравнений относительно a и b
|
n × a |
n |
n |
|
+ b∑xi |
= ∑ yi |
|
|
|
i =1 |
i=1 |
|
n |
n |
n |
a × ∑x |
+ b∑x |
2 = ∑x y |
|
|
i |
i |
i i |
|
i=1 |
i=1 |
i=1 |
Решая полученную систему (например, методом Крамера) получим
aи b, а, следовательно, и ϕ(x) .
2.Определение параметров квадратичной аппроксимирующей функ- ции по МНК. Если точки в рассматриваемом эксперименте расположены вдоль некоторой параболы, то в качестве аппроксимирующей функции вы- бирают квадратичную зависимость
y = ax2 + bx + c ,
где a, b, c – постоянные, которые определяют, решая систему уравнений относительно a, b и c.
|
n |
4 |
n |
3 |
n |
2 |
n |
× x |
|
a∑x |
+ b∑x |
+ c∑x |
= ∑ y |
||||
i |
|
i |
i |
i |
i |
|||
i=1 |
|
i=1 |
|
i=1 |
|
i=1 |
|
|
|
n |
3 |
n |
2 |
n |
|
n |
|
a∑x |
+ b∑x |
+ c∑x |
= ∑x |
× y |
||||
|
|
i |
i |
|
i |
i |
i |
|
|
i=1 |
|
i =1 |
|
i =1 |
|
i=1 |
|
n n n
a∑xi2 + b∑xi + c × n = ∑ yi .
i=1 i =1 i=1
120
