
14-es / Высшая математика (РТФ) / умк_Цывис_Функции_Интеграл. исчисл
..pdf
Решение. Особые точки функции x = ±1. Первообразная ln x2 -1 обраща-
ется в ∞ в особых точках, следовательно данный интеграл не существует.
1 |
arcsin x |
|
|
|
Пример 17. Исследовать на сходимость интеграл I = ∫ |
|
dx . |
||
|
|
|
||
|
||||
0 |
1 - x2 |
|||
Решение. Особая точка функции x = 1: первообразная 1 (arcsin x)2 не-
|
|
2 |
прерывна в точке x = 1, значит, интеграл существует и |
I = |
p2 |
. |
||
|
|
8 |
|
|
1 |
Пример 18. Исследовать на сходимость интеграл |
I = ∫lnxdx . |
|
|
|
0 |
Решение. Особая точка подынтегральной функции x = 0: F (x) = x ln x - x
при x ® 0 имеет предел 0. Полагая, F(0) = 0, получим
1 |
|
1 |
|
||
|
|
|
I = ∫ln xdx = (x ln x - x) |
|
= -1. |
0 |
|
0 |
|
3. Признаки Коши существования несобственного интеграла II рода.
Если при достаточно близких k в значений x функция f(x) имеет вид
|
|
|
f (x) = |
g(x) |
(n > 0) , |
|
|
|
(b - x)n |
||
|
|
|
|
|
|
тогда: |
|
|
|
|
|
|
|
|
|
|
b |
1) |
при n < 1 |
и |
g(x) £ c £ +¥ , то интеграл ∫ f (x)dx сходится; |
||
|
|
|
|
|
a |
2) |
если n ³ 1 |
и |
g(x) ³ c > 0 , то этот интеграл расходится. |
||
На практике удобно использовать следующую форму признака Коши. Если при x ® b функция f(x) является бесконечно большой поряд-
|
1 |
b |
||
ка n > 0 (по сравнению с |
), то интеграл ∫ f (x)dx сходится или рас- |
|||
|
b - x |
|||
|
|
a |
||
ходится в зависимости от того, будет n < 1 или n > 1. |
||||
Если функция f(x) |
абсолютно интегрируема в промежутке [a;b), а |
|||
функция g(x) интегрируема на промежутке [a;b) в собственном смысле,
то функция f (x) × g(x) абсолютно интегрируема на [a;b).
1 |
|
dx |
|
|
Пример 19. Исследовать на сходимость интеграл I = ∫ |
|
|
. |
|
|
|
|
||
|
|
|||
0 |
1 - x4 |
|||
241
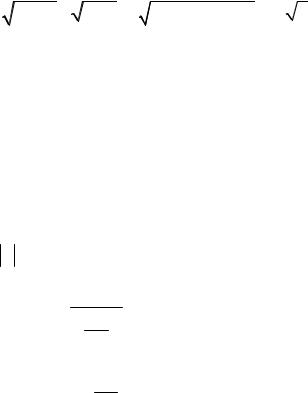
Решение. Так как справедливо соотношение |
|
|
|
|
|
||||||||||||||||
1 |
|
: |
1 |
|
|
= |
1 |
|
|
→ |
1 |
|
при x → 1 , |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
4 1 − x4 |
4 1 − x |
|
|
|
4 4 |
|||||||||||||
|
|
|
|
|
|
4 1 + x + x2 + x3 |
|
|
|||||||||||||
то подынтегральная функция при x → 1 |
есть бесконечно большая порядка |
||||||||||||||||||||
|
1 |
. Следовательно, искомый интеграл сходится. |
|
|
|||||||||||||||||
4 |
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
Пример 20. Исследовать на сходимость |
I = ∫ xn ln xdx . |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
Решение. 1. Если n > 0, то |
|
f (x) = x4 ln x → 0 при |
|
x → 0 данный интеграл |
|||||||||||||||||
Iсуществует как собственный, т.е. сходится.
2.Если n > –1, то выбирая m удовлетворяющих условно выраже-
нию 1 > m > n = −n , будем иметь
x n ln x = xn+ n ln x → 0 при x → 0 , 1
xm
1 dx
а так как интеграл ∫ сходится, то и исходный интеграл I будет
0 xm
сходиться.
1
3. Если n ≤ −1, то интеграл ∫ xndx расходится, а значит и исходный
0
интеграл расходится.
Пример 21. Исследовать на сходимость интегралы:
1 |
π |
|
sin |
n−1 |
xdx |
|
|||
1. I = ∫ xn−1(1 − x)m−1dx ; |
2. I = ∫ |
|
|
|
. |
||||
|
|
|
|
|
|||||
0 |
0 |
|
|
1 + k cos x |
|
n |
|||
|
|
||||||||
Решение. 1. Если n < 1, то особая точка x = 0, при m < 1 особая точка x = 1. Данный интеграл разбиваем на два, например
|
1 |
|
|
|
|
1 |
2 |
|
1 |
|
|
I = ∫ xn−1(1 − x)m−1dx = ∫ xn−1(1 |
− x)m−1dx + ∫ xn−1(1 − x)m−1dx . |
||||
0 |
0 |
|
|
1 |
|
|
|
|
2 |
|
|
Так как подынтегральная функция при x → 0 есть бесконечно боль- шая (если n < 1) порядка (1 – n), то первый интеграл существует при ус- ловии (1 – n) < 1, т.е. n > 0. Аналогично, второй интеграл существует при
242

m > 0. Таким образом, исходный интеграл сходится тогда и только тогда, если одновременно n > 0 и m > 0.
2.Данный интеграл сходится, если
1)0 ≤ k < 1 и n > 0;
2)k > 1 и 0 < n < 1;
3)в других случаях данный интеграл расходится.
4.Интегрирование по частям.
Пусть функции n(x) |
и v(x) определены на промежутке [a;b) , имеют |
|||||||||||||||||||
непрерывные производные на отрезке |
[ac] для любого |
|
|
c (ab) . Если |
||||||||||||||||
существует конечный предел |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
lim |
(u(c) × v(c)) = u(b - 0) × v(b - 0) , |
|
|
(1) |
|||||||||||||||
|
c→b−a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
интеграл ∫vu¢dx сходится, то и интеграл |
|
∫uv¢dx |
сходится и справедлива |
|||||||||||||||||
a |
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
формула |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
b |
b |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
∫uv¢dx = uv |
|
- ∫v ×u¢dx . |
|
|
|
|
(2) |
|||||||||||
|
|
a |
|
a |
a |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Замечание. Если предел (1) конечный, то несобственные интегралы |
||||||||||||||||||||
|
|
b |
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
∫uv¢dx и |
∫vu¢dx |
|
|
|
|
|
|
|
|
|
||||||||
|
|
a |
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
сходятся или расходятся одновременно. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Пример 22. Вычислить интегралы |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
1 |
|
|
ln x |
|
|
|
|
|
1 |
|
ln xdx |
|
|
|||||
1. I = |
∫ ln sin xdx ; |
2. I = ∫ |
|
; |
|
3. |
I = ∫ |
|
|
. |
||||||||||
|
|
|
|
|
|
|
|
|||||||||||||
|
0 |
0 1 + x2 |
|
|
|
|
|
0 1 - x2 |
||||||||||||
|
π |
|
π |
|
π |
|
|
|
|
π |
|
|
|
|
|
|
|
|||
|
2 |
|
|
2 |
|
|
cos x |
|
2 |
x |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Решение. 1. |
I = ∫ ln sin xdx = x ln sin x |
02 |
- |
∫ x |
|
|
dx |
= - |
∫ |
|
|
dx . |
||||||||
|
|
|
|
|||||||||||||||||
|
0 |
|
|
|
|
|
0 |
|
|
sin x |
|
0 |
tgx |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Интегрированием по частям удалось свести несобственный интеграл к собственному и, тем самым, доказать существование исходного интеграла.
2. Аналогично, как и для случая 1 имеем
243

1 |
ln x |
1 |
|
1 |
1 arctgx |
1 arctgx |
|||
|
|
|
|||||||
I = ∫ |
|
= ∫ln xarctgx = ln x × arctgx |
|
|
- ∫ |
|
dx = -∫ |
|
dx . |
1 + x2 |
|
0 |
|
|
|||||
0 |
0 |
|
0 |
x |
0 |
x |
|||
|
|||||||||
Следовательно, данный интеграл сходится.
3. Аналогично, интегрируя по частям, имеем, что
1 |
ln xdx |
1 |
arcsin x |
|
||
I = ∫ |
|
= -∫ |
dx |
|||
|
|
|
|
|||
|
1 - x2 |
|||||
0 |
|
0 |
x |
|||
интеграл собственный, а следовательно, исходный интеграл сходится.
5. Замена переменной.
Если функция f(x) непрерывна на промежутке [a;b), |
а функция |
|||||||||||||||
x = ϕ(t) непрерывно дифференцируема на промежутке [a,b) , |
строго воз- |
|||||||||||||||
растает и удовлетворяет условиям |
ϕ(α) = a, lim |
ϕ(t) = b , то справедлива |
||||||||||||||
|
|
|
|
|
|
|
|
t →β−0 |
|
|
|
|
|
|
||
формула замены переменной |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
b |
β |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
∫ f (x)dx = ∫ f (j(t))j¢(t)dt |
|
|
(1) |
|||||||||||
|
|
a |
α |
|
|
|
|
|
|
|
|
|
|
|
||
при условии, что хотя бы один из интегралов в уравнении (1) сходится. |
||||||||||||||||
Пример 23. Вычислить интеграл |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
b |
dx |
1 |
|
exdx |
2 |
|
dx |
|||||||||
1. I = ∫ |
|
|
|
; |
2. ∫ |
|
|
|
|
; |
3. I = ∫ |
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
||||||
a |
(x - a)(x - b) |
0 1 - x2 |
0 |
|
|
tgx |
||||||||||
Решение. 1. Применяя подстановку |
x = a cos2 j + bsin2 j , приводим ис- |
|||||||||||||||
комый интеграл к собственному интегралу |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I = |
2 ∫ dj = p. |
|
|
|
|
|
|
|||||
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
2. Применяя подстановку x = sin t (a = 0, b = 1, a = 0, b = π ), полу- 2
чим собственный интеграл
π
2
I = ∫ esin t dt ,
0
а следовательно, искомый интеграл сходится.
244
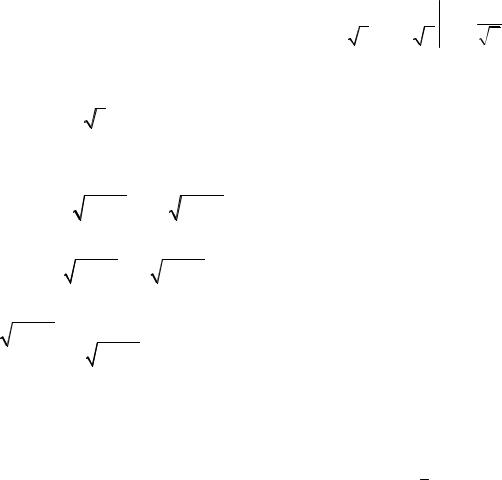
3. Для вычисления данного интеграла полагают t = tg x, т.е. x = arctgt
( a = 0, b = π , a = 0, b = +¥ ), тогда получаем уравнение
2
+∞ |
dt |
|
|
I = 2 ∫ |
. |
||
1 + t 4 |
|||
0 |
|
Для нахождения данного интеграла отметим следующее:
+∞ |
x |
2dx |
|
x = |
1 |
;a = +¥;b = 0 |
+∞ |
dt |
|
|
|
|
|
||||||||
∫ |
|
|
= |
|
t |
= ∫ |
|
. |
||
1 + x4 |
1 + t2 |
|||||||||
0 |
|
a = 0;b = +¥ |
0 |
|
||||||
|
|
|
|
|
|
|
||||
Тогда
+∞ |
|
2 |
|
+∞ |
(1 + |
1 |
|
)dx |
|
|
|
|
|
+∞ |
|
|
|
|
|
|
|
|
|
||||||||
(1 + x |
)dx |
x2 |
|
1 |
|
|
|
dt |
|
1 |
|
|
t |
||||||||||||||||||
2 × I = ∫ |
|
= ∫ |
|
|
|
|
|
|
|
= |
|
t = x - |
|
= |
∫ |
|
|
= |
|
arctg |
|||||||||||
1 + x4 |
|
|
|
|
|
|
|
1 |
|
|
x |
|
|
2 |
+ 2 |
|
|
|
|
|
|||||||||||
0 |
0 |
|
|
2 |
|
|
|
|
|
|
|
|
−∞ t |
|
2 |
2 |
|||||||||||||||
x |
|
|
|
+ x2 |
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Следовательно, |
I = |
|
π |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Пример 24. Доказать формулы
+∞
−∞
= p . 
 2
2
|
1 |
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
||||||
1. |
∫ |
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
(a >1) . |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
−1 (a2 |
- x2 ) × 1 - x2 a × a2 -1 |
|
|||||||||||||||||||||
|
1 |
|
|
dx |
|
|
|
|
= |
|
|
|
|
p |
|
|
|
|
(a > 0) . |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
2. |
∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
+ a2 ) 1 - x2 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
−1 (x2 |
|
|
|
|
a 1 + a2 |
|
|||||||||||||||||
Для доказательства |
|
можно |
использовать, например, |
подстановку |
||||||||||||||||||||
|
|
|
|
|
|
|
|
−x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Абеля u = ( 1 - x2 )¢ = |
|
|
|
|
|
. |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
1 - x2 |
|
|
|
|
|
|
+∞ |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Замечание 1. Интеграл с бесконечным пределом ∫ f (x)dx |
всегда с по- |
|||||||||||||||||||||||
a
мощью надлежащей подстановки приводится к интегралу с конечными предела-
ми (собственному или нет). Так, например, если a > 0, то, полагая x = 1 , получим t
+∞ |
1 |
|
|
|
|
|
|
a |
|
1 |
|
dt |
|
||
∫ f (x)dx = ∫ |
f ( |
) |
. |
||||
|
|
||||||
a |
0 |
|
t t 2 |
||||
245

b
Замечание 2. Несобственный интеграл ∫ f (x)dx с единственной осо-
a
бой точкой b всегда может быть приведен к интегралу с бесконечным пре-
делом (без других особых точек). Так, например, полагая x = b - 1 , получим t
b |
∞ |
|
1 |
|
dt |
|
|
∫ f (x)dx = ∫ |
f (b - |
) |
. |
||||
|
|
||||||
a |
1 |
|
t t2 |
||||
b−a
7.5. Особые приемы вычисления несобственных интегралов
Приведем примеры некоторых замечательных интегралов.
π
2
1. |
Интеграл Эйлера I = ∫ ln sin xdx . |
|
||
|
|
0 |
|
|
Ранее было установлено, что данный интеграл сходится. Вычислим |
||||
его, используя замену переменных, полагая x = 2t |
|
|||
|
π |
|
π |
π |
|
4 |
|
4 |
4 |
|
I = 2 ∫ ln sin 2tdt = p ln 2 + 2 |
∫ ln sin tdt + |
2 ∫ ln costdt . |
|
|
0 |
2 |
0 |
0 |
|
|
|||
В последнем интеграле положим t = π - u , приведем его к виду |
||||
π |
|
|
2 |
|
|
|
получим уравнение I = π ln 2 + 2I , |
||
2 |
|
|
||
2 × ∫ ln sin udu , тогда для определения I |
||||
π |
|
|
|
2 |
4 |
I = - π ln 2 . К этому же интегралу, с точностью до знака приводят- |
|||
откуда |
||||
|
2 |
|
|
|
ся и собственные интегралы:
π
2 |
|
x |
1 arcsin x |
|
|
|
|
|
||||
∫ |
|
|
dx, |
∫ |
|
|
dx . |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
tgx |
|
x |
|
|
|
|
|
|||||
0 |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|||
2. Интеграл Эйлера – |
Пуассона |
|
I = ∫ e− x |
2 dx = |
|
. |
||||||
|
|
|
||||||||||
|
|
|
|
|
0 |
|
|
2 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
||
246

|
|
|
+∞ |
f (ax) - f (bx) |
|
|
|||||
3. Интегралы Фруллани |
I = ∫ |
|
|
|
|
|
|
(a,b > 0) |
|||
|
x |
|
|
|
|||||||
|
|
|
0 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
Считаем, что: 1) функция f(x) определена и непрерывна для x ³ 0 и |
|||||||||||
2) существует конечный предел |
lim |
f (x) = f (+∞) . |
|
|
|||||||
+∞ |
|
|
x→+∞ |
|
|
|
|
|
|
|
|
f (ax) - f (bx) |
= ( f (0) - f (+¥)) × ln |
b |
|
|
|||||||
Тогда ∫ |
|
|
. |
|
|
||||||
x |
|
|
|
||||||||
0 |
|
|
|
|
|
a |
|
|
|||
|
|
|
|
+∞ e−ax - e−bx |
|||||||
|
|
|
|
|
|||||||
Пример 25. Вычислить интеграл I = ∫ |
|
|
|
|
|
dx . |
|||||
|
|
x |
|
||||||||
|
|
|
|
|
0 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
Решение. В данном случае имеем f (x) = e− x , f (0) =1, f (+¥) = 0 , тогда I = ln b . a
+∞ arctgax - arctgbx |
|
||
Пример 26. Вычислить интеграл I = ∫ |
|
dx . |
|
x |
|||
0 |
|
||
|
|
||
Решение. В данном случае имеем f (x) = arctgx, f (0) = 0, f (+¥) = π . 2
Тогда I = π ln a . 2 b
Замечание 1. Отметим, что если функция f(x) не имеет конечного пре-
|
|
+∞ f (t) |
|
|
|
|
|
+∞ |
f (ax) - f (bx) |
= f (0) |
× ln |
b |
||||||||||
дела при x → +∞ , но существует ∫ |
|
|
|
dt , то |
∫ |
|
|
|
|
|
. |
|||||||||||
|
|
|
|
|
x |
|
||||||||||||||||
|
|
a |
t |
|
|
|
|
|
0 |
|
|
|
|
|
a |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
+∞ cos ax - cosbx |
|
|
|
|
|
|
b |
|
|
|
+∞ cost |
|
|
|
||||||||
Например, I = ∫ |
|
|
|
dx = ln |
|
. |
Интеграл ∫ |
|
|
dt |
суще- |
|||||||||||
|
x |
|
|
|
||||||||||||||||||
0 |
|
|
|
|
|
|
|
a |
|
|
|
a |
t |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
ствует, хотя f(x) = cos x |
при x → +∞ конечного предела не имеет (предел |
|||||||||||||||||||||
не существует). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Замечание 2. Аналогично, если нарушена непрерывность функции |
||||||||||||||||||||||
|
|
|
|
|
|
a |
|
f (t) |
|
|
|
(a < +¥) . Тогда |
|
|
|
|||||||
f(x) при x = 0 , но существует интеграл ∫ |
|
|
|
|
|
dt |
|
|
|
|
|
|||||||||||
|
t |
|
|
|
||||||||||||||||||
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
+∞ |
f (ax) - f (bx) |
|
|
|
|
|
|
|
a |
|
|
|
|
|
||||||||
∫ |
|
|
|
dx = f (+¥)ln |
|
. |
|
|
|
|
|
|||||||||||
x |
|
|
|
|
|
|
|
|||||||||||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Используя замену переменной |
|
x = |
1 |
, приходим к замечанию 1. |
|
|
|
|||||||||||||||
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
247
§ 8. Интегрирование как процесс суммирования.
Приложения определенного интеграла
До сих пор процесс интегрирования рассматривался как процесс, об- ратный дифференцированию. Это была одна сторона дела, если можно сказать, чисто математическая, в большей степени формальная. Другая сторона, и притом несравненно более значимая для разнообразных приме- нений интегрального исчисления к естествознанию, это, то обстоятельство, что интегральное исчисление дает эффективный способ находить пределы сумм бесконечно увеличивающегося числа бесконечно уменьшающихся слагаемых. Еще до Ньютона решение ряда проблем естествознания своди- лись к отысканию пределов таких сумм, потом все это было систематизи- ровано. Таким образом, самой жизнью было востребовано интегральное исчисление несколько раньше, чем дифференциальное исчисление. С этой точки зрения интегральное исчисление получает вид уже не исчисления, обратного дифференцированию, а процесса суммирования.
Две эти стороны интегрального исчисления тесно переплетаются ме- жду собой и, без процесса дифференцирования, интегральное исчисление как процесс суммирования не много бы стоил. Это действительно так, по- тому, что процесс суммирования – это процесс не прямой, а косвенный.
Прямым образом находить пределы сумм удается в крайне редких случаях. Так как решена проблема обратная дифференцированию, т.е. на-
хождение неопределенного интеграла ∫ f (x)dx , то естественно и решается задача суммирования, как предел суммы
f (x0 )Dx0 + f (x1 ) × Dx1 + ... + f (xn −1 ) × Dxn −1 ,
где x0 = a, xn = b и n → +∞ при Dxi ® 0 |
равен определенному интегралу |
b |
|
∫ f (x)dx . |
(1) |
a |
|
Таким образом, вся эффективность интегрального исчисления осно- вана на возможности находить определенный интеграл (1), не производя никаких переходов к пределу.
248
8.1. Общая схема применения интегрального исчисления
Разнообразные вопросы естествознания (физика, химия, механика, геометрия) являются постоянными источниками, дающими задачи для применения интегрального исчисления.
Так как математика изучает объекты любой природы, то естественно ожидается, что и применение интегрального исчисления будет иметь одну
иту же схему. Эта схема имеет следующую структуру:
1.Пусть при изучении некоторого процесса требуется определить некоторую величину V.
2.Разбиваем V на большое число мелких частей и представляем каждую из полученных частей в виде произведения
f (ci ) × Dxi ,
где f(x) – функция известная нам и непрерывна; ci Î[xi −1xi ].
3. Получаем равенство вида (интегральная сумма)
|
|
n |
|
|
V = ∑ f (ci ) xi , |
|
|
|
|
i =1 |
|
где x0 = a, xn = b . |
|
|
|
4. |
Переходим к пределу при max Dxi |
® 0 находим выражение ис- |
|
комой величины V в виде определенного интеграла |
|||
|
V = lim |
n |
b |
|
∑ f (ci ) xi = ∫ f (x)dx . |
||
|
max xi |
→0 i =1 |
a |
5. |
Если найти неопределенный интеграл ∫ f (x)dx , то искомую ве- |
||
личину V определим по формуле Ньютона-Лейбница.
8.2. Вычисление площадей плоских фигур
Обычно, при рассмотрении понятия площади плоской фигуры F, го- ворят, что площадь S(F) данной фигуры F есть число, показывающее из скольких единиц площади «составлена» эта фигура (за единицу площади принимается квадрат, сторона которого равна единице длины). Однако та- кое наглядное и доступное пояснение не может служить точным матема- тическим определением понятия площади плоской фигуры. Например, не- ясно каким образом из единиц площади (квадрат со стороной равной еди- нице длины) «составляется» круг заданного радиуса.
249

F
Рис. 1
Один из способов уточнения по- нятия площади основывается на рас- смотрении палетки – разбиение плоско- сти на равные квадраты. Так, если сто- рона квадрата палетки имеет длину 1, то на рис. 1 фигура F содержит фигуру, составленную из квадратов палетки, и содержится в фигуре, составленной из квадратов, поэтому имеем
9 ≤ S (F ) ≤ 29 .
Для более точной оценки можно использовать палетку, квадраты ко- торой имеют стороны длиной 0,1 (так, что в каждом квадрате прежней па- летки содержится 100 квадратов новой палетки). Так, если F содержит фигуру, составленную из 1716 квадратов новой палетки, и содержится в фигуре, составленной из 2025 таких квадратов, то 17,16 < S (F ) ≤ 20,25 .
Уменьшая в 10 раз длину стороны палетки, т.е. еще раз измельчая палетку, можно еще точнее оценить S(F) и т.д. Рассмотренный процесс измельче- ния используется не только для вычисления площади фигуры, но и для са- мого определения понятия площади.
Действительно, рассмотрим палетку, длины сторон которой равны
|
1 |
. Если |
F содержит фигуру, составленную из |
an квадратов этой палет- |
||||||||||
10n |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
ки, и содержится в фигуре, составленной из bn |
таких квадратов, тогда |
|||||||||||||
|
an |
|
есть значение площади фигуры F с недостатком, а |
bn |
– значение |
|||||||||
102n |
|
|||||||||||||
|
|
|
|
|
|
|
|
102n |
|
|||||
площади – |
с избытком. |
|
|
|
|
|
|
|
|
|||||
|
|
|
Неограниченно увеличивая n |
|
(n → ∞) , рассмотрим пределы |
|||||||||
|
|
|
|
S (F ) = lim |
an |
; |
|
|
(F ) = lim |
bn |
. |
|
|
|
|
|
|
|
|
S |
|
|
|||||||
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
n →∞ 102n |
|
|
|
n →∞ 102n |
|
|
|
|||
Первый, из которых называют нижней, а второй – верхней площадью фигуры F.
Если для фигуры F эти пределы совпадают, то фигура F называет- ся квадрируемой, а число S (F ) = S (F ) = S (F ) называется площадью фи-
гуры F и обозначается S(F).
Отметим, что любой многоугольник является квадрируемой фигурой, точно так же как и любая выпуклая фигура (в частности круг) квадрируе- ма. Следовательно, можно сказать, что площадь S(F) есть неотрицательная
250
