
14-es / Высшая математика (РТФ) / умк_Цывис_Функции_Интеграл. исчисл
..pdf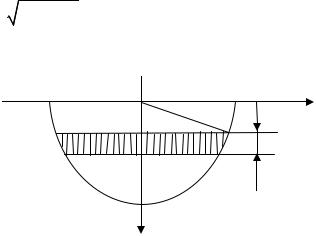
Тогда
R |
|
R |
|
1 |
|
2 |
|
||
|
|
|
|
|
|
||||
P = γ ∫ 2x R2 − x2 dx = −γ ∫ |
(R2 − x2 ) |
2 |
d (R2 − x2 ) = |
γR3 . |
|||||
|
|||||||||
0 |
0 |
|
3 |
|
|||||
|
|
|
|
|
|
||||
|
|
R |
0 |
|
|
y |
|||
|
|
x |
|
R |
|||||
dx
x
Пример 42. Вычислить работу, которую необходимо затратить, что- бы выкачать жидкость из цилиндрической цистерны, радиус основания ра- вен R, а высота h (γ – плотность жидкости).
Решение. Разобьем объем цилиндра плоскостями, параллельными основа- нию, расстояние между которыми равно dx. Тогда объем полученного элемента объема – цилиндра будет равен
dV = πR2 dx ,
а численная величина массы – g × pR2dx .
Тогда элементарная работа dA, затраченная на поднятие этой массы, находящейся на глубине x будет равна
dA = x × gpR2 dx .
А величина работы
|
h |
|
|
γπR2 h2 |
A = γπR2 ∫ xdx = |
. |
|||
|
0 |
|
|
2 |
|
|
|
|
|
Пример43. Определить количество тепла, выделяемое переменным током |
||||
|
|
2π |
|
|
I = I |
0 |
|
t |
− ϕ |
|
||||
|
|
T |
|
|
в течение периода Т в проводнике с сопротивлением R.
Решение. Количество тепла в единицу времени для постоянного тока оп- ределяется законом Джоуля – Ленца
Q = 0, 24I 2 R .
291

Для переменного тока элемент (дифференциал) количества тепла бу- дет равен
dQ = 0,24I 2 (t)Rdt .
Тогда
2 |
T |
2 |
2p |
|
2 |
|
|
||||||
Q = 0, 24RI0 |
∫sin |
|
|
|
t - j dt = 0,12RTI0 . |
|
|
|
|||||
|
0 |
|
T |
|
|
|
|
|
|
|
|
|
|
Путь, пройденный материальной точкой. Если точка движется по некоторой кривой и величина ее скорости известная функция v = f (t) вре-
мени t, то путь, пройденный точкой за промежуток времени [t1,t2 ] равен
t2
S = ∫ f (t)dt .
t1
Работа переменной силы. Если переменная сила ет в направлении оси Ox, то работа этой силы на отрезке
x2
A = ∫ f (x)dx .
x1
F = f(x) действу- [x1, x2 ] равна
Статистические моменты, моменты инерции и координаты центра масс плоской линии. Пусть плоская кривая АВ задана уравне-
ниями y = f (x), x Î[ab] , плотность которой ρ = ρ(x) , тогда
- масса кривой определяется по формуле
b
M = ∫r 1 + ( y¢)2 dx ;
a
- статические моменты относительно оси Ox и Oy:
|
b |
|
|
|
b |
|
|
|
M x = ∫r × y 1 + ( y¢)2 dx, M y = ∫r × x 1 + ( y¢)2 dx; |
||||||||
|
a |
|
|
a |
||||
- моменты инерции |
I x , I y , I0 – относительно оси Ox, Oy и точки О: |
|||||||
b |
|
|
b |
|
|
|||
I x = ∫ry2 1 + ( y¢)2 dx , I y = ∫rx2 1 + ( y¢)2 dx , I0 = I x + I y ; |
||||||||
a |
|
a |
||||||
292
- координаты центра масс кривой:
|
x = |
M y |
; y |
= |
M |
x |
. |
|
|
|
|
||||
|
c |
M |
c |
|
M |
||
|
|
|
|
||||
Статистические моменты, моменты инерции и координаты цен- |
|||||||
тра масс плоской фигуры. |
Пусть дана криволинейная трапеция, ограни- |
||||||
ченная графиком функции |
y = f (x) ³ 0, |
x Î[ab] , осью Ox и прямыми x = |
|||||
aи x = b; ρ – плотность. Тогда
-масса криволинейной трапеции
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
||
|
|
|
|
|
|
|
M = ∫rydx ; |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
||
- моменты инерции |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
1 |
b |
|
|
|
|
|
|
|
|
|
b |
||
M x |
= |
∫ry2 dx, |
|
M y |
= ∫rxydx ; |
||||||||||||
|
|
||||||||||||||||
|
|
|
2 |
a |
|
|
|
|
|
|
|
|
|
a |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
- моменты инерции |
|
I x , |
I y , I0 |
|
|
|
|
|
|
|
|
||||||
|
1 |
b |
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
I x = |
∫ry3dx; I y |
= |
∫rx2 ydx; I0 = I x + I y |
||||||||||||||
|
|||||||||||||||||
2 |
a |
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
- координаты центра масс плоской фигуры |
|||||||||||||||||
|
|
|
|
x |
|
= |
|
M y |
; |
y = |
M |
x |
. |
||||
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
c |
|
|
M |
|
|
c |
|
M |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Теорема Гульдена.
1. Площадь поверхности, полученной от вращения дуги плоской кривой вокруг некоторой оси, лежащей в одной плоскости с кривой и ее непересекающей, равна произведению длины дуги на длину окружности, описываемой центром тяжести дуги кривой;
2. Объем тела, полученного при вращении плоской фигуры вокруг некоторой оси, лежащей в плоскости фигуры и ее не пересекающей, равен произведению площади этой фигуры на длину окружности, описываемой центром тяжести фигуры.
293

§ 9. Приближенное вычисление определенных интегралов
9.1. Постановка задачи
Пусть требуется вычислить определенный интеграл
b |
|
I = ∫ f (x)dx |
(1) |
a |
|
Если функция f(x) непрерывна на отрезке |
[a,b] и известна первооб- |
разная F(x), то определенный интеграл I можно вычислить по формуле Ньютона – Лейбница. Но в ряде случаев бывает невозможно найти перво- образную F(x) по ряду причин: либо F(x) не выражается через элемен- тарные функции, либо выражается достаточно сложно. В этих случаях оп- ределенный интеграл вычисляют приближенно. Здесь будут рассмотрены основные способы приближенного вычисления определенных интегралов, суть которых основана на одном и том же приеме: отрезок интегрирования разбивается на части, в соответствии с чем, криволинейная трапеция раз- бивается на сумму частичных криволинейных трапеций; каждая из по- следних заменяется достаточно близкой к ней фигурой, площадь которой может быть достаточно просто вычислена, тогда сумма площадей этих фи- гур выражает приближенно площадь искомой криволинейной трапеции, т.е. рассматриваемый определенный интеграл.
9.2. Формула прямоугольников
Будем считать в формуле (1), что f(x) непрерывна и для простоты рассуждений ограничимся случаем, когда f (x) ³ 0 и, выбирая в качестве фигуры, заменяющей частичную криволинейную трапецию прямоугольни- ком с тем же основанием и с какой-нибудь из восстановленных к нему ор- динат в качестве высоты, мы заменим определенный интеграл (1) соответ- ствующей интегральной суммой. Разбивая отрезок интегрирования на дос- таточно мелкие части, мы, таким образом, получим значение интеграла по определению с любой степенью точности.
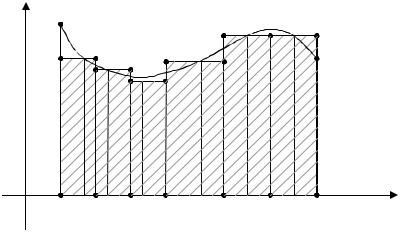
Разобьем отрезок [a,b] на n равных частичных отрезков точками xk
(рис. 1)
xk = a + b − a , k = 1, n − 1; n
длина каждого из x |
= x |
− x |
= |
b − a |
. |
|
|||||
k |
k |
k −1 |
|
n |
|
|
|
|
|
||
294
y
A
y = f(x)
B
|
|
|
|
a = x0 c1 x1 |
xk −1 |
|
ck xk |
|
b = xn |
|
x |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
Рис. 1 |
|
|
|
|
|
|
|
|
|||||
|
|
На |
каждом |
частичном |
отрезке |
[ xk −1, xk ] выбираем |
точку |
||||||||||||||||
c = |
xk − xk −1 |
и вычислим значения |
y |
k |
= f (c |
) . Тогда имеем |
|
||||||||||||||||
|
|
||||||||||||||||||||||
k |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
b |
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∫ f (x)dx = |
lim |
∑ f (ck ) × xk , т.е |
|
|
|
|
||||||||||||
|
|
|
|
|
a |
|
|
xk →0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
(n →∞) k =1 |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
b |
n |
|
|
b - a |
|
|
b - a |
|
|
|
b - a |
|
|
b - a |
|
n |
||||||
|
∫ f (x)dx » ∑ f (ck ) |
× Dxk |
» |
y1 + |
y2 + ... + |
yn |
= |
× ∑ yk . |
|||||||||||||||
|
n |
|
|
|
|
||||||||||||||||||
|
a |
k =1 |
|
|
|
|
|
|
n |
|
|
|
|
|
n |
|
n |
k =1 |
|||||
|
|
Следовательно |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
b |
|
b - a |
|
|
n |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
∫ f (x)dx » |
× |
∑ yk , |
|
|
|
(2) |
|||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
a |
|
|
|
|
n |
|
|
|
k =1 |
|
|
|
|
|
|
|
|
т.е. площадь криволинейной трапеции aABb приближенно равна площади ступенчатой фигуры, заштрихованной на рис. 1.
Формула (2) – формула прямоугольников. Отметим, что если суще-
ствует непрерывная вторая производная |
|
f |
′′ |
на |
[a,b], то погрешность |
|||||
|
|
(x) |
||||||||
формулы (2) при вычислении интеграла (1) оценивается неравенством |
||||||||||
D(n) £ sup |
|
f ¢¢(x) |
|
× |
(b - a)3 |
|
(3) |
|||
|
|
|||||||||
|
|
|
||||||||
[ab] |
|
|
|
|
|
|
24n2 |
|
||
|
|
|
|
|
|
|||||
Если задана погрешность вычисления |
|
(n) , |
то, используя неравен- |
|||||||
ство (3), можно построить такое разбиение отрезка |
[a,b] на n частей, при |
|||||||||
295
котором приближенное вычисление определенного интеграла (1) будет выполнено с точностью, не превышающей заданную.
Если погрешность вычисления не задана, то при фиксированном n можно оценить ее по формуле (3).
9.3. Формула трапеций
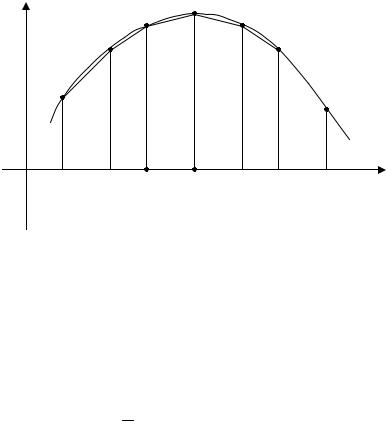
Данный способ, который мы изложим, основан на замене каждой частичной криволинейной трапеции прямоугольной трапецией с теми же вершинами (рис. 2)
y
y = f(x)
A
B
a |
xk −1 xk |
b |
x |
Рис. 2
Площадь такой трапеции равна |
1 |
( y |
k −1 |
+ y |
|
) × Dx , где |
y |
|
= f (x ) , |
|
k |
k |
|||||||
|
2 |
|
|
k |
|
k |
|||
|
|
|
|
|
|
|
|
|
xk = xk − xk −1 .
Таким образом, искомый интеграл (1) заменим суммой вида
1∑n ( yk −1 + yk ) × Dxk .
2k =1
|
Если |
отрезок интегрирования |
[a,b] разбиваем |
на равные |
части |
|||||||
Dx = |
b − a |
, то получим приближенное равенство |
|
|
|
|||||||
|
|
|
|
|||||||||
k |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
b |
f (x)dx » |
y0 |
+ yn |
+ y1 |
+ y2 + ... + yn −1 × |
b - a |
|
|
|
|
|
|
∫ |
. |
(4) |
|||||||
|
|
|
|
2 |
|
|||||||
|
|
|
a |
|
|
|
n |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Приближенное равенство (4) называется формулой трапеций.
296

Оценим погрешность, получающуюся при вычислении интеграла по формуле трапеций.
Пусть |
′ |
и |
f |
′′ |
существуют и непрерывны |
для любого |
|||
f (x) |
(x) |
||||||||
x [a,b] . Рассмотрим криволинейную трапецию с основанием |
(xk −1, xk ) . |
||||||||
Пусть |
xk −1 + xk |
|
= C |
|
xk |
− xk −1 |
= h . |
|
|
2 |
|
|
|
|
2 |
|
|||
|
|
|
|
|
|
|
|
||
Тогда |
xk −1 = c − h |
xk +1 = c + h . |
|
||||||
Рассмотрим функции ψ(t) и ϕ(t) :
c +t |
|
ψ(t) = ∫ f (x)dx − t [ f (c + t) + f (c − t)], |
|
c −t |
|
ϕ(t) = ψ(t) − t2 |
ψ(h) . |
h3 |
|
ψ(h) есть разность площадей криволинейной и прямоугольной трапеций.
Дифференцируя ϕ(t) и применяя теорему о конечном приращении, получим
ϕ′(t) = −t [ f ′(c + t) − f ′(c − t)] − |
3t2 |
|
|
3 |
|
|
|
|
|
|
ψ(h) = −2t2 |
f ′′(ςi ) + |
|
|
ψ(t) |
, |
|
h |
3 |
2h |
3 |
|||||
|
|
|
|
|
|
|
||
где ςi (c − t, c + t) .
Так как ϕ(0) = ϕ(h) = 0 , то существует такое значение t = τ, τ (0; h) ,
что ϕ′(τ) = 0 , тогда для значения ςi , соответствующего этому τ , будем иметь
ψ(h) = − 2h2 f ′′(ςi ) 3
или из определения функции ϕ(t) :
|
∫ f (x)dx − 1 ( yk + yk −1 ) b − a = − (b − a) |
|
f ′′(ςi ) . |
|||||||||||||||||||
|
xk |
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
||
|
xk −1 |
|
|
2 |
|
|
n |
|
12n3 |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Учитывая в последнем равенстве, что h = |
b − a |
|
k = |
|
, затем |
|||||||||||||||||
и |
1, n |
|||||||||||||||||||||
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2n |
|
|
|
|||||
суммируя их, получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
b |
|
y + y |
n |
|
|
|
|
b − a |
|
|
(b − a)3 |
n |
||||||||||
∫ f (x)dx − |
|
0 |
+ y1 + y2 |
+ ... + yn −1 |
|
= − |
|
|
|
|
∑ f ′′(ςi ) . |
|||||||||||
|
2 |
|
|
|
|
12n3 |
||||||||||||||||
a |
|
|
|
|
|
|
n |
|
|
|
|
i =1 |
||||||||||
297
Среднее арифметическое лежит между наибольшим и наименьшим
|
|
|
1 |
n |
|
|
|
|
|
|
|
|
|
|
|
|
значениями, тогда |
∑ f ′′(ςi ) находится между наибольшим и наимень- |
|||||||||||||||
|
||||||||||||||||
|
|
|
n i =1 |
|
|
|
|
|
|
|
|
|
|
|||
шим значениями |
f |
′′ |
|
|
|
|
|
′′ |
непрерывна, то существует ς |
|||||||
(x) , а так как |
f (x) |
|||||||||||||||
такое, что |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
1 |
n |
′′(ςi ) = f ′′(ς) . |
|
|
|
|||||
|
|
|
|
|
|
∑ f |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
n i =1 |
|
|
|
|
|
|
|
||
Тогда получим оценку погрешности |
|
|
|
|
|
|||||||||||
b |
|
y + y |
n |
|
|
|
|
|
b − a |
|
(b − a)3 |
′′ |
||||
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|||
∫ |
f (x)dx − |
|
|
|
|
+ y1 |
+ y2 |
+ ... + yn −1 |
= − |
|
||||||
|
2 |
|
n2 |
f (ς) . |
||||||||||||
a |
|
|
|
|
|
|
|
|
n |
|
|
|||||
Отметим, что ошибка при вычислении интеграла по формуле трапе- ций убывает, по крайней мере, пропорционально квадрату длины наи- большего интервала разбиения.
Итак, абсолютная погрешность вычисления определенного интеграла по формуле трапеций не превосходит величины, которую можно оценить неравенством
(n) < sup |
|
f |
′′ |
(x) |
|
|
(b − a)3 |
|
|
||||||
|
|
|
12n2 |
||||
[ab] |
|
|
|
|
|
|
|
|
|
|
9.4. Формула Симпсона
Данный способ приближенного вычисления определенных интегра- лов основан на замене частичных дуг графика подынтегральной функции не фордами (отрезками), а дугами парабол и, следовательно, замене час-
тичных криволинейных трапеций параболическими. Интервал [a,b] точ-
ками a = x0 , x1, |
x2 ,..., x2n = b разбиваем на 2n равных частей длины |
||||||||||||||
|
h = |
b − a |
, x |
|
= a + |
b − a |
k, k = |
|
|
|
|
||||
|
k |
1,2n − 1. |
|||||||||||||
|
|
|
|||||||||||||
|
|
2n |
|
|
|
n |
|||||||||
|
|
|
|
|
|
||||||||||
Через каждые три точки |
|
M 0 |
, M1 и M 2 , M 2 , M3 и M 4 , … |
||||||||||||
M 2n − 2 , M 2n −1 и |
M 2n проведем параболы, уравнения которых имеют вид |
||||||||||||||
|
|
|
|
(x) = a x2 |
+ b x + c , k = |
|
. |
||||||||
|
|
y |
k |
1, n |
|||||||||||
|
|
|
|
|
k |
|
k |
|
k |
||||||
298
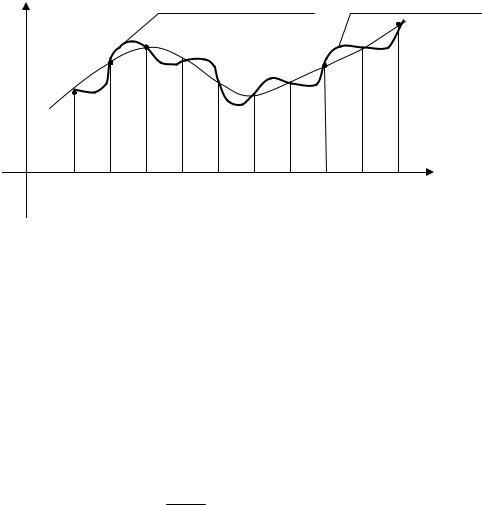
|
Заменяя площадь криволинейной трапеции, ограниченной графиком |
|||||||||||||||||
функции y = f(x) |
на |
[a,b] , |
суммой площадей фигур, лежащих под пара- |
|||||||||||||||
болами, получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
b |
f (x)dx ≈ x2 |
(a x2 |
+ b x + c )dx + x4 |
(a x2 |
+ b x + c )dx + ... + |
x2n |
(a |
n |
x2 + b x + c )dx (5) |
|||||||||
∫ |
∫ |
1 |
|
1 |
1 |
|
∫ |
2 |
2 |
|
2 |
|
|
∫ |
|
n |
n |
|
a |
x0 |
|
|
|
|
|
x2 |
|
|
|
|
|
x2n−2 |
|
|
|
|
|
|
y |
y = a x2 + b x |
+ c |
y = a |
n |
x2 + b |
x + c |
n |
|
|
|
|
||||||
|
|
|
1 |
1 |
|
1 |
|
1 |
|
n |
|
|
|
B = M 2n |
|
|||
|
|
|
|
|
|
M 2 |
|
|
|
|
|
|
|
|
|
|||
|
M 0 = A |
|
M1 |
|
|
|
|
|
M 2n −1 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
a = x0 x1 x2 |
x2n − 2 |
x2n |
х |
Так как
|
|
x2 |
|
|
|
|
|
|
a1 |
|
|
|
|
b1 |
|
|
|
|
|
|||
|
|
∫ (a1x2 + b1x + c1)dx |
= |
|
(x23 - x03 ) + |
(x22 - x02 ) + c1 (x2 - x0 ) = |
||||||||||||||||
|
|
|
|
|
||||||||||||||||||
|
|
x0 |
|
|
|
|
|
|
|
3 |
|
|
|
2 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
x2 - x0 |
× (2a (x2 |
+ x x + x2 ) + 3b (x + x ) + 6c = |
|
|||||||||||||||
|
|
|
|
|
||||||||||||||||||
|
|
|
6 |
|
1 |
2 |
2 |
0 |
0 |
|
|
1 |
2 |
0 |
1 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
b - a |
(a x2 |
|
|
|
|
x + x |
|
2 |
|
|
|
x + x |
|
+ a x2 |
|
||||||
= |
|
+ b x + c + 4a |
|
|
|
2 0 |
|
|
+ 4b |
|
2 |
0 |
+ 4c |
+ b x + c ) = |
||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
6n |
1 0 |
1 0 1 |
1 |
2 |
|
1 |
|
2 |
|
1 |
1 2 |
1 2 1 |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
= b - a ( y0 + 4 y1 + y2 ) 6n
Выполняя аналогично интегрирование в равенстве (5) и просумми- ровав, получим
b |
f (x)dx » |
b - a |
( y0 + y2n + 2( y2 + y4 + ... + y2n − 2 ) + 4( y1 + y3 + ... + y2n −1)) (6) |
|
∫ |
||||
|
||||
a |
|
6n |
||
|
|
|
||
Это формула Симпсона или формула парабол.
Оценка погрешности, получающаяся при вычислении интеграла по формуле Симпсона, может быть получена аналогично, как и для формулы
299

трапеций с учетом некоторых особенностей. Предполагается, что сущест-
вует и непрерывна функция f IV (x) на отрезке |
[a,b] . Рассмотрим вспо- |
||||||||||||||
могательные функции |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
c +t |
|
t |
[ f (c + t) + 4(c) + f (c - t)] |
|
|
||||||||
|
y(t) = ∫ |
f (x)dx - |
|
|
|||||||||||
|
|
|
|
||||||||||||
|
|
c −t |
3 |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
t5 |
|
|
|
|
|
|||
|
|
|
|
j(t) = y(t) - |
y(h), |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
h5 |
|
|
|
|
|
где ψ(h) |
– есть разность площадей рассматриваемых трапеций. |
|
|||||||||||||
Дифференцируя |
ϕ(t) трижды и применяя теорему о конечных при- |
||||||||||||||
ращениях, учитывая свойства функции |
ϕ(t) , получаем |
|
|
|
|||||||||||
|
|
|
|
y(h) = - |
h5 |
|
f IV (Vi ) |
|
|
|
|
||||
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
90 |
|
|
|
|
|
|
|
|||
x2k |
f (x)dx - |
(b - a) |
+ 4 y2k −1 + y2k ) = - |
(b - a)5 |
× f |
( IV ) |
(Vk ) . |
||||||||
∫ |
|
|
( y2k − 2 |
|
|
||||||||||
6n |
|
2880n5 |
|
||||||||||||
x2k −2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Суммируя последнее соотношение по k =1, n , получим (аналогично, как и для формулы трапеций), что оценка погрешности имеет вид
- (b - a)5 × f IV (V) , 2880n4
где ς (ab) .
Отметим, что ошибка при приближенном вычислении интеграла по формуле Симпсона убывает, по крайней мере, пропорционально четвертой степени длины наибольшего интервала разбиения отрезка [a,b].
Если же f(x) есть многочлен не выше третей степени, то f IV (x) = 0
и формула Симпсона является не приближенной, а точной.
Итак, абсолютная погрешность вычисления определенного интеграла по формуле Симпсона не превосходит
D(n) £ sup f IV (x) (b − a)5 . 2880n4
300
