Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Пензенский Государственный Университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

умк_Цывис_Функции_Интеграл. исчисл

..pdf

Скачиваний:

Добавлен:

18.05.2015

Размер:

4.7 Mб

Скачать

☆

<<< < Предыдущая 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 3132 / 3632 33 34 35 36 > Следующая >>>

	y
c	S(x)
	x = ψ1( y)

x = ψ2 ( y)

Таким образом, вычисление двойного интеграла по области дится к вычислению повторного интеграла по формулам

	b ϕ2 ( x)
∫∫	f (x, y)dxdy = ∫	∫

D	a ϕ1 ( x)
	d ψ2 ( y)
∫∫ f (x, y)dxdy = ∫		∫

D	c ψ1 ( y)

Обратите внимание (формула (9)):

f (x, y)dy dx ,

f (x, y)dx dy .

D сво-

(9)

(10)

1.Пределы внешнего интеграла по x в формуле (9) – это наимень- шее и наибольшее значения x во всей области D, т.е. крайние точки проекции области D на ось Ox;

2.Пределы внутреннего интеграла по y – это правые части уравне- ний линий входа и выхода, разрешенных относительно y;

3.Сначала вычисляется внутренний интеграл по y

ϕ2 ( x)

∫f (x, y)dy ,

ϕ1 ( x)

в котором x считается постоянным.

Обратите внимание (формула (10)):

1. Пределы внешнего интеграла по y в формуле (10) – это наименьшее и наибольшее значения y во всей области D, т.е. крайние точки проекции области D на ось Oy;

311

2.Пределы внутреннего интеграла по x – это правые части уравнений линий входа и выхода, разрешенных относительно x;

3.Сначала вычисляется внутренний интеграл по x

ψ2 ( y)

∫f (x, y)dx ,

ψ1 ( y)

в котором y считается постоянным.

Обратите внимание (формула (8)):

1.При переходе от двойного интеграла к повторным у внешнего инте- грала пределы интегрирования всегда постоянные числа;

2.Если внешний интеграл вычисляем по x, то у внутреннего интеграла пределы интегрирования зависят только от x (могут быть и постоян- ными числами);

3.Если внешний интеграл вычисляем по y, то у внешнего интеграла пределы интегрирования зависят только от y (могут быть и постоян- ными числами).

Замечание 2. Если область D не является правильной ни в направ- лении оси Ox, ни в направлении оси Oy, то для вычисления двойного ин- теграла по такой области требуется, прежде всего, разбить ее на правиль- ные области и интеграл по области D заменить суммой интегралов по со- ответствующим областям.

Изменение порядка интегрирования.

1. Пусть требуется изменить порядок интегрирования в повторном интеграле

	b ϕ2 ( x)
ID	= ∫	∫	f (x, y)dy dx .

	a ϕ1 ( x)

Для решения данной задачи сначала восстановим область интегриро- вания D по известным пределам данного повторного интеграла.

Имеем D: x = a, x = b, y = ϕ1 (x) , y = ϕ2 (x) .

Построим графики этих функций (линий) и определим область D. Спроектируем область D на ось Oy, найдем уравнения прямых y = c и y = d, ограничивающих снизу и сверху полосу, в которой расположена об- ласть D. Затем проводим лучи, параллельные оси Ox и одинаково с ней направленные, и находим левую границу области D: x = ψ1 ( y) и правую – x = ψ2 ( y) . Если какая-либо из этих границ области D состоит из двух или большего числа линий, заданных различными уравнениями, то область D

312

разбиваем на части, а интеграл – на сумму интегралов по этим частям. За- тем применяем формулу

	b ϕ2 ( x)			d ψ2 ( y)
ID	= ∫	∫	f (x, y)dy dx = ∫		∫	f (x, y)dx dy .

	a ϕ1 ( x)			c ψ1 ( y)

2. Пусть требуется изменить порядок интегрирования в повторном интеграле

	d ψ2 ( y)
ID	= ∫	∫ f (x, y)dx dy .

	c ψ1 ( y)
Записав уравнения границ		области	D: y = c, y = d,	x = ψ1 ( y) ,
x = ψ2 ( y) , строим эту область. Спроектировав эту область D				на ось Ox,

находим уравнения прямых x = a и x = b, ограничивающих слева и спра- ва полосу, в которой расположена область D. Проводим лучи, параллель- ные оси Oy и одинаково с ней направленные, тем самым устанавливаем линии входа и выхода для области D: y = ϕ1 (x) и y = ϕ2 (x) . Затем приме-

няем формулу

d ψ2 ( y)

ID = ∫ ∫

c ψ1 ( y)

	b ϕ2 ( x)
f (x, y)dx dy = ∫		∫

	a ϕ1 ( x)

f (x, y)dy dx .

Пример 1. В двойном интеграле ∫∫ f (x, y)dxdy расставить пределы

интегрирования (двумя способами) по области D: y = 0, y = x, y + x = 2. Решение. Запишем уравнения границ области D и построим данную об- ласть на плоскости

y = x

1 B

			C
0	1	2	x
			x + y = 2

313

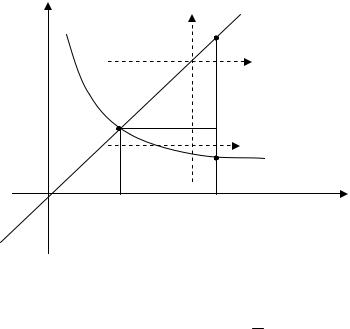
Тогда имеем

	1 2 − y						1	2 − y
∫∫ f (x, y)dxdy = ∫		∫	f (x, y)dx dy				= ∫dy ∫ f (x, y)dx

D	0	y					0	y
	1	x		2			2 − x
∫∫ f (x, y)dxdy = ∫dx∫ f (x, y)dy + ∫dx ∫								f (x, y)dy
D	0	0		1			0
Пример 2. В двойном интеграле ∫∫				x	2	dxdy		расставить пределы ин-

					2
			D y		2
тегрирования (двумя способами) по области							D: y = x, xy = 1, x = 2 и вы-
числить данный интеграл.
Решение. Строим область D на плоскости
y
							y = x
							B1
			D1
		A					B2
			D2
							B	y =	1
							B	y =	x
									x
		1			2					x

Тогда имеем координаты точек пересечения:

A(1;1), B2 (1;2), B1 (2;2), B(2; 1 ) . 2

Перейдем от двойного интеграла к повторному, выбирая внешний интеграл по x (т.е. x меняется в постоянных пределах), а внутренний – по y, т.е. переходим к интегралу вида

∫dx∫	x2
			dy .
	y	2

Для определения пределов интегрирования (внешний интеграл) по x (постоянные пределы интегрирования) спроектируем область D на ось Ox. В результате получим, что x [1;2], т.е. x = 1 и x = 2.

Для определения пределов интегрирования по y проведем лучи, па- раллельные оси Oy и одинаково с ней направленные. Эти лучи будут вхо-

314

дить в область

D на дуге АВ (уравнение

y =

)

и выходить на отрезке

AB (уравнение

y = x), т.е. нижний предел

y =

, верхний предел – y = x

при интегрировании по y.

Тогда получим

2 x

∫∫

dxdy = ∫dx ∫

dy = ∫

∫

dy dx .

y 2

Перейдем от двойного интеграла к повторному в другом порядке, взяв внешний интеграл по y, а внутренний – по x. Для определения преде- лов интегрирования по x, проведем лучи, параллельные оси Ox и одина- ково с ней направленные. Линией выхода таких лучей является отрезок

BB1 на прямой	x = 2, а линией входа является кривая			BAB1 , которая со-
стоит из линий	ВА (уравнение x =	1	) и AB (уравнение	x = y), имеющих

		y	1

разные уравнения. Поэтому область D разбиваем на две области D1 и D2

прямой, параллельной оси Ox и проходящей через точку А (где меняется уравнение кривой BAB1 ), а исходный интеграл – на сумму двух интегралов:

∫∫	x2	dxdy = ∫∫	x2	dxdy +	∫∫		x2	dxdy .
			y 2
D y 2		D			D	2	y 2
		1

Для первого интеграла линией входа в направлении оси Ox является

дуга АВ гиперболы (уравнение x = 1 ), а линией выхода является отрезок y

BB2 прямой x = 2. Верхним пределом интегрирования по x будет x = 2, а

нижний – x = 1 . Чтобы найти пределы интегрирования для внешнего ин- y

теграла по y, спроектируем область

, т.е. нижний предел по y

будет

Следовательно, имеем

∫∫

dxdy =

∫dy ∫

y 2

D1 на ось Oy и получим отрезок

1 , верхний 1.


1		2	x	2
dx = ∫		∫	x		dx dy .
dx = ∫		∫	y 2		dx dy .
1		1	y 2


2	y

315

Поступая аналогично, для второго интеграла по области D2 получим

	x	2	2	2	x	2
∫∫	x		dxdy = ∫dy ∫		x		dx .
∫∫	y 2		dxdy = ∫dy ∫		y 2		dx .
D2	y 2		1	1	y 2

Тогда исходный интеграл имеет вид

	x	2	1		2		x	2	2	2	x	2
∫∫			dxdy = ∫dy ∫						dx + ∫dy ∫				dx .
	y 2						y 2
D				1		1			1	y y 2
			2			y

Для вычисления интеграла выбираем порядок интегрирования, при котором нет надобности разбивать область интегрирования на части, т.е. воспользуемся формулой

I D = ∫∫ f (x, y)dxdy = ∫dx ∫

dy .

Вычисление интеграла I D

начинаем с нахождения внутреннего ин-

теграла, где интегрирование ведется по y, а x считаем постоянной.

ID = ∫ x2dx ∫ dy = ∫ x2

− 1

dx = ∫ x2

− 1

+ x dx =∫(x3

− x)dx = 9 .

1 y2

Пример 3. Изменить порядок интегрирования в повторном интеграле

I D =

9 + y 2

∫dy ∫ f (x, y)dx .

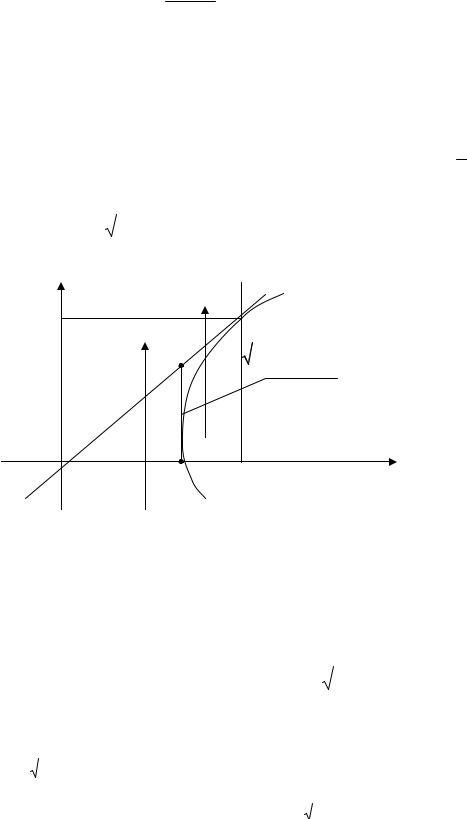
Решение. Запишем уравнения границ области интегрирования: y = 0,

y = 4, x = 5 y, x = 9 + y2 и построим эти линии. Уравнение x = 9 + y 2

определяет гиперболу, т.к. при возведении в квадрат обоих частей уравне-

ния получим x2 = 9 + y 2 или x2 − y 2 = 9 – это уравнение гиперболы. Но

так как x = +9 + y 2 , то выбираем только правую ветвь этой гиперболы.

316

	x =	5	y
				найдем координаты точки А(5;4).
Решая систему уравнений	4

x = 9 + y 2

Таким образом, наименьшее значение x для рассматриваемой об- ласти равно 0, наибольшее – x = 5.

Установим нижнюю и верхнюю границы области D. Для этого про- ведем лучи, параллельные оси Oy и одинаково с ней направленные. Линия

выхода таких лучей состоит из отрезка ОА прямой (уравнение y = 4 x ), а

					5
линия входа состоит из отрезка ОВ оси					Ox (уравнение y = 0) и дуги ВА ги-
перболы (уравнение y =				.
перболы (уравнение y =			x2 − 9	.
y
4					A

			D		y = x2 − 9
2
y =	4	x
y =		x
5
			D1 B			x
3					5

Поэтому область D разобьем прямой, параллельной оси Oy и прохо- дящей через точку B, на две области и расставим пределы интегрирования по каждой из областей. Для этого определим уравнения линий входа и вы-

хода, запишем выражение y через x: y =							4		y = +						(взят знак «+»,
							4	x ;					x2 − 9
								x ;					x2 − 9
					5
потому что рассматривается верхняя ветвь гиперболы														y ³ 0 ). Тогда имеем
					4	x				4		x
4	9 + y 2			3					5
4	9 + y 2			3	5				5		5
∫dy ∫ f (x, y)dx = ∫dx ∫ f (x, y)dy + ∫dx ∫ f (x, y)dy .
0		5		0	0				3
0		5	y	0	0				3	x 2 −9
	4		y							x 2 −9
	4

317

Пример 4. В двойном интеграле расставить пределы интегрирования в том и другом порядке по области D и вычислить данный интеграл:

4.1. ∫∫e x dxdy	D : y =1, y = 2,		y = e x , y = x ;
D
4.2. ∫∫ x3dxdy	D : x = 0, y = x,		y = 2 - x2 (x ³ 0) ;
D
4.3. ∫∫(x2 + 2xy)dxdy		D : y = 0,	y =1, y = x, y = x -1.
D

Решение.

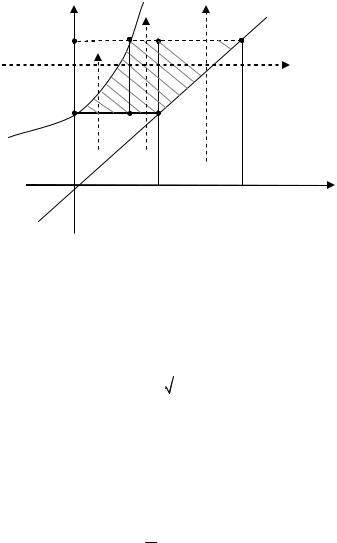
4.1. Построим область интегрирования и расставим пределы интег- рирования.

2 y = ex

E N C

A M B

y = x

1 2

Тогда имеем

	ln 2	ex	1	2	2	2	2	y	ex dx = e2 - e -			3
∫∫ex dxdy = ∫		dx ∫ ex dy + ∫ dx∫ex dy + ∫dx∫ex dy = ∫dy ∫										3	.
∫∫ex dxdy = ∫		dx ∫ ex dy + ∫ dx∫ex dy + ∫dx∫ex dy = ∫dy ∫											.
D	0	1	ln 2	1	1	x	1	ln y	2
D	0	1	ln 2	1	1	x	1	ln y
							2 − x2
		1	y	2	2 − y	1	2 − x2			2
	4.2. ∫∫ x3dxdy = ∫dy ∫ x3dx + ∫dy				∫	x3dx = ∫dx	∫	x3dy =		2	;
	4.2. ∫∫ x3dxdy = ∫dy ∫ x3dx + ∫dy				∫	x3dx = ∫dx	∫	x3dy =			;
	D	0	0	1	0	0	x		15
	D	0	0	1	0	0	x
			1	x		2	1
	4.3. ∫∫(x2 + 2xy)dxdy = ∫dx∫(x2 + 2xy)dy + ∫dx ∫							(x2 + 2xy)dy =
	D		0	0		1	x −1

1 y +1

=∫dy ∫ (x2 + 2xy)dx = 7 .

0	y	3

318

	2	2 − x
3
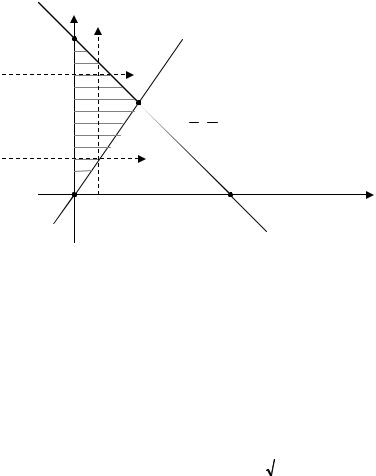
Пример 5. В повторном интеграле ID = ∫ dx			∫ f (x, y)dy поменять
0			2 x
порядок интегрирования.
Решение. Для решения данной задачи требуется:
а) восстановить область интегрирования		D,	исходя из границ по-
вторного интеграла ID ;

б) записать ID с постоянными пределами по y и переменными по x.

Границы области D: x = 0, x =	2	, y = 2x, y = 2 − x .

3
Строим область интегрирования
y

y = 2x

2 4;3 3

y = 2 – x

Тогда имеем

	2	2 − x	4		y			2 − y
3			3	2		2
ID = ∫ dx ∫ f (x, y)dy = ∫ dy ∫ f (x, y)dx + ∫ dy ∫ f (x, y)dx .
0		2 x	0	0			4	0
						3

Пример 6. Поменять порядок интегрирования.

2		2 − x
6.1. ∫ dx			∫		f (x, y)dy ;
−6		x	2	−1

	4
	4
1	π−arcsin y
6.3. ∫dy				∫	f (x, y)dx .
0		arcsin y

9				3			3
		y
16			f (x, y)dx +	4			4
6.2. ∫ dy ∫						∫ dy ∫ f (x, y)dx ;
0	y				9			y
				16

319

y +1

2 − y

Решение.

6.1.

∫ dy

∫ f (x, y)dx + ∫dy

∫ f (x, y)dx ;

−1

−2

y +1

π sin x

6.2. ∫dx ∫

f (x, y)dy ;

6.3. ∫dx

∫

f (x, y)dy .

Пример 7. Расставить пределы интегрирования в том и другом по-

рядке в двойном интеграле

∫∫ f (x, y)dxdy

для указанных областей D.

7.1.D – прямоугольник с вершинами О(0;0), А(2;0), В(2;1), С(0;1);

7.2.D – прямоугольник с вершинами О(0;0), А(1;0), В(1;1);

7.3.D – трапеция с вершинами О(0;0), А(2;0), В(1;1), С(0;1);

7.4.D – параллелограмм с вершинами А(1;1), В(2;4), С(2;7), D(1;5).

Решение.

1	2	2	1	1	1	1	x
7.1. ∫dy∫ f (x, y)dx = ∫dx∫ f (x, y)dy ; 7.2.				∫dy∫ f (x, y)dx = ∫dx∫ f (x, y)dy ;
0	0	0	0	0	y	0	0

1	2 − y	1	1		2 2 − x
7.3. ∫dy	∫ f (x, y)dx = ∫dx∫ f (x, y)dy + ∫dx					∫ f (x, y)dy ;
0	0	0	0		1	0
	2 x +3			y + 2
2		4			5	2	7	2
2		4	3		5	2	7	2
7.4. ∫dx	∫	f (x, y)dy = ∫dy ∫			f (x, y)dx + ∫dy∫ f (x, y)dx + ∫dy			∫ f (x, y)dx .
1	3x − 2	1	1		4	1	5	y −3
								2
		§ 4. Замена переменных в двойном интеграле
Пусть в плоскости				Ox	задана область		D, ограниченная линией L.

Пусть координаты x и y являются функциями новых переменных u и v

	x = ϕ(u,v)	y = ψ(u,v)	(1)
при этом считаем, что функции ϕ(u,v)		и ψ(u,v) однозначны, непрерывны
и имеют непрерывные производные в некоторой области D1 . Тогда фор-
мула (1)	устанавливает взаимнооднозначное соответствие между точками
(x, y) D	и (u,v) D1 . Это означает, что каждой точке P(x, y)		на плоско-
сти Oxy однозначно соответствует точка P(u,v) на плоскости			Ouv с ко-
ординатами u и v, которые определяются по формуле (1).

320

<<< < Предыдущая 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 3132 / 3632 33 34 35 36 > Следующая >>>

Соседние файлы в папке Высшая математика (РТФ)

#
18.05.20154.76 Mб34умк_Вакульчик_Элементы векторной алгебры.pdf
#
18.05.20155.38 Mб39умк_Вакульчик_Элементы линейной алгебры.pdf
#
18.05.20151.33 Mб42умк_Мальцев_Осн дискретной матем.pdf
#
18.05.20153.75 Mб40умк_Пальчик_Теория вероятностей.pdf
#
18.05.20155.68 Mб33умк_Цывис_Диф.уравнения_Ряды.pdf
#
18.05.20154.7 Mб40умк_Цывис_Функции_Интеграл. исчисл..pdf
#
18.05.20153.54 Mб77умк_Яско_ Диф.уравнения_Ряды.pdf