умк_Цывис_Функции_Интеграл. исчисл

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Пензенский Государственный Университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

= 2 | cos t |= cos 2t ,

dx = 2sin tdt ,

= 2 | cos t |= cos 2t ,

т.к. cos t > 0

для x [− π , π] .

..pdf

Скачиваний:

Добавлен:

18.05.2015

Размер:

4.7 Mб

Скачать

☆

<<< < Предыдущая 9 10 11 12 13 14 15 16 17 18 19 2021 / 3621 22 23 24 25 26 27 28 29 30 31 32 33 > Следующая >>>

x = x

− x = qi+1 − qi = qi (q −1)

i+1

max x = qi

(q −1) → 0 при n → ∞ , т.е. при q → 1.

Точки εi

выбирают

так:

правые

концы

отрезков

[xi,xi+1], т.е.

= x

= qi+1 .

i+1

Тогда интегральная сумма имеет вид

n−1

−1)

h(2n

Sn = ∑

x =

∑

qi (q −1) =

(q −1)

i=0

ξi

i=0 qi+1

Тогда I = lim Sn

n →∞

правило Лопиталя,

I = ∫ dx = ln 2 .

1 x


= lim	n[2	n	− 1]	= ln 2 так как	используя, например,
			1
n →∞

	2n
или	то, что 2x −1 ≈ x ln 2				при x → 0 . Тогда

4.2. Вычисление определенных интегралов, опираясь на их геометрический смысл

Данный метод вычисления определенных интегралов основан на том, что определенный интеграл от непрерывной функции на отрезке [a,b] чис- ленно равен площади криволинейной трапеции с основанием [a,b] ограни- ченной сверху функцией y = f(x) и прямыми x = a, x = b.

Пример 4. Найти величину интеграла I = ∫ 16 − x2 dx .

Решение. Уравнение y = 16 − x2 определяет верхнюю половину окруж-

ности x2 + y2 = 16. Та часть линии, которая получается при x [0, 4], лежит в первой координатной четверти. Отсюда заключаем, что криволинейная трапеция, ограниченная линиями х = 0, х = 4, у = 0, y = 16 − x2 есть чет-

верть круга x2 + y2 = 16; ее площадь равна 4 π .

Следовательно I = ∫ 16 − x2 dx = 4π .

Пример 5. Вычислить интеграл I = ∫ 1 − x dx .

201

1 A

Решение. На отрезке [0,2] построим график функции y = 1 - x .

Величина искомого интеграла I – это площадь треугольников DАОС и DCBD.

D x

Так

как

S AOC = S CDB =

то

I = 2S AOC = 1.

Пример 6. Вычислить интеграл

I = ∫

dx .

Решение. 1) Если 0 < a < b, тогда искомый интеграл – это площадь прямо-

угольника с основанием длины (b –

a) и высотой 1 –

I =1× (b - a) = b - a ;

2) если a < b < 0 тогда искомый интеграл –

это площадь прямоуголь-

ника с основанием длинны (a – b) и высотой 1 –

I =1× (a - b) ;

3) если a < 0 < b, то в этом случае искомый интеграл – это площадь

прямоугольников

высотой

(– а)

основанием

–

I =1× (-a) +1×b =1× (-a + b) .

Рассмотренные случаи можно записать в виде одной формулы

I = ∫

dx =1

× (

)

Пример 7. Опираясь на геометрический смысл определенного инте-

грала доказать, что

2π

1. ∫ sin5 xdx = 0 ;

∫ e− x2dx = 2∫e− x2 dx .

−1

Приведем решение задачи 1. Докажем, что площадь, ограниченная

кривой y = sin5 x

на отрезке [0, p] , лежащая над осью Ox равна площади

ограниченной кривой

y = sin5 x на отрезке

[p, 2p] , лежащей над осью Ox.

Действительно,

если

p < x £ 2p,

тогда

x = x1 + π, 0 < x1 < π

sin5 x = sin5 (p + x ) = -sin5 x .

x Î[p, 2p] ,

Значит, вторая половина графика

которую получают из

первой половины

x Î[0, p]

сдвигом вправо на

π и симметрично относи-

тельно оси Ox.

2π

Значит ∫ sin5 xdx = 0 .

202

График функции y = sin5 x на отрезе [0,2π] имеет следующий вид

S1		2π	x
0	π	S2

4.3.

Вычисление интегралов

по формуле Ньютона-Лейбница

Пример 8. Вычислить интеграл

I = ∫

1 + x2

Решение.

Одной из первообразных для функции f (x) =

является

1 + x2

функция

F (x) = arctgx , тогда применяя формулу Ньютона-Лейбница, по-

= arctgx|1

= p - 0 = p .

лучим I = ∫

1 + x2

x2 ,0 £ x £1

Пример 9. Вычислить интеграл

I = ∫

f (x)dx, f (x) =

x,1 < x £ 4

Решение. Используя свойство определенного интеграла, имеем

		4		1					4			x3		1		3	4
																3	4
															x 2
I = ∫ f (x)dx = ∫ x2dx + ∫ xdx =														+ 2			=
I = ∫ f (x)dx = ∫ x2dx + ∫ xdx =											3			+ 2	3		=
		0		0					1		3			0	3
		0		0					1					0			1
	1		2	3			1		2		1


=		+						+		(8 -1) =			(1 + 16 - 2) = 5
				(4	2	-1) =
				(4	2	-1) =			3
3		3					3		3		3

Пример 10. Вычислить интеграл I = ∫ dx .

1 x4

Решение. По формуле Ньютона-Лейбница имеем

2 dx		2	−4		1		−3	2		1		1	2		1	1

I = ∫		= ∫ x		dx = -		x			= -		×			= -			-1	=
	4											x3
1 x		1			3			1		3			1		3	8

7 .

203

7	dx
Пример 11. Вычислить интеграл I = ∫	dx	по формуле Ньюто-
Пример 11. Вычислить интеграл I = ∫	(x - 4)2	по формуле Ньюто-
0	(x - 4)2
на-Лейбница.

Решение. Вычислить данный интеграл, используя формулу Ньютона- Лейбница, нельзя. Если применить формулу Ньютона-Лейбница формаль- но, то получим неверный результат. Действительно,

7				7

	dx		1			1		1			1
I = ∫		= -			= -		+		= -			.
	(x - 4)2		(x - 4)
0				0	3 4					12
					f (x) =					1			> 0 ,
Отметим, что подынтегральная функция														и следова-

										(x - 4)2

тельно согласно свойствам определенного интеграла I не может равняться отрицательному числу. Дело в том, что подынтегральная функция

f (x) =

в точке

x = 4 имеет разрыв второго рода (бесконечный) в

(x - 4)2

точке

x = 4, принадлежащий отрезку интегрирования. Значит, применять

формулу Ньютона-Лейбница нельзя.

Пример 12. Доказать, что для любых

m N

и n N

справедливы

равенства:

1. I = ∫ sin mx × cos nxdx = 0 ;

2. I = ∫ sin mx ×sin nxdx = 0 , m ¹ n ;

−π

3. I = ∫ cos mx × cos nxdx = 0 , m ¹ n ;

4. I = ∫ sin2 mxdx = ∫ cos2 nxdx .

−π

Решение.

1. Так как 2sin a × cosb = sin(a + b) + sin(a - b) , тогда

I = ∫ sin mx × cos nxdx =

∫ sin(m + n)xdx +

∫ sin(m - n)xdx .

−π

Если m ¹ n , тогда I =

cos(m + n)x

cos(m - n)x

= 0 ,

2(m + n)

−π 2(m - n)

−π

так как cos pk = (-1)k

для любого k Z .

n N . Следовательно,

Если m = n, то I =

∫ sin 2nxdx = 0

для любого

−π

I = 0 для любых m, n N .

204

2. Так как	1− cos 2α = 2sin2 α; 1+ cos 2α = 2cos2 α и учитывая, что
π	π

∫ cos 2nxdx = 0 при любом n N , а	∫ dx = 2π , получим искомое равенство.
−π	−π

Равенства 3 и 4 в примере 12 решаются аналогично.

Замечание 1. При вычислении определенных интегралов с помощью формулы Ньютона-Лейбница, следует проверять условия законности его применения. Формула Ньютона-Лейбница применяется для вычисления определенного интеграла от непрерывности на [ab] функции f(x) тогда и только тогда, когда равенство F '(x )= f (x ) выполняется для любого x [ab] . (F(x) – первообразная для f(x) на [ab]). В частности, F(x) первооб- разная должна быть непрерывной функцией на всем отрезке [ab]. Так как при нарушении законности применения формулы Ньютона-Лейбница, при- ходим к неверному результату.

3	dx
Пример 13. Вычислить интеграл I = ∫		.
	1 + x2
0
Решение. 1. Так как одна из первообразных для функции f (x) =			1	не-
			+ x2
		1

прерывной на [0; 3] является функция F(x) = arctg x непрерывна на [0; π] 3

и равенство F '(x )= f (x ) выполняется на всем этом отрезке, то формула Ньютона-Лейбница применима, и получим искомый интеграл

− arctg0 = π .

I =

= arctgx 3

= arctg

∫

1 + x

2. Рассмотрим другой способ вычисления исходного интеграла

3) − arctg0] = − π ,

| 3

I = ∫

arctg

[arctg(−

1 + x2

1 − x2

, x ¹ ±1.

где

(

arctg

)' =

1 − x2

1 + x2

Результат неверный, т.к. интеграл отовсюду положительной, непрерыв-

ной функции на [0; 3] оказался отрицательным. Ошибка связана с тем, что

в точке x = 1 [0;

функция

arctg

3] терпит разрыв первого рода:

1 − x2

lim

arctg

= π ;

lim

arctg

= − π .

1 − x2

х→1− 0

х→1+ 0

205

Правильный результат можно найти и при помощи функции

F (x) =	1	arctg	2x	.
			1 − x2
2

Для этого отрезок интегрирования [0; 3] следует разбить на два отрез-

ка [0;1] и [1; 3], и учесть предельные значения функции F(x) при x → 1 0 . В этом случае на каждом из отрезков первообразная – непрерывная функ- ция, а, следовательно, законно применение формулы Ньютона-Лейбница

	3	dx		1		dx			3	dx		1		2x				1		2x
I =			=					+			= (					1	+ (					3	=
	∫			∫					∫				arctg		)				arctg		)

		1 + x2			1	+ x	2			1 + x2	2			1 − x2	\|		2			1 − x2	\|
	0			0					1							0						1

= ( π − 0) + (− π − (− π)) = π − π = π .

4	6	4	2	6	3
		π
		π	1 + cos 2x
Пример 14. Вычислить интеграл		I = ∫				dx .
Пример 14. Вычислить интеграл		I = ∫		2		dx .
		0		2
		0

Решение. Так как 1 + cos 2x

		cos x,0 ≤ x ≤ π
		cos x,0 ≤ x ≤ π
=				2
=	cos2 x =\| cos x \|=		π	2
		− cos x,	π	≤ x ≤ π
			2

Следовательно,

π			π	π	π
	1 + cos 2x	2			π	π
	1 + cos 2x	2				π
I = ∫			= ∫ cos xdx + ∫ cos xdx = sin x\|02			− sin x\|π = (1	− 0)	− (−1 − 0)	= 2.
I = ∫	2		= ∫ cos xdx + ∫ cos xdx = sin x\|02			− sin x\|π = (1	− 0)	− (−1 − 0)	= 2.
0	2	0		π		2
				2		2
				2

Замечание 2. Если не обратить внимание на то, что cos x отрицате-

лен на отрезке [ π ;π ], то получим заведомо неверный результат т.к. 2

I = ∫cos xdx = 0.

100π

I = ∫

= 0.

Пример 15. Вычислить интеграл

1 − cos 2x

Решение. 1)Так как имеет место

1 − cos 2x

2 | sin x | . Поэтому

100π

2π

3π

I = ∫

1 − cos 2xdx = ∫

| sin x | dx =

2(∫sin xdx − ∫ sin xdx + ∫ sin xdx −

2π

4π

100π

− ∫ sin xdx + ... +

∫ sin xdx) =

2(2 + 2 + ... + 2) = 200

3π

99π

206

2) Предложим второй способ решения данной задачи.

| sin x | и

Так

как имеет место равенство

1 - cos 2x

так как

| sin x | имеет период равный π , то

100π

∫

1 - cos 2xdx = 2 ∫ | sin x | dx =100 × 2 ∫ sin xdx = 200

2 .

§5. Замена переменной в определенном интеграле

Теорема 1. Пусть функция f(x) непрерывна на интервале ( a0 ;b0 ), а

функция ϕ(x) имеет непрерывную производную на интервале (α0 ;β0 ) причем ϕ(t) (a0 ,b0 ) при всех t (α0 ,β0 ) . Тогда если α (α0 ,β0 ) , β (α0 ,β0 ) , a = ϕ(α) , b = ϕ(β) , то справедлива формула замены перемен-

ной в определенном интеграле

b	β
∫ f (x)dx = ∫ f (j(t))j'(t )dt .		(1)
a	α
Доказательство. Так как	a (a0 ,b0 ) и b (a0 ,b0 ) ,	а функция f(x) непре-

рывна на (a0 ,b0 ) , то в силу формулы Ньютона-Лейбница имеем

∫ f (x)dx = F (b) - F (a) ,

где F’(x)=f(x) для всех x (a0 ,b0 )

Функция F (ϕ(t)) является первообразной для функции, стоящей над знаком интеграла в правой части равенства (1), так как

d F (j(t)) = F '(j (t ))× j '(t )= f (j (t ))× j '(t . at

Применим формулу Ньютона-Лейбница к функции учетом j(a) = a,j(b) = b получим

(2)

f (j(t)) × j'(t ) с

β
∫ f (j(t)) × j'(t )dt = F (j (b ))- F (j (a ))= F (b )- F (a ).	(3)
α

Из равенств (2) и (3) следует формула (1).

Замечание 1. Одна из важных особенностей формулы (1) состоит в следующем: при вычислении неопределенного интеграла с помощью заме- ны переменной, получив искомую функцию, выраженную через новую пе-

207

ременную t, мы должны были возвращаться к старой переменной x, в оп- ределенном интеграле нет надобности. Если вычислен второй из опреде- ленных интегралов в равенстве (1), который представляет собой число, то тем самым вычислен и первый.

Пример 1. Пусть функция f(x) непрерывна на [−a, a]. Доказать что:

				a
1.1)	если f(x) –	нечетная функция, то		∫ f (x)dx = 0 ;
				−a
			a		a
1.2)	если f(x) –	четная функция, то ∫		f (x)dx =2∫ f (x)dx .
			−a		0
Решение: 1.1)		если	f(x) нечетная функция,		т.е. f(– x) = – f(x) для	всех
x [−a, a] , то, полагая x = – t и используя формулу (1) получаем
		0	0	a	a
		∫ f (x)dx = −∫ f (−t)dt = ∫(− f (t))dt = −∫ f (x)dx ,
	−a		a	0	0
		a	0	a
откуда следует, что ∫			f (x)dx = ∫ f (x)dx + ∫(x)dx = 0 ;
		−a	−a	0
				0	a
	1.2) если f(x) четная функция, то			∫ f (x)dx =∫ f (x)dx .
				−a	0
				a	a
Откуда следует, что имеет место равенство ∫					f (x)dx =2∫ f (x)dx .
				−a	0
	Пример 2. Доказать, что если f(x) непрерывна на R и периодическая
с периодом Т функция, то для любого a R справедливо равенство
			a +T	T
			∫ f (x)dx =∫ f (x)dx .			(4)
			a	0
Решение. В силу свойств определенного интеграла имеем
		a +T	0	T	a+T
		∫ f (x)dx =∫ f (x)dx + ∫ f (x)dx + ∫ f (x)dx .				(5)
		a	a	0	T

Полагая x = t + T и учитывая, что функция f(x) определена на R и f(t + T) = f(t) для всех t R в силу периодичности функции f(x), получаем

a +T	a	a	0
∫	f (x)dx = ∫ f (t + T )dt = ∫ f (t)dt = −∫ f (x)dx .			(6)
T	0	0	a

208

Из равенств (5) и (6) следует формула (4)

2.5π

Пример 3. Вычислить интеграл I = ∫ sin7 x × cos10 xdx .

− π

Решение. Подынтегральная функция периодическая с периодом 2π и не-

четная, поэтому

I = ∫ sin7 x × cos10 xdx = 0 .

			−π
Пример 4. Вычислить интеграл:
π		x sin x		1 ln(1 + x)
4.1. I = ∫			dx	4.2. I = ∫		dx
4.1. I = ∫			dx	4.2. I = ∫	1 + x2	dx
0	1	+ cos2 x		0	1 + x2

Решение:

4.1. I = ∫ x sin x 0 1 + cos2 x

π		π
2	x sin x		x sin x
dx = ∫		dx + ∫		dx ;
	1 + cos2 x		1 + cos2 x
0		π

x = p - t

(p - t)sin t

x sin x

∫

dx =

t Î[ ,0]

= -∫

π 1 + cos2 x

1 + cos2 t

dx = -dt

(p - t)sin t

sin t

t sin t

∫

dt = p∫

dt - ∫

dt.

1 + cos2 t

+ cos2 t

0 1

Тогда

x sin x

sin t

t sin t

I = ∫

dx =

∫

dx + p∫

dt - ∫

dt =

+ cos2

0 1

+ cos2 x

0 1

+ cos2 t

0 1

+ cos2 t

sin t

dt = -p(arctg(cos p)

- arctg(cos 0)) = p

= p∫

+ cos2 t

Замечание. Неопределенный интеграл

I = ∫

x sin x

не выража-

1 + cos2

ется в элементарных функциях. Но данный определенный интеграл, как показано выше, вычисляется, если использовать прием, связанный со свой- ствами функции и области интегрирования.

209

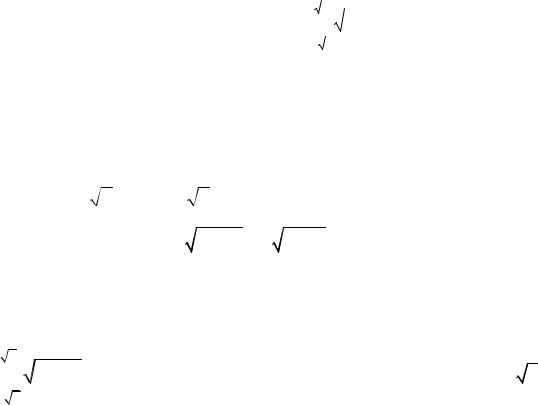
4.2. Ответ I = π ln 2 . Применяя подстановку x = tgt , получим

	π		π
	4		4	π + I1 − I
I = π ln 2 + ∫ ln sin(t +		π) − ∫ ln costdt =		π + I1 − I	2 ,
8	0	4	0	2
	0		0

затем доказываем, что I1 = I2, применяя к интегралу I2 подстановку t = π − U . 4

Данный пример по содержанию аналогичен 4.1, т.к. неопределенный

интеграл I = ∫	ln(1 + x)	dx не выражается в элементарных функциях, а соот-
интеграл I = ∫		dx не выражается в элементарных функциях, а соот-
	1 + x2
ветствующий определенный интеграл вычисляется.

Пример 5. Вычислить интеграл I =			2
			2
			∫ 4 − x	2 dx .
		−
		−	2

Решение. Пусть x = 2sin t , − π	≤ t ≤ + π . Функция x = ϕ(t) = sin 2t на отрез-
4	4

ке [− π , π] удовлетворяет условиям теоремы о замене переменной в опре- 4 4

деленном интеграле, так как она непрерывна, дифференцируема, монотон-

на и ϕ(− π) = −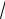2 , ϕ( π) = 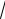2 .

Тогда

I = ∫

−2

4 − x2 dx = 4 ∫

− π

cos2 tdt = 2 ∫

− π

Пример 6. Вычислить интеграл:

π			π
3	dx		4	dx
6.1. I1 = ∫		;	6.2. I2 = ∫			;
	2 + cos x			4cos2 x +
0			0		9sin2 x

210

<<< < Предыдущая 9 10 11 12 13 14 15 16 17 18 19 2021 / 3621 22 23 24 25 26 27 28 29 30 31 32 33 > Следующая >>>

Соседние файлы в папке Высшая математика (РТФ)

#
18.05.20154.76 Mб33умк_Вакульчик_Элементы векторной алгебры.pdf
#
18.05.20155.38 Mб38умк_Вакульчик_Элементы линейной алгебры.pdf
#
18.05.20151.33 Mб40умк_Мальцев_Осн дискретной матем.pdf
#
18.05.20153.75 Mб39умк_Пальчик_Теория вероятностей.pdf
#
18.05.20155.68 Mб32умк_Цывис_Диф.уравнения_Ряды.pdf
#
18.05.20154.7 Mб39умк_Цывис_Функции_Интеграл. исчисл..pdf
#
18.05.20153.54 Mб76умк_Яско_ Диф.уравнения_Ряды.pdf