Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Пензенский Государственный Университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

умк_Цывис_Функции_Интеграл. исчисл

..pdf

Скачиваний:

Добавлен:

18.05.2015

Размер:

4.7 Mб

Скачать

☆

1 / 361 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

Министерство образования Республики Беларусь

Учреждение образования «Полоцкий государственный университет»

ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ

ИНТЕГРАЛЬНЫЕ ИСЧИСЛЕНИЯ

УЧЕБНО-МЕТОДИЧЕСКИЙ КОМПЛЕКС

для студентов технических специальностей

Составление и общая редакция Н. В. Цывиса

Новополоцк 2006

УДК 517(075.8) ББК 22.161я73

Ф 94

РЕЦЕНЗЕНТЫ:

К. О. Ананченко, доктор пед. наук, профессор УО «ВГТУ»; И. Б. Сороговец, канд. физ.-мат. наук, доцент

Рекомендован к изданию учебно-методической комиссией радиотехнического факультета

Ф 94 Функции нескольких переменных. Интегральные исчисления : учеб.-

метод. комплекс для студ. техн. спец. / сост. и общ. ред. Н. В. Цывиса. – Ново-

полоцк : ПГУ, 2006. – 356 с. ISBN 985-418-484-6

Рассмотрены функции нескольких переменных, неопределенный интеграл, оп- ределенный интеграл, двойной и тройной интегралы. Приведены примеры решения основных задач.

Предназначен для преподавателей и студентов технических специальностей высших учебных заведений.

УДК 517(075.8) ББК 22.161я73

ISBN 985-418-484-6

	ОГЛАВЛЕНИЕ
Введение ..............................................................................................................		7
МОДУЛЬ 1. Функции нескольких переменных .............................................		9
§ 1.	О функциональных зависимостях
	между несколькими переменными ...........................................................	9
§ 2.	Понятие евклидового пространства R 2 и R3 . Топология R 2 .............	9
§ 3. Примеры и упражнения ...........................................................................		14
§ 4.	Функции двух переменных. Понятие функции n переменных .........	17
§ 5. Предел функции нескольких переменных .............................................		22
§ 6. Непрерывность функции нескольких переменных ..............................		30
§ 7. Дифференцирование функций нескольких переменных .....................		34
§ 8. Дифференцируемость функции нескольких переменных ...................		38
§ 9.	Дифференциал функции нескольких переменных.
	Инвариантность формы первого дифференциала.
	Правила дифференцирования .................................................................	47
§ 10. Функции нескольких переменных, заданные неявно ..........................		52
§ 11. Геометрический смысл полного дифференциала функции
	двух независимых переменных ..............................................................	56
§ 12. Частные производные и дифференциалы высших порядков .............		60
§ 13. Дифференциалы высших порядков .......................................................		65
§ 14. Формула Тейлора для функции двух переменных ..............................		69
§ 15. Экстремумы функций нескольких переменных.
	Необходимые условия. Достаточные условия ......................................	72
§ 16. Условный экстремум функции нескольких переменных ...................		78
§ 17. Наибольшее и наименьшее значения функции
	двух переменных в замкнутой области ...............................................	87
§18. Основные задачи и примеры
	для функции нескольких переменных ...................................................	89
	18.1. Топология плоскости ......................................................................	89
	18.2. Функция двух (нескольких) переменных .....................................	90
	18.3. Предел функции нескольких переменных ...................................	92
	18.4. Непрерывность функции нескольких переменных .....................	94
	18.5. Дифференцирование функций нескольких переменных ............	98
	18.6. Дифференцируемость функции нескольких переменных ........	102
	18.7. Дифференциал функции нескольких переменных.
	Дифференцирование сложных и неявных функций ...........................	105

18.8. Приложения дифференциального исчисления
функций нескольких переменных ........................................................					109
МОДУЛЬ 2. Неопределенный интеграл ....................................................					121
§ 1. Понятие неопределенного интеграла ...................................................					121
1.1. Понятие первообразной функции. Неопределенный интеграл ..					121
1.2. Таблица неопределенных интегралов ...........................................					124
1.3. Свойства неопределенного интеграла ..........................................					124
§ 2. Основные методы интегрирования .......................................................					126
2.1. Метод непосредственного интегрирования .................................					126
2.2. Метод «подведения под знак дифференциала» ...........................					128
2.3. Метод замены переменной или подстановки				...............................	131
2.4. Метод интегрирования по частям		.................................................			135
§ 3. Интегрирование рациональных функций ............................................					141
3.1. Понятие о рациональных функциях ............................................					141
3.2. Интегрирование простейших рациональных дробей ................					143
3.3. Разложение рациональной дроби на простейшие .....................					146
3.4. Интегрирование рациональных дробей ......................................					154
§ 4. Интегрирование выражений,
содержащих тригонометрические функции			........................................		159
4.1. Интегрирование дифференциалов R(sin x, cos x)dx ....................					159
4.2. Интегралы вида	Im,n = ∫sinm x cosn xdx		.........................................		162
4.3. Интегралы вида	In = ∫tgn xdx, In = ∫ctgn xdx .................................				164
4.4. Интегралы вида	I = ∫sin x × cos bxdx , I = ∫cos ax × cos bxdx ,
I = ∫sin ax × sin bxdx ...................................................................................					164
§ 5. Интегрирование выражений, содержащих радикалы .........................					165
			ax + b
5.1. Интегрирование функций вида		R x, n		............................	165

			cx + d
5.2. Интегрирование функций вида		R x,	ax2 + bx + c ....................		166

5.3. Интегрирование функций вида		R (x,	ax2 + bx + c ) ....................		174
5.4.Интегрирование дифференциального бинома ............................					175
5.5.Интегрирование биноминальных дифференциалов ...................					176
5.6.Интегралы, не выражающиеся через элементарные функции ..					178

МОДУЛЬ 3. Определенный интеграл .........................................................	180
§ 1. Задачи, приводящие к понятию определенного интеграла ................	180
1.1.Площадь криволинейной трапеции ..............................................	180
1.2.Работа переменной силы ...............................................................	182
§ 2. Определенный интеграл .........................................................................	183
2.1. Интегральная сумма. Определение определенного интеграла	183
2.2. Основные свойства определенного интеграла ...........................	185
2.3. Определенный интеграл с переменным верхним пределом .....	192
§3. Формула Ньютона-Лейбница ..................................................................	198
§4. Вычисление определенных интегралов .................................................	199
4.1 Вычисление определенных интегралов с помощью
интегральных сумм ..............................................................................	199
4.2. Вычисление определенных интегралов, опираясь
на геометрический смысл определенных интегралов ......................	201
4.3. Вычисление интегралов по формуле Ньютона-Лейбница ........	203
§5. Замена переменной в определенном интеграле ....................................	207
§6. Интегрирование по частям в определенном интеграле .......................	220
§7. Несобственные интегралы .......................................................................	223
7.1. Несобственные интегралы с бесконечными пределами
интегрирования (несобственный интеграл 1 рода) .............................	223
7.2. Свойства и вычисление несобственных интегралов 1 рода .........	226
7.3. Несобственные интегралы от неограниченной функции
на конечном промежутке (несобственный интеграл второго рода) ... 236
7.4. Свойства и вычисление несобственных интегралов
второго рода ..............................................................................................	239
7.5. Особые приемы вычисления несобственных интегралов .............	246
§ 8. Интегрирование как процесс суммирования.
Приложения определенного интеграла .................................................	248
8.1. Общая схема применения интегрального исчисления ................	249
8.2. Вычисление площадей плоских фигур .........................................	249
8.3. Площадь плоской фигуры ..............................................................	257
8.4. Длина дуги плоской кривой ...........................................................	265
8.5. Объем тела .......................................................................................	274
8.6. Объем тела вращения ......................................................................	281
8.7. Площадь поверхности вращения ...................................................	286
8.8. Приложение определенных интегралов к вопросам физики,
механики и техники ...............................................................................	289

§ 9. Приближенное вычисление определенных интегралов ......................	294
9.1. Постановка задачи ...........................................................................	294
9.2. Формула прямоугольников ............................................................	294
9.3. Формула трапеций ..........................................................................	296
9.4. Формула Симпсона .........................................................................	298
МОДУЛЬ 4. Двойной интеграл ...................................................................	301
§ 1. Определение двойного интеграла .........................................................	301
§ 2. Повторный интеграл. Свойства повторного интеграла ......................	304
§ 3. Вычисление двойного интеграла ...........................................................	308
§ 4. Замена переменных в двойном интеграле ............................................	320
§ 5. Двойной интеграл в полярных координатах ........................................	325
§ 6. Приложения двойного интеграла ..........................................................	332
6.1. Вычисление площадей плоских фигур .........................................	332
6.2. Вычисление объемов тел ................................................................	334
6.3. Вычисление площадей поверхностей ...........................................	338
МОДУЛЬ 5. Тройной интеграл ....................................................................	340
§ 1. Задача о вычислении массы тела ...........................................................	340
§ 2. Определение тройного интеграла и условия существования .............	340
§ 3. Свойства интегрируемых функций и тройных интегралов ................	341
§ 4. Вычисление тройного интеграла ...........................................................	342
§ 5. Замена переменных в тройном интеграле ............................................	344
§ 6. Приложения тройного интеграла ..........................................................	352
ЛИТЕРАТУРА ................................................................................................	355

ВВЕДЕНИЕ

Преподавание высшей математики в высших учебных заведениях имеет цель:

−развитие интеллекта и способностей к логическому и алгоритми- ческому мышлению;

−обучение основным математическим методам, необходимым для анализа и моделирования устройств, процессов и явлений при поиске оп- тимальных решений и выбора наилучших способов реализации этих реше- ний; методам обработки и анализа результатов численных и натурных экс- периментов.

Задачи преподавания высшей математики состоят в том, чтобы на при- мерах математических понятий и методов продемонстрировать студентам действие законов материалистической диалектики, сущность научного под- хода, специфику математики и ее роль в осуществлении научно-технического прогресса. Необходимо научить студентов приемам исследования и решения математических формализованных задач, выработать у студентов умение анализировать полученные результаты, привить им навыки самостоятельного изучения литературы по математике и ее приложениям.

Математическое образование современного специалиста включает изучение общего курса математики и специальных математических курсов. Общий курс высшей математики является фундаментом математического образования специалиста, но уже в рамках этого курса должно проводить- ся ориентирование на приложение математических методов в профессио- нальной деятельности. Преподавание специальных разделов ориентирова- но главным образом на применение математических методов к решению прикладных задач. При этом студенты сначала знакомятся с постановкой типичной прикладной задачи, затем изучают общий курс математических задач, к которому относится эта задача, далее – математические методы решения задач данного класса и, наконец, изученные методы применяют для решения исходной задачи. Выбор специальных разделов математики, которые должны изучать студенты, осуществляется с учетом характера их будущей профессиональной деятельности и согласуется с выпускающими кафедрами. Все вопросы преподавания этих разделов специальными ка- федрами должны быть согласованы с кафедрой математики.

В результате изучения курса высшей математики студент должен иметь представление:

−о месте математики в системе естественных наук;

−о математике как особом способе познания мира;

−о содержании основных разделов высшей математики, отличии прикладной математики от фундаментальной.

Знать и уметь использовать:

−методы математического анализа, аналитической геометрии, ли- нейной алгебры, теории функций комплексного переменного и операцион- ного исчисления, теории поля;

−методы решения обыкновенных дифференциальных уравнений. Владеть:

−методами дифференциального и интегрального исчисления;

−методами решения уравнений математической физики;

−аналитическими методами решения прикладных задач.

Иметь навыки:

−аналитического и численного решения уравнений;

−качественного исследования, аналитического и численного реше- ния обыкновенных дифференциальных уравнений;

−самостоятельной смысловой постановки прикладных задач. Программа определяет основное содержание тем и разделов курсов,

подлежащих изучению. Последовательность их изложения и распределе- ния по семестрам, исходя из задач своевременного математического обес- печения общенаучных, общеинженерных и специальных дисциплин и со- хранения логической стройности и завершенности самих математических курсов. При выборе цели ознакомить студентов с максимальным числом математических понятий и методов или выработать у них твердые навыки исследования и решения определенного круга задач. При этом предполага- ется, что глубокое овладение основными понятиями и методами высшей математики позволит студентам освоить те дополнительные разделы, ко- торые им понадобятся в будущем.

В данной книге рассмотрены следующие модули:

−функции нескольких переменных (ФНП);

−неопределенный интеграл;

−определенный интеграл;

−двойной и тройной интегралы.

МОДУЛЬ 1. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ

§1. О функциональных зависимостях между несколькими переменными

При изучении многих вопросов естествознания приходится встре- чаться с такими зависимостями, в которых задействованы несколько пере- менных величин, когда значения одной из этих переменных величин пол- ностью определяются значениями остальных переменных. Так, например, температура Т или плотность ρ тела изменяются при переходе от одной точки данного тела к другой, но так как каждая точка определяется тремя декартовыми координатами x, y, z, то температура Т или плотность ρ оп- ределяются значениями трех переменных x, y и z.

§ 2. Понятие евклидового пространства R 2 и R3 .

Топология R 2

Известные из аналитической геометрии понятия координат точек на плоскости и в пространстве и формула для определения расстояния между двумя точками позволяют ввести аналитическое определение евклидова

пространства R 2 и R3 .
Множество упорядоченных пар				(x, y)	действительных чисел x и y
называется координатной плоскостью, а каждую пару (x, y)								будем назы-
вать точкой этой плоскости и обозначать буквой М. Числа x								и y называ-
ются координатами точки M(x, y).
Координатная плоскость называется евклидовым пространством R2 ,
если для любых двух точек плоскости определено расстояние ρ(M1, M 2 )
по формуле

ρ(M	, M	2	) = (x − x )2 + ( y			2	− y )2 .
1		2	2	1		2	1
Аналогичным образом вводится понятие «евклидово пространство»
R3 . Множество упорядоченных троек (x, y,					z) чисел x, y и z			называется
координатным пространством. При этом каждую тройку (x,								y, z) будем

называть точкой этого пространства и обозначать M(x, y, z). Запись M(x, y,

z) означает, что точка М имеет координаты x, y										и z.
Координатное пространство называется евклидово пространство R3 ,
если для любых		двух			точек		пространства			определено расстояние
ρ(M1, M 2 ) по формуле

ρ(M	1	, M	2	) = (x − x )2 + ( y				2	− y )2	+ (z	2	− z )2 .
	1		2		2	1		2	1		2	1

Введенные выше понятия координатной плоскости и координатного пространства представляют собой аналоги числовой прямой, а R 2 и R3 –

евклидовы пространства –

аналог евклидовой прямой R1 расстояние меж-

ду двумя точками M1 (x1 )

и M 2 (x2 )

определяются по формуле

ρ(M

, M

) = (x − x ) 2

x − x

Множество Е точек (x, y) плоскости R 2 называется окрестностью точки M 0 (x0 , y0 ) , если M 0 является внутренней точкой E, т.е. M 0 вхо-

дит в Е вместе с некоторым кругом:

B(M 0 , r) = {(x, y) (x − x0 )2 + ( y − y0 )2 < r 2 }, r > 0 .

Круг B(M 0 , r) также является окрестностью точки M 0 . Отметим,

что наряду с круговыми окрестностями точки можно рассматривать как квадратные окрестности, так и прямоугольные окрестности точки.

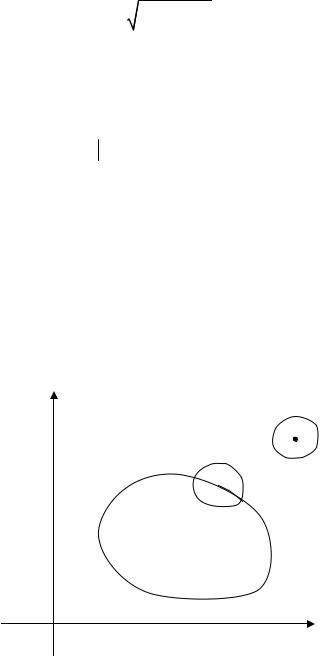
Точка пространства R 2	называется граничной	для множества
E R 2 , если ее любая окрестность содержит как точки из		Е, так и точки,
не принадлежащие Е (рис. 1) –	точка M1 . Точка M 2 –	внешняя точка
множества Е.

Рис. 1

Множество Е называется открытым, если оно служит окрестностью каждой своей точки.

Рассмотрим примеры некоторых множеств.

1 / 361 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

Соседние файлы в папке Высшая математика (РТФ)

#
18.05.20154.76 Mб32умк_Вакульчик_Элементы векторной алгебры.pdf
#
18.05.20155.38 Mб37умк_Вакульчик_Элементы линейной алгебры.pdf
#
18.05.20151.33 Mб39умк_Мальцев_Осн дискретной матем.pdf
#
18.05.20153.75 Mб37умк_Пальчик_Теория вероятностей.pdf
#
18.05.20155.68 Mб31умк_Цывис_Диф.уравнения_Ряды.pdf
#
18.05.20154.7 Mб38умк_Цывис_Функции_Интеграл. исчисл..pdf
#
18.05.20153.54 Mб75умк_Яско_ Диф.уравнения_Ряды.pdf