Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Пензенский Государственный Университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

умк_Цывис_Функции_Интеграл. исчисл

..pdf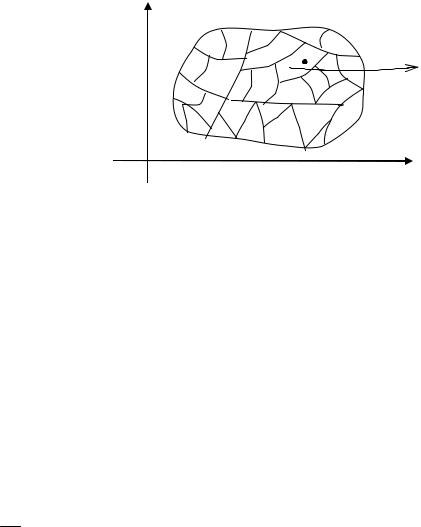

Скачиваний:

Добавлен:

18.05.2015

Размер:

4.7 Mб

Скачать

☆

<<< < Предыдущая 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 3031 / 3631 32 33 34 35 36 > Следующая >>>

МОДУЛЬ 4. ДВОЙНОЙ ИНТЕГРАЛ

§ 1. Определение двойного интеграла

Рассмотрим в плоскости Oxy замкнутую область D, ограниченную линией L. Пусть в области D задана непрерывная функция z = f (x, y) .

Область D	сетью производных кривых (прямых) разбиваем на n
частей, площади которых		Si (i =		) . В каждой из полученных частей
			1, n
выбираем точку	Pi = P(xi , yi )	и найдем значения функции в этих точках

f (Pi ) и составим сумму произведений вида	f (Pi ) × DSi (рис. 1)
	n
Vn = f (Pi ) × DSi + f (P2 ) × DS2 + ... + f (Pn ) × DSn = ∑ f (Pi ) × DSi
	i =1
y
D
Pi	Si

О	x
	Рис. 1

Эта сумма называется интегральной суммой для функции f(x,y) в об- ласти D.

Рассмотрим произвольную последовательность интегральных сумм, построенных с помощью функции f(x,y) для данной области D

Vn ,	Vn	, ..., Vnk	(2)
1	2
при различных способах разбиения области D на части Si .
Если существует конечный предел
			n
V = lim Vnk	=	lim	∑ f (Pi ) × DSi ,
n →∞		n →∞	i =1
(mzx Si →0)		(max Si →0)

независящий от способа разбиения области D на части, от выбора точек

Pi (i =1, n) , то он называется двойным интегралом от функции f(x,y) по области D и обозначается так

301

	∫∫ f (x, y)dS	или ∫∫ f (x, y)dxdy ,
	D			D
т.е. по определению имеем
					n
	∫∫ f (x, y)dxdy = lim ∑ f (Pi )					Si .
	D		n →∞ i i =1
			max S
	Область D называют областью интегрирования.
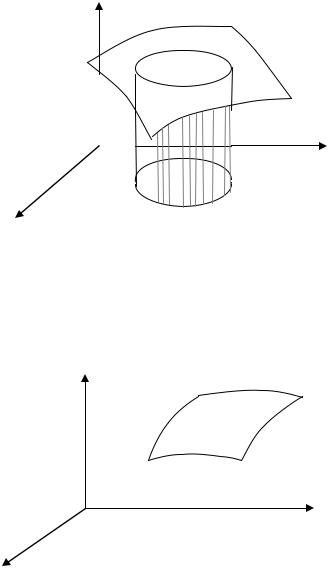
	Геометрический смысл двойного интеграла состоит в следующем:
если	f(x,y) > 0, то двойной интеграл от функции					f(x,y) по области D ра-
вен объему тела Т, ограниченного поверхностью						z = f (x, y) , плоскостью
z = 0	и цилиндрической поверхностью, образующие которой параллельны
оси Oz, а направляющей служит граница области D.
	z
			D
	О					y





	x

Механический (физический) смысл двойного интеграла состоит в сле- дующем: двойной интеграл от функции f(x,y) по области D есть масса пла- стины, ограниченной областью D с плотностью f(x,y) в каждой точке D.

z = f (x, y)

302

Для двойного интеграла справедливы следующие свойства.

Теорема	1. Двойной	интеграл	от	суммы	двух	функций
ϕ(x, y) + ψ(x, y)	по области D	равен сумме двух двойных интегралов по
области D от каждой из функций в отдельности
∫∫(ϕ(x, y) + ψ(x, y))dxdy = ∫∫ϕ(x, y)dxdy + ∫∫ψ(x, y)dxdy .
D		D		D
Теорема 2. Постоянный множитель можно вынести за знак двойного
интеграла: если a – const, то
	∫∫af (x, y)dxdy = a∫∫ f (x, y)dxdy .
	D	D
Теорема 3. Если область		D разбита на две области			D1 и D2 без об-
щих внутренних точек, а f(x,y)		непрерывна во всех точках области D, то
	∫∫ f (x, y)dxdy = ∫∫ f (x, y)dxdy + ∫∫			f (x, y)dxdy		(1)
	D	D1	D2
Доказательство. Интегральную сумму по области D можно пред-
ставить в виде
	∑ f (x, y)DSi = ∑ f (x, y) × DSi + ∑ f (x, y)DS1					(2)
	D	D1	D2

при этом первая сумма содержит слагаемые, соответствующие для области

D1 , вторая –	D2 .
Так как по определению двойно-
го интеграла величина его не зависит						y
от способа разбиения, то, разбивая об-

ласть D	таким образом,				что общая	D1
граница областей		D1	и	D2 является
						D2
границей площадок			DSi , переходя к
пределу в	(2) при		DSi	® 0 получим
равенство (1).						x
Отметим, что доказанная теорема
справедлива для		любого			конечного
числа слагаемых.

303

§ 2. Повторный интеграл. Свойства повторного интеграла

Пусть область D лежит в плоскости Oxy и является областью ин- тегрирования для двойного интеграла. Различают два основных вида об- ласти интегрирования – правильная в направлении оси Oy и правильная в направлении оси Ox.

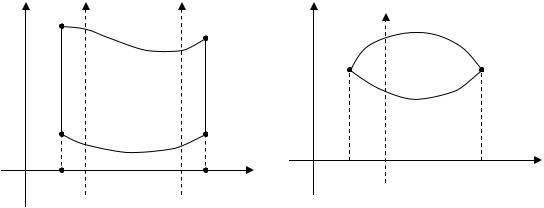
Правильная область в направлении оси Oy –						это область	D на плос-
кости XOY,		ограниченная	снизу линией		y = ϕ1 ( x) , сверху		– линией
y = ϕ2 (x)	(функции ϕ1 (x)		и ϕ2 (x) – непрерывны), слева и справа –					от-
резками прямых x = a и x = b (рис. 1).
y
	A1	y = ϕ2 (x)		y		y = ϕ2 (x)
			B1			y = ϕ2 (x)
			B1
		D			A	D	B
		D
						y = ϕ1 (x)
	A	y = ϕ1 (x)	B					x
			x					x
			x	О	a		b
О	a		b	О	a		b
О	a		b
		Рис. 1				Рис. 2
		Рис. 1
Отметим, что в частных случаях один или оба отрезка							( AA1	или
BB1 ) могут превратиться в точку (рис. 2).
Для правильной области в направлении оси						Oy характерно следую-

щее: область D проектируется в некоторый отрезок [a,b] оси Ox, причем

любая прямая, параллельная оси Oy и проходящая через внутреннюю точ-

ку области D (или через внутреннюю точку отрезка [a,b] ), пересекает гра-

ницу области D (линии y = ϕ1 (x) и y = ϕ2 (x) ) в двух точках (рис. 1, 2).

Отметим, что, если проводить лучи, параллельные оси Oy и одинаково с

ней направленные,		они будут	входить в область	D	на линии
( A1B1 ) y = ϕ1 ( x) –	линия входа в область D в направлении оси				Oy, а вы-
ходить из области	D	на линии	( AB ) y = ϕ2 ( x) – линия выхода из об-

ласти D в направлении оси Oy.

304

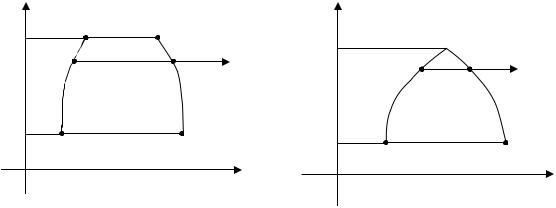
		Правильная область в направлении			оси Ox – это область				D на плос-
кости XOY, ограниченная слева линией					x = ψ1 ( y) , справа –				x = ψ2 ( y)
(функции ψ1 ( y) и				ψ2 ( y) непрерывны), снизу и сверху –				отрезками пря-
мых y = c и y = d.
	y				y
	d		D1	D2	y
	d		D1	D2	d		D1
					d		D1

		x = ψ1( y)		x = ψ2 ( y)
		x = ψ1( y)		x = ψ2 ( y)		x = ψ1( y)	x = ψ2 ( y)
			D			x = ψ1( y)	x = ψ2 ( y)
			D				D
	c						D
	c				c
		C1		C2	c
		C1		C2		C1			C2
				x		C1			C2
	О			x	О				x
					О				x
			Рис. 3			Рис. 4
		В частных случаях один или оба отрезка (C1C2 )					и	(D1D2 ) могут

превратиться в точку (рис. 4). Для правильной области в направлении оси Ox характерно следующее: область D проектируется в некоторый отрезок [c, d ] оси Oy, пересекает границы области D (линии x = ψ1 (t) и x = ψ2 (t) ), не более чем в двух точках (рис. 3, 4). Отметим, что если про-

водить лучи, параллельные оси Ox и одинаково направленные, они будут

входить в область D на линии (C1D1 ) , x = ψ1( y) –	линия входа в область
D в направлении оси Ox, а выходить из области	D на линии (C2 D2 ) ,

x = ψ2 ( y) – линия выхода из области D в направлении оси Ox.

Область, правильную как в направлении оси Ox, так и в направлении оси Oy называют правильной областью.

Пусть функция f(x,y) непрерывна в области D. Выражение вида

	b ϕ2 ( x)
ID	= ∫	∫	f (x, y)dy dx	(1)

	a ϕ1 ( x)
называют повторным (двукратным) интегралом от функции				f(x,y) по об-
ласти D (рис. 1).

Вычисление повторного интеграла (1) начинаем с вычисления инте- грала, стоящего в скобках (внутреннего), причем интегрирование ведется по переменной y, а x считается постоянной. В результате получим непре- рывную функцию от x, т.е.

305

ϕ2	( x)
F(x) = ∫ f (x, y)dy .
ϕ1	( x)

Интегрируя по x полученную функцию в пределах от a до b, по- лучим величину повторного интеграла – некоторое постоянное число

ID = ∫F(x)dx .

1 x2

Пример 1. Вычислить повторный интеграл ID = ∫ ∫

0 0

(x + y)dy dx .

Решение. Построим область интегрирования D. Границы области D оп-

ределяются уравнениями x = 0; x = 1; y = 0; y = x2

y = x2

x= 1

y = 0 x

Искомая область					D –		это «криволинейный» треугольник ОАВ. За-
метим, что область				D правильная как по направлению оси Ox, так и по
направлению оси Oy.
Вычисление данного интеграла начинаем с нахождения внутреннего
интеграла
x2					x2		x2					x2		y		2		x	2	= x3 +			x	4



F = ∫ (x + y)dy ∫ xdy + ∫								ydy = x × y			+														.
F = ∫ (x + y)dy ∫ xdy + ∫								ydy = x × y			+														.
0					0		0				0				2			0			2
0					0		0											0
Тогда
Тогда
			1			x4		x4		x5		1	1				1				7
			1			x4		x4		x5		1	1				1				7
I	D	=	∫	x3	+		dx =		+			=			+					=		.
I		=		x3	+		dx =		+			=			+					=		.
						2				10			4 10 20
			0			2		4		10		0	4 10 20
												0

306

Свойства повторного интеграла

Свойство 1. Если в направлении оси

Oy правильную область

разбить на две области

D2 прямой, параллельной оси

Oy или оси

Ox, то повторный интеграл

по области D будет равен сумме таких же

интегралов по областям

и D2 , т.е.

ID = ID

+ ID .

Доказательство. Пусть прямая

x = c (a < c < b)

разбивает область

D на две правильные в направлении оси Oy области D1

и D2 . Тогда

b ϕ2 ( x)

ϕ2 ( x)

= ∫

∫

f (x, y)dx dy =

F (x)

∫ f (x, y)dx

= ∫ F (x)dx =

ϕ1 ( x)

a ϕ1 ( x)

c ϕ2 ( x)

b ϕ2 ( x)

= ∫ F (x)dx + ∫F (x)dx = ∫

∫

∫ f (x, y)dx

dy = ID + ID .

f (x, y)dx dy + ∫

a ϕ1 ( x)

c ϕ1 ( x)

Таким образом, имеем

ID = ID + I

Следствие. Если область D можно разбить прямыми, параллельными осям координат, на любое число правильных областей D1, D2 ,..., Dn , тогда

ID = ID1

Свойство 2. Если M и m

прерывной в области D функции

+ ID2 + ... + IDn .

наибольшее и наименьшее значения не- f(x,y), тогда (S – площадь области D)

b ϕ2 ( x)			× S
m × S £ ∫	∫	f (x, y)dy dx £ M	× S	(2)

a ϕ1 ( x)
Доказательство. Так как	M наибольшее, m –		наименьшее значения

f(x,y) в области D, то имеем

ϕ2 ( x)

∫

ϕ1 ( x)

ϕ2 (

∫

ϕ1 (

ϕ2	( x)
f (x, y)dy £	∫	M × dy = M × (j2 (x) - j1 (x)) = M × S	(3)
ϕ1	( x)
x)	ϕ2	( x)
f (x, y)dy ³	∫ mdy = m(j2 (x) - j1 (x)) = m × S		(4)
x)	ϕ1	( x)

Из неравенств (3) и (4) следует, что

m × S £ ID £ M × S .

307

Свойство 3. (теорема о среднем). Повторный интеграл ID от не-

прерывной функции f(x,y) по области D с площадью S	равен произведе-
нию площади S на значение функции в некоторой точке P области D, т.е.
ID = f (P) × S	(5)

Доказательство. Так как f(x,y) непрерывна в области D, то она принима- ет наибольшее (M) и наименьшее (m) значения в D, а, следовательно, имеет место неравенство m ≤ f (x, y) ≤ M .

В силу свойства 2 имеем

		m × S £ ID £ M × S
Так как S > 0, то из последнего неравенства имеем
			m £		ID	£ M .

					S
Число	ID	заключено между наибольшим и наименьшим значения-

	S
ми функции	f(x,y), а в силу непрерывности функции f(x,y) в области D
она принимает в некоторой точке P D значение, равное числу							1	× ID ,

							S
т.е. имеет место равенство
			1	× ID = f (P) .

			S
Откуда	ID = f (P) × S .

Что и требовалось доказать.

§ 3. Вычисление двойного интеграла

Теорема. Двойной интеграл от непрерывной функции f(x,y) по пра- вильной области D равен повторному интегралу от данной функции по области D, т.е.

	b ϕ2 ( x)
∫∫ f (x, y)dxdy = ∫		∫	f (x, y)dy dx	(1)

D	a ϕ1 ( x)

Доказательство. Область D прямыми, параллельными осям коор- динат, разбиваем на n правильных областей (прямоугольников), площади которых равны соответственно DS1, DS2 ,...DSn .

Для каждой из этих областей справедлива теорема о среднем (свойство 3)

I	D1	= f (P ) × DS , I		D2	- f (P ) × DS	2	...I	Dn	= f (P ) × DS	n	.
		1	1		2				n

308

В силу свойства 1 для повторного интеграла имеем

			n
ID = ID	+ ID	+	... + ID = ∑ f (Pi ) × DSi .	(2)
1	2		n
			i =1
В правой части равенства (2) стоит интегральная сумма для функции
f(x,y) по области D, предел этой суммы при n → ∞ (max				Si → 0) суще-

ствует и равен двойному интегралу от функции f(x,y) по области D. Вели-

чина повторного интеграла		ID , стоящего в левой части равенства (2), не
зависит от n. Поэтому, переходя к пределу в равенстве (2), получим
ID =		n		= ∫∫ f (x, y)dxdy
ID =	lim	∑ f (Pi )	Si	= ∫∫ f (x, y)dxdy
max Si		→0 i =1		D
	n →∞
или		ID = ∫∫ f (x, y)dxdy .
		ID = ∫∫ f (x, y)dxdy .
		D
Таким образом, имеем
		b ϕ2 ( x)
∫∫ f (x, y)dxdy = ∫			∫	f (x, y)dy dx .

D		a ϕ1 ( x)
Что и требовалось доказать.
Замечание 1. Для случая, когда			f (x, y) ³ 0 формула (1)		имеет сле-
дующее геометрическое истолкование.					z = f (x, y) ,
Пусть существует	тело, ограниченное поверхностью				z = f (x, y) ,

плоскостью z = 0 и цилиндрической поверхностью, образующие которой параллельны оси Oz, а направляющей служит граница области D (рис. 1).

Объем данного тела равняется двойному интегралу от функции f(x,y) по области D:

		V = ∫∫ f (x, y)dxdy		(3)
		D
Вычислим объем данного тела по площадям поперечных сечений.
Проведем плоскость		x = const (a < x < b) , рассекающую данное тело. Дан-
ные плоскости параллельны координатной плоскости				ZOY. Находим пло-
щадь плоской фигуры S(x), получающейся в сечении				x = const .
Эта	фигура –	криволинейная	трапеция, ограниченная линиями
z = f (x, y)	(x − const), z = 0, y = ϕ1 (x), y = ϕ2 (x) , площадь которой выразим
с помощью интеграла		ϕ2 ( x)
		ϕ2 ( x)
		S (x) = ∫	f (x, y)dy .	(4)

ϕ1 ( x)

309

z = f (x, y)

S(x)

y = ϕ2 (x)

y = ϕ1 (x)

a x

Рис. 1

Тогда объем искомого тела

b ϕ2 ( x)
V = ∫	∫	f (x, y)dy dx .	(5)

a ϕ1 ( x)

Вычислим объем этого же тела по площадям поперечных сечений, проводя плоскости y = const (c < y < d ) . Эти плоскости параллельны коор-

динатной плоскости ZOX. Находим площадь плоской фигуры S(y), полу- чающаяся в сечении y = const . Эта фигура – криволинейная трапеция, ог-

раниченная линиями z = f (x, y) (y − const), z = 0, x = ψ1 ( y) , x = ψ2 ( y) ,

площадь которой выразим с помощью интеграла

ψ2	( y)
S ( y) = ∫ f (x, y)dx .		(6)
ψ1	( y)

Тогда объем данного тела

d ψ2 ( y)

V = ∫ ∫

c ψ1 ( y)

f (x, y)dx dy . (7)

В формулах (3), (5)		и (7) левые части равны, следовательно, равны
правые, т.е.
	b j2 ( x)			d ψ2 ( y)
∫∫	f (x, y)dxdy = ∫	∫	f (x, y)dy dx = ∫		∫	f (x, y)dx dy .	(8)

D	a j1 ( x)			c ψ1 ( y)

310

<<< < Предыдущая 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 3031 / 3631 32 33 34 35 36 > Следующая >>>

Соседние файлы в папке Высшая математика (РТФ)

#
18.05.20154.76 Mб34умк_Вакульчик_Элементы векторной алгебры.pdf
#
18.05.20155.38 Mб39умк_Вакульчик_Элементы линейной алгебры.pdf
#
18.05.20151.33 Mб42умк_Мальцев_Осн дискретной матем.pdf
#
18.05.20153.75 Mб40умк_Пальчик_Теория вероятностей.pdf
#
18.05.20155.68 Mб33умк_Цывис_Диф.уравнения_Ряды.pdf
#
18.05.20154.7 Mб40умк_Цывис_Функции_Интеграл. исчисл..pdf
#
18.05.20153.54 Mб77умк_Яско_ Диф.уравнения_Ряды.pdf