Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Пензенский Государственный Университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

умк_Цывис_Функции_Интеграл. исчисл

..pdf

Скачиваний:

Добавлен:

18.05.2015

Размер:

4.7 Mб

Скачать

☆

<<< < Предыдущая 8 9 10 11 12 13 14 15 16 17 18 1920 / 3620 21 22 23 24 25 26 27 28 29 30 31 32 > Следующая >>>

Тогда площадь криволинейной трапеции, выражаемая определенным интегралом равна площади прямоугольника AD1C1 B с тем же основани-

ем AB и с некоторой средней ординатой ML = f(c) в качестве высоты. 12. Обобщенная теорема о среднем значении. Пусть

1. f(x) и g(x) интегрируемы на отрезке [ab];

2.m £ f (x) £ M ;

3.g(x) на [ab] не меняет знак: g(x) ³ 0 (g(x) £ 0) .

Тогда

b	b
∫	f (x) × g(x)dx = μ × ∫ g(x)dx ,	(1)
a	a

где mÎ[m; M ] .

Доказательство. Пусть g(x) ³ 0 и a < b, тогда справедливо неравенство

	mg(x) £ f (x) × g(x) £ M × g(x) .		(2)
Из неравенства, на основании свойства 8, получаем
b	b	b
m ∫ g(x)dx £ ∫ f (x)g(x)dx £ M		× ∫ g(x)dx .	(3)
a	a	a
Так как g(x) ³ 0	для любого x [ab], то в силу свойства 7, имеем
	b
	∫ g(x)dx ³ 0 .		(4)
	a
Если интеграл (4) равен нулю, то из неравенства (3)			следует, что
	b
	∫ f (x)g(x)dx = 0 ,

а, следовательно, исходное утверждение имеет место. Если же интеграл

(4) больше нуля, то разделим на него все части неравенства (3), и полагая

	b
	∫ f (x)g(x)dx
m =	a	,
m =	b	,
	b
	∫ g(x)dx
	a
получим искомое равенство.
Замечание 1. В действительности ограничения, что			g(x) ³ 0 и a < b
не нужны, т.к. перестановка пределов и изменение знака			g(x) не наруша-
ют равенство.

191

Замечание 2. Если функция f(x)		непрерывна на [ab], то формула (1)
имеет вид
b	f (x)g(x)dx =	b
∫	f (x)g(x)dx =	f (c) ∫ g(x)dx ,	(5)
a		a
где c [ab].
Замечание 3. В условии теоремы можно было бы, вместо интегри-
руемости функции f(x)	предположить интегрируемость произведения
f (x) × g(x) .
2.3. Определенный интеграл с переменным верхним пределом
1. Интеграл с переменным верхним пределом. Если функция			f(x)
интегрируема на отрезке	[ab], то для любого x [ab] она интегрируема
на любом отрезке [ax], т.е. для любого x [ab]
	F (x) = x∫ f (t)dt ,		(1)
	a

называют интегралом с переменным верхним пределом. Рассмотрим некоторые свойства функции F(x): а) непрерывность интеграла

Теорема 1. Если функция f(x) интегрируема на отрезке [ab] , то функция F(x) непрерывна на этом отрезке.

Доказательство. Пусть x [ab]		и x +	x [ab]. Докажем, что
DF (x) = F (x + Dx) - F (x) ® 0			при Dx ® 0 .
		x + x	x
DF (x) = F (x + Dx) - F (x) = ∫ f (t) - ∫ f (t)dt =
		a	a
x	x + x	x	x + x
= ∫ f (t)dt + ∫ f (t)dt - ∫ f (t)dt = ∫ f (t)dt.
a	x	a	x
Так как функция	f(x) интегрируема на отрезке [ab], то она ограни-

чена, т.е.

$M > 0; "x Î[ab] ® f (x) £ M .

Тогда

DF (x)	£	x+ x			£ M × Dx .
		x+ x
		∫	f (x)	dx
		x

192

Откуда получаем, что DF (x) ® 0 при Dx ® 0 , т.е. функция F(x)

непрерывна в точке x. Но так как

x – произвольная точка отрезка

[ab], то

F(x) непрерывна на отрезке [ab];

б) дифференцируемость интеграла

Теорема 2. (Теорема Барроу). Если функция

f(x)

интегрируема на

отрезке [ab] и непрерывна в точке x [ab], тогда функция

F (x) = x∫ f (t)dt

(1)

дифференцируема в точке x, причем

′

F (x) = f (x) .

Доказательство. Пусть Dx ¹ 0 и x +

x [ab], тогда

x + x

DF (x)

F (x + Dx) - F (x)

∫ f (t)dt - ∫ f (t)dt

F ¢(x) = lim

= lim

x →0

x + x

∫ f (t)dt + ∫ f (t)dt - ∫ f (t)dt

∫ f (t)dt

= lim

x →0

x + x

f (t)dt = f (c) × (x + Dx - x)

= lim

f (c) × Dx

∫

x < c < x + x

x →0

т.к. f (t) -

= lim f (c) =

= f (x).

x →0

непрерывна

Таким образом, получили, что

′

F (x) = f (x) .

Доказанная теорема имеет огромнейшее теоретическое и прикладное

значение. Если предположить, что функция

f(x) непрерывна на отрезке

[ab], то она интегрируема и, следовательно, установленное выше утвер-

ждение справедливо для любой точки	x [ab]; производная от интеграла
(1) по переменному верхнему пределу	x равна значению f(x) подынте-

гральной функции на этом пределе. Другими словами, для непрерывной на [ab] функции f(x) всегда существует первообразная; примером которой является определенный интеграл (1) с переменным верхним пределом..

193

Замечание. Утверждения, доказанные выше имеют место и для слу- чая интеграла с переменным нижним пределом, т.к.

				a	x
				∫ f (t)dt = -∫ f (t)dt .
				x	a
Пример 1. Найти производную по x						от функций:
	F (x) =	x2				F (x) =	x2
1.	F (x) =	∫ ln tdt, x > 0 ;			2.	F (x) =	∫ ln tdt, x > 0 ;
		1					x2

3.	F (x) = ∫x sin t 2 dt, x > 0 .
			1

Решение. Для решения данных задач будем использовать правило диффе- ренцирования сложной функции и теорему о производной интеграла с пе- ременными верхним пределом.

1. F ¢(x) =	x∫2ln tdt		¢ × (x	2 )¢
x				x
	1	x2

2. Fx¢(x) =	x2					′	c
2. Fx¢(x) =	∫	ln tdt				=	∫ ln tdt

	x2					x	x2
					′	x
x3					′	× (x3 )x¢		x2
= ∫ ln tdt						× (x3 )x¢		- ∫
				3
c			x	3				c
			x

= 9x2 ln x - 4x ln x.

Итак Fx′ (x) = x × ln x(9x - 4) .

= 2x × ln x 2 = 4x ln x ;

x3		′		x2		x3	′		=
+ ∫ ln tdt				=	- ∫ ln tdt +	∫	ln tdt		=
c					c	c
c			x		c	c		x
		′	x					x
		′
ln tdt		× (x2 )¢ = 3x2 ln x3 - 2x ln x2 =
		2
	x	2
	x

3. Так как

F (x) = ∫x sin t 2 dt = c∫ sin t 2 dt + ∫x sin t 2 dt = - x∫ sin t 2 dt + ∫x sin t 2 dt .

′

Тогда F¢(x) = - ∫sin t2dt

+ ∫

sin t 2dt

(

x )

-1

sin

sin x

= -sin

+ sin x ×

2 x

194

sin

Итак F ¢(x) =

x 2

sin

Пример 2. Найти

′

, если функция задана параметрически

y x

t 3

x = ∫ 3 z ln z

ln zdz

y = ∫ z

Решение. Для решения данной задачи будем использовать правило диф- ференцирования функции, заданной параметрически и теорему о произ- водной интеграла с переменным верхним пределом.

yt ′

, то находим

′

Так как

y x

и yt

xt ¢

′

xt¢ =

∫ 3

ln zdz

× (t3 ) ¢ = t ln t3 × 3t2 = 9t3 ln t.

¢ =

∫

z2 ln zdz

(

t ) ¢ = -t ln t ×

= -

1 t

ln t.

а, следовательно, искомая производная

y x¢ =

9t 3 ln t

= -36t 2

= -36t 2 , t > 0 .

t ln t

Пример 3. Найти производную

y x

функции, заданной неявно

∫ et dt + ∫ cos tdt = 0 .

Решение. Дифференцируем обе части равенства по переменной x, считая

y – сложной функцией x, получим						e y × y x ′ + cos x = 0 .
Откуда			y x ¢ = -	cos x	= -e − y	cos x .
Откуда			y x ¢ = -		= -e − y	cos x .
				e y
Итак		y x ′ = -e − y cos x .
Пример 4. Найти производную y x′							функции, заданной неявно
y	−t	2	x 2				x			y
y		2	x 2			2.	x	- 2 sin 2		y
1. ∫e			dt + ∫ sin 2 tdt = 0 ;			2.	∫ 3	- 2 sin 2	zdz + ∫ cos tdt = 0 .
1			1				π		0
							4

195

Решение. 1. Дифференцируем обе части равенства по

x, считая

y = y(x) –

сложной функцией:

¢ × (x 2 )x¢ = 0

y∫ e −t 2

× y x ¢ + x∫ sin

2 tdt

e − y2

× y¢ + 2x sin 2 x 2 = 0

Решая полученное уравнение относительно y x′ ,

получим

y¢ = -2xe y 2

× sin 2 x 2

2. Ответ: y¢ = -

3 - 2 sin 2

cos y

Пример 5. Определить точки экстремума функции F (x) =

x sin t

∫

dt в

области x > 0.

Решение. Находим критические точки

F(x)

F ¢(x) =

sin x

: F ′(x) = 0 при

sinx = 0 x = πn .

Находим F ′′(x) в этих точках

F ¢¢(x) =

x cos x − sin x

F ¢¢(pn) =

(-1)n

;

cos(np) =

¹ 0 .

Так как

′′

то

x = πn –

точки экстремума, а именно: если

F (pn) ¹ 0 ,

n = 2m (четное), то x = πn –

точки максимума

F (πn) > 0 ; если n = 2m + 1

(нечетное), то точки x = πn –

точки минимума F (πn) < 0 .

Пример 6. Найти точки экстремума и точки перегиба функции

y = x∫ (t - 1)(t - 2) 2 dt

Ответ: точка минимума при x = 1; точки перегиба

x =

: x = 2 .

∫ cos x 2

Пример 7. Найти предел

lim

dx .

x→0

Решение. При вычислении данного предела используем правило Лопиталя

	x	2 dx
	∫ cos x			0		cos x 2		1
lim	0		=		= lim		=		= 1.
	x					1
x→0				0	x→0			1

196

Пример 8. Найти пределы:

sin x

∫ sin

xdx

∫

tgxdx

lim

;

lim

;

x→0

x 3

x →0 tgx

∫

sin xdx

(arg tgx)

∫ e x

∫

lim

;

lim

x→+∞

2 x

x →+∞

x2 +1

∫ e

Решение.

∫ sin

xdx

2x sin x

1. lim

= lim

3x 2

x→0

2. Ответ: 1.

3. Имеем неопределенностьвида

∞

. Применяяправило Лопиталя, получим

∫ex

2 × ∫ex2 dx × ex2

lim

2 x2

x →+∞

2 x

x →+∞

∫e

2 dx

2∫ex

2ex

= lim

= 0

x →+∞

× 2x

Замечание. Вторая теорема о среднем.

Приведем еще одну теорему, относящуюся к интегралу от произве- дения двух функций

I = ∫ f (x)g(x)dx .

1. Если на отрезке [ab] (a < b) f(x) монотонно убывает и неотрица-

тельна, а g(x) – интегрируема, тогда

b	c
∫ f (x)g(x)dx = - f (a)∫ g(x)dx ,		(2)
a	a

где c [ab].

197

2. Если на отрезке [ab] (a < b)	f(x) монотонно возрастает и неот-
рицательна, а g(x) – интегрируема, тогда
b	b
∫ f (x)g(x)dx =	f (c) ∫ g(x)dx ,
a	c
где c [ab].
§3. Формула Ньютона-Лейбница
Теорема 1. Если f(x) непрерывна на отрезке [ab] и пусть F(x)		яв-
ляется какой-либо ее первообразной на этом отрезке, тогда
b
∫ f (x)dx = F (b) − F (a) .		(1)

Доказательство. Для непрерывной на отрезке [ab] функции f(x) интеграл

x
F (x) = ∫ f (t)dt + C	(2)
a
является первообразной функцией. Полагая в формуле (2)	x = a, получим
F(a) = C, т.е.
x
F (x) = ∫ f (t)dt + F (a)	(3)

полагая в выражении (3) x = b, получим

∫ f (x)dx = F (b) − F (a) .

Что и требовалось доказать.

Замечание. Формулу Ньютона-Лейбница называют основной форму- лой интегрального исчисления.

Замечание. Если применить к интегралу с переменным пределом теорему о среднем и вспомнить, что F ′(x) = f (x) , получим

F (b) − F (a) = f (c)(b − a) = F ′(c)(b − a), c [ab] ,

а это формула Лагранжа для функции F(x).

Таким образом, с помощью формулы Ньютона-Лейбница устанавли- вается связь между теоремами о среднем в дифференциальном и инте- гральном исчислении.

198

§4. Вычисление определенных интегралов

4.1.Вычисление определенных интегралов

спомощью интегральных сумм

Пусть требуется вычислить определенный интеграл от непрерывной функции f(x) на [ab]. Для этого строим интегральную сумму для f(x) на [ab] и находим соответствующий предел полученной интегральной суммы, тем самым находим определенный интеграл.

			1
Пример 1. Вычислить определенный интеграл I = ∫ xdx .
			0
Решение. Из определения определенного интеграла имеем
1	n−1		n−1
∫ xdx = lim ∑ f (εi ) x =		lim	∑ f (εi ) x ,
0	n→∞ i=1	max x→0	i=1

где 1.

0 = x0 < x1 < x2 < ...< xn = 1,

ei×Î[xi×xi+1];

xi = xi+1 –

xi.

Отрезок [0,1] разбиваем на n равных частей (в общем случае не

обязательно)

(i =

) ,

Dx =

® 0 , при

точками деления

1, n

при этом

n → ∞ .

В качестве точек ei выбираем правые точки отрезков [ x i ; x i+1 ]

ei = xi+1 =

i + 1

: (i =

0, n -1) .

4. Тогда интегральная сумма имеет вид

n−1 i +1

n(n +1)

Sn = ∑

(1 + 2 + 3 + ... + n) =

2n2

i=1 n

I = lim Sn = lim

n(n + 1)

n →∞

2n2

Значит

I = ∫ xdx =

Замечание 1. В данном примере можно выбрать точки ei другим спосо- бом, а предел интегральной суммы будет тот же. Действительно, если в каче-

стве ei выбрать середины отрезков [ x i ; x i+1 ] (i = 0, n −1) , т.е. εi = (i + 1 ) 1 . 2 n

199

Тогда интегральная сумма имеет вид

n−1

2i +1

2n2

Sn = ∑

+ 3 + 5 + ... + (2n -1)] =

2n2

4n2

i=1

2n n

откуда имеем, что

limSn

, т.е.

∫ xdx =

n→∞

Пример 2. Вычислить определенный интеграл I = ∫exdx .

Решение. Отрезок [01] разбиваем на n равных частей точками

= 0 < x1 =

... < x

< .. = x

=1.

Длина каждого из отрезков [xk, xk+1] равна Dx

. Выбираем ek = xk =

( k =

f (ek ) = e

(k =

0, n -1). Тогда

0, n -1) ,

а интегральная сумма Sn будет

n−1

e -1

равна S

= ∑ e n ×

= (1 + e n + en + ... + e n

)

(сумма

членов гео-

k =0

e n -1

lim Sn = lim

= e -1 так

метрической прогрессии b0 = 1 q = e n ). Тогда

n →∞

en -1

как lim

= lim

=1.

n →∞

х→0 ex -

х→0 ex

e n -1

Таким образом, I = ∫exdx = e -1.

Пример 3. Вычислить определенный интеграл

I = ∫

Решение. В силу определения определенного интеграла (произвольным способом разбиваем отрезок интегрирования, произвольно выбираем точки деления, строим интегральную сумму) её предел, если существует, то он не зависит от способа разбиения и выбора точек. Отрезок [1;2] разбиваем на n

частей так, чтобы точки деления xi (i = 0, n) составляли геометрическую прогрессию со знаменателем q = n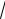2 , т.е. x0 = 1 x1 = q x2 = q2 … xn = qn = 2.

200

<<< < Предыдущая 8 9 10 11 12 13 14 15 16 17 18 1920 / 3620 21 22 23 24 25 26 27 28 29 30 31 32 > Следующая >>>

Соседние файлы в папке Высшая математика (РТФ)

#
18.05.20154.76 Mб33умк_Вакульчик_Элементы векторной алгебры.pdf
#
18.05.20155.38 Mб38умк_Вакульчик_Элементы линейной алгебры.pdf
#
18.05.20151.33 Mб40умк_Мальцев_Осн дискретной матем.pdf
#
18.05.20153.75 Mб39умк_Пальчик_Теория вероятностей.pdf
#
18.05.20155.68 Mб32умк_Цывис_Диф.уравнения_Ряды.pdf
#
18.05.20154.7 Mб39умк_Цывис_Функции_Интеграл. исчисл..pdf
#
18.05.20153.54 Mб76умк_Яско_ Диф.уравнения_Ряды.pdf