Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Пензенский Государственный Университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

умк_Цывис_Функции_Интеграл. исчисл

..pdf

Скачиваний:

Добавлен:

18.05.2015

Размер:

4.7 Mб

Скачать

☆

<<< < Предыдущая 12 13 14 15 16 17 18 19 20 21 22 2324 / 3624 25 26 27 28 29 30 31 32 33 34 35 36 > Следующая >>>

Данную теорему можно коротко сформулировать следующим обра- зом: прибавление (вычитание) под знаком интеграла абсолютно интегри- руемой функции не влияет ни на сходимость интеграла, ни на характер сходимости (абсолютная, условная сходимость).

Теорема 3 (признак Дирихле сходимости интегралов).

Если функция f(x) непрерывна, а функция g(x) имеет непрерывную производную на промежутке [a; +∞) и выполняются следующие условия:

		x
1) функция F (x) = ∫ f (t)dt			(первообразная для	f(x)) ограничена на
		a
промежутке		[a; +∞) ;
2) функция g (x) не меняет знак на [a; +∞) , т.е. g (x) £ 0 или g (x) ³ 0 ;
	′		′	′
3) lim g(x) = 0 .
x→+∞		+∞
		+∞
Тогда интеграл		I = ∫ f (x) × g(x)dx сходится.
		a
Замечание. Условия (2) и (3) в теореме 3 означают, что функция g(x)
монотонно стремится к нулю при			x → +∞ .
Следствие (признак Абеля). Если функция f(x)				непрерывна на про-
		+∞
межутке	[a; +∞) , интеграл I = ∫		f (x)dx сходится, а функция g(x) огра-
		a
ничена на			′
ничена на	[a; +∞) и ее производная g (x) не меняет знак на этом проме-
		+∞
жутке [a; +∞) , то интеграл I = ∫			f (x) × g(x)dx сходится.

6.Признаки сходимости несобственных интегралов, основанные на их сравнении.

Пусть функция f (x) ³ 0 определена на промежутке [a; +∞) и ин-

тегрируема на любом конечном промежутке [a;c) . Тогда имеет место сле-

дующая теорема.

Теорема. Если при x ³ a справедливо неравенство 0 £ f (x) £ j(x) , то из

+∞	+∞
сходимости интеграла ∫ j(x)dx следует сходимость интеграла	∫ f (x)dx , а из
a	a
+∞	+∞

расходимости интеграла ∫ f (x)dx следует расходимость интеграла	∫ j(x)dx .
a	a

231

+∞

Доказательство. Пусть интеграл ∫ ϕ(x)dx сходится, тогда

						a
		c				c	+∞
F (c) = ∫ f (x)dx ≤ ∫ϕ(x)dx ≤ ∫ ϕ(x)dx = I .
		a				a	a
Функция F (c) монотонно возрастает и ограничена конечным числом I,
следовательно, для	F (c) при				c → +∞ существует конечный предел, а это
		+∞
значит, что интеграл		∫ f (x)dx			сходится. Что и требовалось доказать.
		a
Следствие 1. Если существует предел
		lim		f (x)		= c	(0 < c < +∞) ,
		lim				= c	(0 < c < +∞) ,
		x→+∞ ϕ(x)
+∞					+∞
то оба интеграла	∫	f (x)dx		и	∫ ϕ(x)dx сходятся или расходятся одно-
	a				a
временно.
Следствие 2	(признаки Коши).
Если для достаточно больших x							функция f(x) имеет вид
			f (x) =			g(x)	(k > 0) ,
			f (x) =			xk	(k > 0) ,
						xk
		g(x) ³ c > 0 , то интеграл						+∞
тогда: 1) если k > 1	и	g(x) ³ c > 0 , то интеграл						∫ f (x)dx сходится;
								a
2) если 0 < k £1, g(x) ³ c > 0 , то интеграл								+∞
2) если 0 < k £1, g(x) ³ c > 0 , то интеграл								∫ f (x)dx расходится.

Замечание. По отношению к знакопеременной функции f(x) приве- денные признаки не применимы. Но с помощью них можно установить сходимость интеграла от положительной функции f (x) : если эта функ-

ция оказывается интегрируема, то функция f(x) также будет интегрируе- ма, притом абсолютно.

Отметим, что если функция f(x) абсолютно интегрируема на проме-

жутке [a; +∞), а функция g(x) ограничена, то функция f (x) × g(x) будет абсолютно интегрируема на [a; +∞).

232

Доказательство этого утверждения следует из неравенства

f (x) × g(x)

£ L ×

f (x)

+∞ cos ax

Например, для интеграла

I = ∫

имеем, что

функция

0 1 + x2

f (x) =

абсолютно интегрируема, а функция

g(x) = cos ax

ограни-

1 + x2

чена. Отсюда следует абсолютная сходимость данного интеграла.

Таким образом, для знакопеременной функции ранее изложенные соображения – в благоприятном случае – могут установить только абсо- лютную сходимость. Если интеграл от данной функции расходится или сходится, но не абсолютно, то различить эти случаи, используя установ- ленные здесь признаки, невозможно.

Замечание (более тонкий признак сходимости несобственных инте- гралов). Данный признак позволяет устанавливать сходимость несобствен- ных интегралов в ряде случаев, когда абсолютная сходимость отсутствует.

Пусть функции f(x)

и g(x)

определены на промежутке

[a; +¥),

причем f(x)

интегрируема в каждом конечном промежутке [a;c) . Если

интеграл

F (c) = ∫ f (x)dx –

ограниченная

функция от

c, а функция g(x) –

монотонная,

причем

g(x) → 0

x → +∞ , то интеграл

+∞

при

∫

f (x)g(x)dx

сходится.

Пример 8. Исследовать на сходимость интегралы:

+∞ arctgx

+∞

1. ∫

dx ;

∫

x(x - 2)(x - 3)

Решение:

1. Подынтегральная функция при

x → +∞ – бесконечно малая перво-

го порядка, т.е. сравнима с функцией вида

; тогда интеграл расходится.

2. Подынтегральная функция при

x → +∞ –

бесконечно малая по-

рядка

; тогда интеграл сходится.

233

+∞ cos6 5x

Пример 9. Исследовать на сходимость интеграл

I = ∫

7 1 + x8

Решение. Так как при x ³1 выполняется условие 0 £

cos6

а ин-

7 1 + x8

+∞ dx

x 7

теграл ∫

сходится, то будет сходиться и исходный интеграл I.

x 7

+∞

Пример 10. Исследовать на сходимость интеграл

I = ∫

× ln

Ответ: 1) если a > 1, b – любое число, то интеграл I сходится;

2)если a = 1, b > 1, то интеграл I сходится;

3)если a = 1, b £1, то интеграл I расходится;

4) если a < 1, b – любое число, то интеграл I расходится.

∞	dx
Пример 11. Исследовать на сходимость интеграл I = ∫
		.

−∞ x2	+ 4x + 5

Решение. В данном интеграле пределы интегрирования бесконечны, по- этому предварительно разбиваем данный интеграл на два:

∞

+∞

I = ∫

∫

+ ∫

(x +

2)2 + 1

2)2 +

−∞ x2 + 4x + 5

−∞

0 (x

= lim ∫

lim

∫

a → −∞ a

(x + 2)2

+ 1

b →+∞

(x + 22 + 1

= lim

arctg(x + 2)

+ lim arctg(x + 2)

= p

a → −∞

I = p .

a b →+∞

Таким образом,

Пример 12. Исследовать на сходимость интеграл Дирихле

+∞ sin x
I = ∫		dx .
	x
0

Решение. Данный интеграл I находится следующим образом

+∞ sin x		π		+∞ sin x
+∞ sin x		2 sin x		+∞ sin x
I = ∫		dx = ∫		dx + ∫		dx .
I = ∫		dx = ∫		dx + ∫		dx .
0	x	0	x	π	x
				2

234

Первый интеграл собственный (обычный определенный интеграл,

т.к.

lim

sin x

=1) и следовательно на сходимость исходного интеграла он

x→0

не влияет. Второй интеграл интегрируем по частям и получим

+∞ sin x

cos x

+∞

+∞ cos xdx

+∞ cos x

∫

= -

- ∫

= - ∫

= I1 .

Но несобственный интеграл

сходится, и притом абсолютно, так

как справедливо неравенство

cos x

+∞ dx

а интеграл

∫

сходится.

0 x

Следовательно, исходный интеграл I сходится.

+∞ sin x

Докажем,

что интеграл

I = ∫

сходится условно, т.е. инте-

+∞

sin x

sin

- cos 2x

грал

∫

расходится. Так как

+∞

1 - cos 2x

+∞ dx

+∞ cos 2x

Но интеграл ∫

∫

расходится, т.к.

+∞ dx

+∞ cos 2x

интеграл

∫

–

расходится, а интеграл

∫

dx –

сходится.

π x

Следовательно,

искомый интеграл I

сходится условно.

Пример 13. Исследовать на сходимость интегралы

+∞

cos 2x

1. I = ∫ e−2 x2 dx ;

2. I = ∫

dx ;

I = ∫

+ sin x

x2 + x

Решение: 1. Для решения задачи используем признак сравнения. Функция

e−2 x2 > 0	для любого x Î[0; +¥) . Неравенство e−2 x2 < e− x для x ³1, по-
этому I	представим в виде
	+∞	1	+∞
	∫ e− x	2 dx = ∫e− x2	+ ∫ e− x2 dx .
	0	0	1

235

Первый из двух интегралов правой части собственный, а следова- тельно сходится. Для второго интеграла имеем

+∞	+∞		1
∫	e− x2 dx ≤ ∫	e− xdx =		.

1	1		e

Следовательно, сходится. Тогда искомый интеграл сходится.

2. Так как функция f (x) =

> 0

для

x ³1, то f(x) является

x3 + sin x

б.м.ф. при x → +∞ . Сравнивая ее с функцией

ϕ(x) =

получим

+ sin x

∞

sin x

lim

= lim 1

= 1.

x→+∞

∞

x→∞

+∞ dx

Но так как ∫

расходится, то, значит, исходный интеграл так же

1 x

является расходящимся.

x [2;+∞)

3. Подынтегральная функция для

меняет знак, если ме-

няется знак числителя, поэтому применять признак сравнения невозможно, но можно провести исследование на абсолютную сходимость интеграла

+∞

cos 2x

= ∫

dx .

x2 +

Так как имеет место неравенство

cos 2x

≤

для x ³ 2 , а инте-

x2 + x

+∞ dx

грал ∫ сходится, то исходный интеграл сходится абсолютно.

2 x2

7.3. Несобственные интегралы от неограниченной функции на конечном промежутке (несобственный интеграл второго рода)

1. Пусть функция f (x) определена на конечном промежутке [a;c]

при любом c Î[a;b) . Если существует конечный предел lim	c
	∫ f (x)dx , то
c→b−0	a

этот предел называют несобственным интегралом от неограниченной функ- ции f (x) на промежутке [a;b) . Таким образом, по определению имеем

b		c
∫ f (x)dx =	lim	∫ f (x)dx .	(1)
a	c→b−0	a
a		a

236

Если существует конечный предел (1) то интеграл ∫ f (x)dx называ-

ется сходящимся, если предел (1) не существует или равен бесконечности то данный интеграл называется расходящимся.

2. Аналогично, для функции	f (x)	определенной на конечном про-
межутке [a;b) и интегрируемой	на любом отрезке [c;b]			при любом
c [a;b) , то по определению принимают
b			b
∫ f (x)dx = lim			∫ f (x)dx .	(2)
a	c→a+0		c
a			c

Если предел (2) существует и конечный, то несобственный интеграл называется сходящимся; в противном случае – расходящимся.

3. Если функция f (x) определена на конечном интервале (a;b) ин-

тегрируема на отрезке [m;n] , [m;n] (a;b) то несобственный интеграл от функции f (x) на (a;b) определяется формулой

b		m
∫ f (x)dx =	lim	∫ f (x)dx .	(3)
a	m→a+0	n
a	n→b−0	n
Если предел (3) существует и он конечный, то несобственный инте-
грал называется сходящимся, в противном случае – расходящимся.
4. Если функция f (x) определена на отрезке [a;b]			за исключением точ-

ки c (a;b) , и интегрируема на отрезках [a;m]				и [n;b] при любых m и n
таких, что a ≤ m < c < n ≤ b ,	то несобственный интеграл от функции					f (x)
на [a;b] определяется равенством
b		m	f (x)dx + lim		b
∫ f (x)dx =	lim	∫	f (x)dx + lim		∫ f (x)dx .	(4)
a	m→c−0	a	n→c+0		n
a		a			n

Если оба предела в правой части выражения (4) существуют и ко- нечны, то интеграл называется сходящимся, и имеет место равенство

b	c	b
∫ f (x)dx = ∫ f (x)dx + ∫ f (x)dx .
a	a	c
5. Если функция f (x)	не определена на конечном промежутке (a;b)

за исключением точек xk (k = 1, n), где a = x0 < x1 < ...xn = b , то несобствен-

ный интеграл ∫ f (x)dx понимается как сумма несобственных интегралов

237

по промежуткам ( xk −1, xk )(k = 1, n), и по определению считается сходя-

щимся по всем промежуткам ( xk −1, xk ) (k = 1, n) . Если хотя бы по одному промежутку ( xk −1, xk )(k = 1, n) имеем расходимость, то исходный интеграл

является расходящимся.

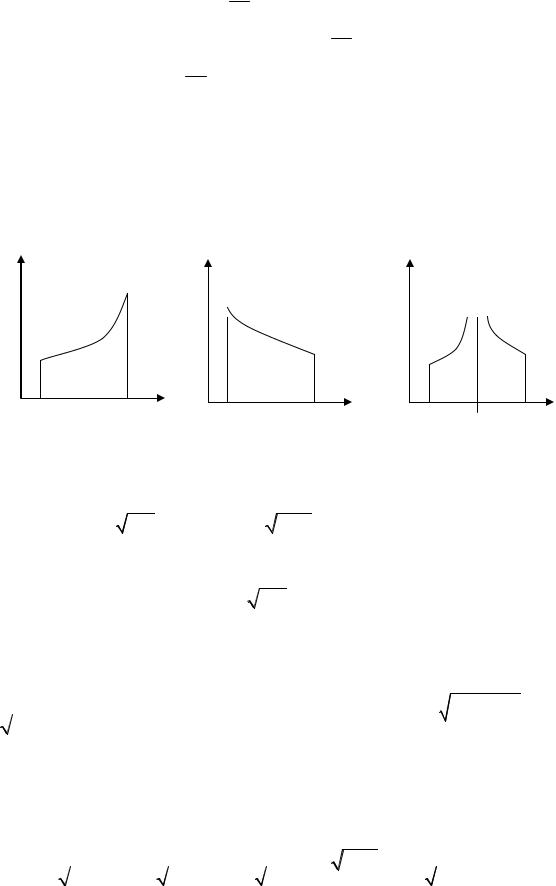
С геометрической точки зрения несобственный интеграл второго ро- да означает следующее: площадь фигуры, ограниченной кривой y = f (x) и

прямыми x = a, x = b ( x → b − 0; x → a + 0; x → c ± 0) , имеет конечную пло-

щадь S .

y		y	y

	y = f (x)	y = f (x)	y = f (x)

b –0	x		a + 0	x		c – 0		c + 0 x
b –0	x		a + 0	x		c – 0		c + 0 x
a	b	a		b	a		c	b

Пример 14.

Вычислить несобственный интеграл

14.1)

14.2) I =

− 2

14.3) I =

+ 2

I = ∫

;

∫

dx;

∫

dx.

1 x 5 ln x

x − 1

−1

x 3

Решение. 14.1)

функция f (x) =

неограничена в окрестности точки

x 5 ln x

x = 1. На любом отрезке [1 + ε;e], ε > 0

функция интегрируема, так как она

непрерывна. Следовательно

ln−

= lim

xd ln x = lim

= lim

1 −

5 ln

4 (1 + ε)

∫

1 x

ln x

ε→+0

1+ ε

ε→+0 4

1+ ε

ε→+0 4

Значит, данный интеграл сходится и его величина равна

;

14.2)

так как данный интеграл I

можно представить в виде

x − 2

x − 1

I = ∫

dx = ∫

dx − ∫

∫ x − 1dx − ∫

= I1 + I

2 .

x −

x − 1

238

В интеграле I1 подынтегральная функция непрерывна на отрезке

[1;2] поэтому

	2			1			3			2
							3			2

						2(x	-1)2					2
	I1 = ∫	(x -1)2 dx =				2(x	-1)2			=		2	.
	I1 = ∫	(x -1)2 dx =					3			=		3	.
	1						3					3
	1
										1
										1
Интеграл I2 несобственный, подынтегральная функция неограни-
ченна в окрестности точки		x = 1, поэтому
		2	dx						2
	= lim	2			= lim 2						= 2.
I2		∫						x -1


	ε→+01+ε		x -1		ε→0						1+ε
	ε→+01+ε		x -1		ε→0						1+ε

Тогда I = 2 - 2 = - 4 ; 3 3

14.3) так как

3x2

+ 2

−

I = ∫

= 3 ∫

x 3 dx + 2 ∫

x 3 dx = 3 ×

x 3

+ 2 ∫

x 2 dx =

+ 2 × I1 .

−1

x 3

x = 0

Так как

I1 –

несобственный интеграл,

– точка разрыва, поэтому

0 − ε

I2 = ∫ x−

dx = ∫ x−

dx + ∫ x−

∫ x−

3 dx = lim

3 dx + lim

3 dx = 3 + 3 = 6.

−1

ε→+0

−1

ε→+0

0 + ε

Тогда

I =

+12 =

102

7.4. Свойства и вычисление

несобственных интегралов второго рода

Будем расследовать несобственные интегралы вида

I = ∫ f (x)dx

(1)

предполагая, что:

[a;b), где a и

1) функция

f(x)

определена на промежутке

b –

ко-

нечные точки;

[a;c]

2) функция

f(x)

интегрируема по Риману на отрезке

при

лю-

бом c Î[a;b) .

239

1. Линейность интеграла.

Если сходятся несобственные интегралы от функций f(x) и			g(x) на
промежутке [a;b) , то при любых l,	mÎ R	сходится интеграл от функции
lf (x) ± m × g(x) на промежутке [a;b)	и выполняется равенство
b	b	b
∫(lf (x) ± mg(x))dx = l∫ f (x)dx ± m∫ g(x)dx .
a	a	a
2. Формула Ньютона-Лейбница.
Если функция f(x) непрерывна на промежутке [a;b) , F(x) –			перво-

образная для f(x), то несобственный интеграл (1) сходится тогда и только тогда, когда существует конечный предел

lim F (c) = F (b − 0) ,	(2)
c→b−0
причем
b
∫ f (x)dx + F (b - 0) - F (a) .	(3)
a
Формула (3) называется формулой Ньютона-Лейбница для несобст-
венного интеграла.
Замечание. Говоря о первообразной функции F(x)	можно понимать

в широком смысле: F(x) должна иметь своей производной f(x) везде, ис- ключая не только особые точки, но и, быть может, еще некоторые точки в конечном числе, лишь бы в них не нарушалась непрерывность F(x).

Пример 15. Исследовать на сходимость интеграл

I = ∫

3 x

−1

Решение. Особая точка функции

f (x) =

x = 0. Так как первообразная

3 x

функция F (x) =

непрерывна и в этой точке x = 0,

то интеграл I су-

ществует, т.е.

× x 3

= 4,5 .

∫

3 x

−1

2xdx

Пример 16. Исследовать на сходимость интеграл

I = ∫

−2 x2 -1

240

<<< < Предыдущая 12 13 14 15 16 17 18 19 20 21 22 2324 / 3624 25 26 27 28 29 30 31 32 33 34 35 36 > Следующая >>>

Соседние файлы в папке Высшая математика (РТФ)

#
18.05.20154.76 Mб33умк_Вакульчик_Элементы векторной алгебры.pdf
#
18.05.20155.38 Mб38умк_Вакульчик_Элементы линейной алгебры.pdf
#
18.05.20151.33 Mб40умк_Мальцев_Осн дискретной матем.pdf
#
18.05.20153.75 Mб39умк_Пальчик_Теория вероятностей.pdf
#
18.05.20155.68 Mб32умк_Цывис_Диф.уравнения_Ряды.pdf
#
18.05.20154.7 Mб39умк_Цывис_Функции_Интеграл. исчисл..pdf
#
18.05.20153.54 Mб76умк_Яско_ Диф.уравнения_Ряды.pdf