Если в плоскости Oxy точка опишет замкнутую линию L, ограни- чивающую область D, тогда в плоскости Ouv соответствующая точка опишет замкнутую линию L′ , ограничивающую область D′ , при этом ка- ждой точке P D будет соответствовать точка P′Î D′ . Таким образом, формулы замены переменных (1) взаимнооднозначно отображают область
D на область |
D′ .Так как, в общем случае, прямым линиям |
u = const , |
v = const на плоскости |
Ouv будут соответствовать кривые на плоскости |
Oxy, поэтому координаты u и v точки P называют криволинейными. |
|
|
Область |
D′ |
прямыми |
u = const , |
v = const |
разбиваем на прямо- |
угольные площадки со сторонами |
u |
и |
|
v (рис. 1), площадь элементар- |
ной фигуры |
P′P ′P ′P ′ |
DS ′ = Du × Dv . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
3 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Площадь соответствующей ей элементарной фигуры P P P P на |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
3 |
4 |
плоскости Oxy обозначим через |
S (при этом |
DS ′ ¹ DS , вообще говоря). |
Находим величину |
S |
как площадь криволинейного четырехугольника |
P P P P , координаты вершин которого |
|
|
|
|
|
|
|
|
|
|
1 |
2 |
3 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P (x , y ) |
|
x = x(u,v) |
|
|
|
|
y = y(u,v) |
|
|
|
|
|
|
|
1 |
1 |
1 |
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
P2 (x2 , y2 ) |
|
x2 = x(u + Du,v) |
|
|
|
y2 = y(u + Du,v) |
|
|
|
|
|
|
P3 (x3 , y3 ) |
|
x3 = x(u + Du,v + Dv) |
y3 = y(u + Du,v + Dv) . |
|
|
(2) |
|
|
|
P4 (x4 , y4 ) |
|
x4 = x(u,v + Dv) |
|
|
y4 = y(u,v + Dv) |
|
|
|
|
|
При |
вычислении |
площади |
криволинейного |
четырехугольника |
P P P P будем считать, |
что линии |
P P , |
P P , |
P P , P P – попарно парал- |
1 |
2 |
3 |
4 |
|
|
|
|
|
|
1 |
2 |
2 |
3 |
3 |
4 |
4 |
1 |
|
|
|
лельные прямые, а приращение функции будем заменять соответствующи- ми дифференциалами (или применять формулу Тейлора), тем самым будем пренебрегать бесконечно малыми более высокого порядка по сравнению с бесконечно малыми u и v . Тогда формулы (2) будут иметь вид
= ϕ(u,v)
= j(u,v) + |
¶j × Du |
|
|
¶u |
¶j × Dv |
= j(u,v) + |
¶j × Du + |
|
¶u |
¶v |
= j(u,v) + |
¶j × Dv |
|
|
¶v |
|
= ψ(u,v)
= y(u,v) + |
¶y × Du |
|
|
|
¶u |
¶y × Dv |
|
= y(u,v) + |
¶y × Du + |
(3) |
|
¶u |
¶v |
|
= y(u,v) + |
¶y × Dv |
|
|
|
¶v |
|
|

v |
|
|
|
y |
u + |
u |
|
|
|
|
|
|
u |
|
|
|
|
|
|
|
|
|
P3 |
v + |
v |
P′ |
P |
′ |
P4 |
P |
P2 |
|
|
|
|
|
2 |
3 |
|
|
|
v |
|
P′ |
|
|
|
P |
|
|
|
P′ |
P ′ |
|
|
1 |
|
|
|
|
D |
|
|
|
|
1 |
4 |
D′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
u + |
x |
|
|
|
0 |
|
u |
u |
|
|
x |
|
|
|
|
0 |
|
|
|
|
Рис. 1 |
|
Рис. 2 |
|
|
При сделанных допущениях криволинейный четырехугольник рас- сматриваем как параллелограмм, площадь которого равна удвоенной пло-
щади треугольника P P P и находится (по формуле из аналитической
1 2 3
геометрии)
|
|
|
|
|
|
DS = |
|
(x3 - x1 )( y3 - y2 ) - (x3 - x2 )( y3 - y1 ) |
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
¶j |
Du + |
¶j |
Dv |
|
× |
¶y |
Dv - |
|
|
|
¶j |
Dv |
|
|
¶y |
|
|
|
|
|
|
¶y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¶u |
¶v |
|
¶v |
|
|
|
¶v |
|
|
Du + |
¶v |
Dv = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¶u |
|
|
|
|
|
|
|
|
|
= |
|
¶j × |
¶y Du × Dv - ¶j × |
¶y Du × Dv |
|
|
= |
|
|
¶j × |
¶y - ¶j × ¶y |
|
× Du × Dv = |
|
|
|
|
|
|
|
¶u |
¶v |
|
|
|
|
|
|
¶v |
¶u |
|
|
|
|
|
|
|
|
|
|
|
|
|
¶u |
¶v |
|
|
¶v |
¶u |
|
|
|
|
|
|
|
|
|
|
|
|
¶j |
¶j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
¶u ¶v |
|
× Du × Dv = |
|
I |
|
× Du × Dv = |
|
I |
|
× DS ¢, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¶y |
¶y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¶u |
¶v |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
т.е. имеем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
× DS ′ , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
DS » |
|
I |
|
|
|
|
|
|
|
|
|
|
|
|
(4) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где определитель I |
называют функциональным определителем для функ- |
ций ϕ(u,v) и ψ(u,v) |
или якобианом. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Заметим, что равенство |
|
(4) является приближенным, так как при вы- |
числении площади |
|
|
S мы пренебрегали бесконечно малыми высшего по- |
рядка. Но чем меньше будут размеры площадок |
S |
и |
|
|
|
S ′ , тем равенство |
(4) будет точнее, а в пределе при |
S → 0 ( S ′ → 0 ) |
это равенство станет |
совершенно точным, т.е.
|
|
|
|
|
I = |
lim |
|
S |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S →0 |
DS ¢ |
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
S ′→0) |
|
|
|
|
|
|
|
|
|
|
|
|
|
Применим полученное равенство к вычислению двойного интеграла. |
Имеем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
∑ f (Pi¢) × |
|
|
|
× DS ¢ = |
|
∫∫ f (x, y)dxdy = |
lim |
∑ f (Pi ) × DSi |
= lim |
|
I |
|
|
|
|
|
|
|
|
n |
→∞ |
|
|
|
|
n →∞ |
|
|
|
|
|
|
|
|
D |
max |
S →0i =1 |
|
|
max S ′→0 |
|
|
|
|
|
|
|
|
= ∫∫ F (u,v) |
I |
dudv |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∫∫ f (x, y)dxdy = ∫∫ F (u,v) × |
|
I |
|
dudv |
(5) |
|
|
|
|
|
|
|
|
|
|
D |
|
|
|
D′ |
|
|
|
|
|
|
|
|
|
|
Формула (5) – |
формула замены переменных в двойном интеграле. |
Она впервые была получена русским математиком М. В. Остроградским. Суть формулы (5) замены переменных в двойном интеграле состоит
в следующем: интеграл, стоящий в правой части равенства «проще» как по виду функции, так и по области интегрирования.
Пример 1. Вычислить интеграл ID = ∫∫(2x - y)dxdy ,
D
D : x + y = 1, x + y = 2, 2x − y = 1, 2x − y = 3 .
Решение. Построить область D
y
|
|
|
|
|
|
|
2x – |
y = 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2x – y = 3 |
|
|
|
|
|
|
B |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D |
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
х |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Р |
|
|
|
|
|
x + y = 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x + y = 1 |
Вычисление данного интеграла I D по области D сведется к вычисле-
нию трех двойных интегралов. Для упрощения работы, связанной с вычисле- нием данного интеграла перейдем к новым переменным следующим образом
x + y = u
- =
2x y v
323
Тогда прямые x + y = 1 и x + y = 2 в системе координат Oxy преоб-
разуются в прямые u = 1 |
и u = 2 в системе координат Ouv, а прямые 2x |
– y = 1 и 2x – y = 3 в прямые v = 1 |
и v = 3. Параллелограмм D преобра- |
зуется в прямоугольник |
D1 со сторонами, |
параллельными координатным |
осям v и u. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
v |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
D1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x + y = u |
относительно u и v, получим |
Решая систему уравнений |
2x − y = v |
|
|
|
x = |
u + v |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
y = |
2u - v |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
Вычислим якобиан данного преобразования |
|
|
|
|
|
1 |
|
2 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I (u,v) = |
|
3 |
3 |
= - |
. |
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
- |
|
|
|
3 |
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
Так как |
I (u,v) ¹ 0 , |
то выбранное преобразование области D в об- |
ласть |
D1 взаимнооднозначно, а функция |
|
|
f (x, y) = 2x - y , как функция от |
u и |
v F (u,v) = 2 × |
u + v |
- |
2u − v |
= |
2 |
u + |
2 |
v - |
2 |
u + |
2 |
|
= v , |
непрерывна вме- |
|
|
|
|
|
|
|
|
|
|
|
3 |
|
3 |
3 |
3 |
|
3 |
|
3 |
|
|
|
|
|
|
сте со своими частными производными в области |
D1 . |
|
|
|
|
|
Следовательно, имеем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
1 |
2 |
3 |
|
4 |
|
|
∫∫(2x - y)dxdy = ∫∫ v × |
I |
dudv = ∫∫ |
vdvdu = |
∫du∫vdv = |
. |
|
|
|
|
|
|
|
|
3 |
3 |
3 |
|
D |
|
|
|
|
|
D |
|
|
|
|
D |
|
|
|
1 |
1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Итак ID |
= |
4 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

§ 5. Двойной интеграл в полярных координатах
Пусть требуется вычислить двойной интеграл
ID = ∫∫ f (x, y)dxdy |
(1) |
D |
|
с помощью перехода к полярной системе координат: сделаем замену пере- менных по формулам перехода от прямоугольной системы координат к полярной x = r cos ϕ, y = r sin ϕ .
В этом случае подынтегральная функция будет зависеть от r и ϕ : f (x, y) = f (r cos ϕ, r sin ϕ) = f (r,ϕ) .
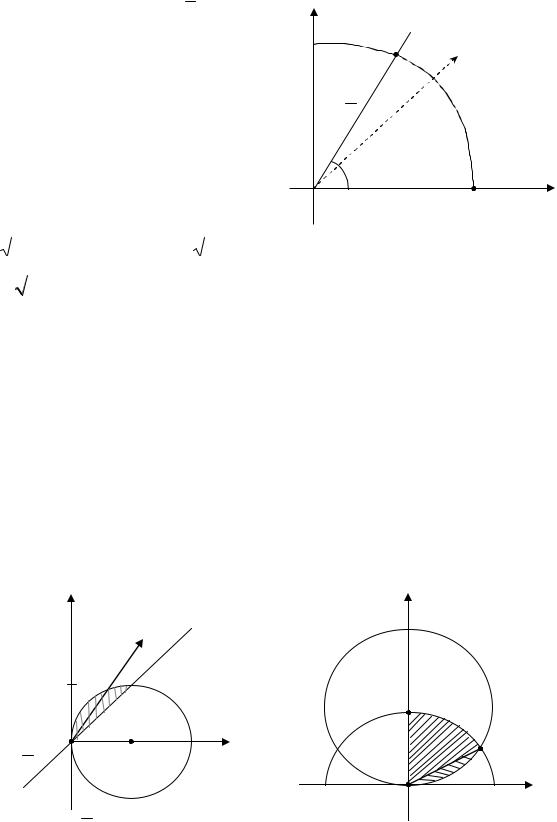
Если область D такова, что любой луч, выходящий из начала коор- динат и проходящий через внутреннюю точку области, пересекает границу
D не более, чем в двух точках, то такую область ( r = r1(ϕ), r = r2 (ϕ) , где |
r1(ϕ) ≤ r2 (ϕ), α ≤ ϕ ≤ β ) |
называют правильной применительно к полярной |
системе координат. Если D об- |
|
ласть правильная применительно к |
|
полярной системе координат, то |
y |
вычисление двойного |
интеграла |
|
сводится к вычислению повторно- |
|
B |
го интеграла по переменным r |
и |
|
|
K |
ϕ . Для расстановки пределов ин- |
|
r = r (ϕ) |
|
|
|
1 |
тегрирования из полюса проводят |
β |
r = r2 (ϕ) |
ограничивающие лучи ϕ = α |
и |
A |
ϕ = β , определяют уравнения вхо- |
|
α |
|
да в область (АМВ) – r = r1 (ϕ) и |
|
0 |
x |
|
|
|
выхода из нее (АКВ) – |
r = r2 (ϕ) . |
|
Рис. 1 |
|
|
α ≤ ϕ ≤ β, r1(ϕ) ≤ r ≤ r2 (ϕ) |
|
|
Тогда |
|
|
|
(рис. 1). |
|
|
|
|
|
Обычно внешний интеграл вычисляется по переменной |
ϕ , а внут- |
ренний – |
по r. |
|
|
|
|
В силу изложенного выше имеет место следующая формула вычис- |
ления двойного интеграла в полярных координатах |
|
|
|
β |
r |
(ϕ) |
|
|
∫∫ f (x, y)dxdy = ∫ dϕ |
2 |
∫ f (r cos ϕ, r sin ϕ)rdr , |
(2) |
|
D |
α |
r (ϕ) |
|
|
|
|
1 |
|
|
так как

I |
|
= |
|
|
D(x, y) |
|
|
= |
|
|
|
x = r cos ϕ |
|
|
|
= |
|
|
|
cos ϕ |
−r sin ϕ |
|
= |
|
r cos2 ϕ + r sin2 ϕ |
|
= |
|
r |
|
= r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D(r,ϕ) |
|
|
|
|
|
|
y = r sin ϕ |
|
|
|
|
|
|
|
sin ϕ |
r cos ϕ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Отметим, что если кривая r = r1 (ϕ) превращается в точку (полюс) (рис. 2), тогда r1 (ϕ) = 0 и формула (2) запишется в виде
|
β |
r (ϕ) |
|
|
∫∫ f (x, y)dxdy = ∫ du |
∫ |
f (r cos ϕ, r sin ϕ)rdr . |
(3) |
D |
α |
0 |
|
|
Если область D охватывает начало координат и любой полярный ра- |
диус пересекает ее границу в одной точке (рис. 3), тогда |
|
|
2π |
r (ϕ) |
|
|
∫∫ f (x, y)dxdy = ∫ dϕ ∫ |
f (r cos ϕ, r sin ϕ)rdr , |
(4) |
D |
0 |
0 |
|
|
где r = r(ϕ) – полярное уравнение кривой, ограничивающей область D.
Переход в двойном интеграле к полярным координатам удобно ис- пользовать в тех случаях, когда подынтегральная функция содержит сумму x2 + y2 , а граница области D содержит дуги окружностей и лучи, выхо-
дящие из начала координат.
r = r(ϕ)
D |
|
r = r(ϕ) |
|
|
|
D |
|
β |
0 |
P |
α |
|
|
0 |
P |
|
Рис. 2 |
|
Рис. 3 |
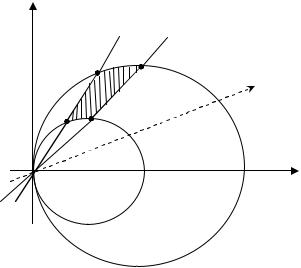
Пример 1. В двойном интеграле |
I D = ∫∫ f (x, y)dxdy перейти к по- |
|
|
|
|
|
D |
лярным координатам, если область |
D |
ограничена линиями: x2 + y 2 = 1, |
x2 + y 2 = 25 , y = 0, y = |
|
x , x ³ 0 . |
|
|
3 |
|
|
Решение. Уравнение |
x2 + y 2 = 1 – |
окружность с центром в точке O(0;0) |
радиуса 1. Уравнение |
x2 + y 2 = 25 |
также определяет окружность с цен- |
тром в точке O(0;0) радиуса 5.
Уравнения y = 0 и y = 
 3x явля-
3x явля-
ются уравнениями прямых. Учиты- вая условие x ³ 0 , получим об- ласть D (рис. 4).
Уравнение окружностей в полярных координатах имеют вид
|
|
|
|
r =1 |
(x2 + y 2 =1) |
|
|
|
|
и |
r = 5 |
(x2 + y2 = 25) . |
|
Тангенс угла наклона прямой |
y = |
|
|
|
|
|
|
|
3x |
к оси Ox равен |
|
3 , т.е. |
tgϕ = |
|
|
|
, j = π ; прямой |
|
|
|
3 |
y = 0 со- |
|
|
|
|
|
3 |
|
|
|
ответствует угол ϕ = 0 . Тогда имеем
π
35
∫∫f (x, y)dxdy = ∫ dj∫ f (r cos j, r sin j)rdr .
|
D |
0 |
1 |
|
Пример 2. В двойном интеграле |
ID = ∫∫ f (x, y)dxdy расставить пределы |
|
|
|
|
D |
|
интегрирования, если: |
|
|
|
|
1. |
D ограничена линиями: x2 |
+ y2 |
£ 4x, |
y ³ x ; |
2. |
D ограничена линиями: x2 |
+ y2 |
£ R2 , |
x2 + y2 - 2Ry £ 0, x ³ 0 . |
2
|
|
D |
D2 |
ϕ = π |
|
|
2 |
4 x |
A |
4 |
|
|
D1 |
|
ϕ = π |
0 |
x |
|
|
|
|
2 |
|
|
Решение. 1. Уравнение |
x2 + y2 = 4x |
или |
(x − 2)2 + y2 = 4 в полярных |
координатах имеет вид |
r = 4cos ϕ , прямая |
y = x дает j = π . Тогда об- |
|
|
|
|
4 |
ласть D имеет вид (рис. 5). |
|
|
|
|
π |
4 cos ϕ |
|
|
|
2 |
|
|
∫∫ f (x, y)dxdy = ∫ d j |
∫ |
f (r cos j, r sin j)rdr . |
D |
π |
0 |
|
|
|
4 |
|
|
|
2. Строим область интегрирования и записываем соответствующий интеграл.
Имея уравнения границ области
x2 + y2 = R2 , x2 + ( y - R)2 = R2 , x = 0, x ³ 0 ,
получим область D, изображенную на рис. 6. Для этой области D ϕ меня-
ется от 0 до π . Чтобы установить границы изменения радиуса, будем про- 2
водить лучи из начала координат и получим, что луч входит в область D
при r = 0, а точка выхода луча лежит или на окружности x2 + y2 - 2Ry = 0 ,
или на окружности x2 + y2 = R2 (в зависимости от угла наклона луча к оси
Ox). Поэтому область D |
разбиваем отрезком ОА на две области D1 и |
D2 . Запишем уравнение |
окружности в |
полярной |
системе координат |
x2 + y2 = 2Ry r = 2R sin ϕ |
и x2 + y2 = R2 , |
получим |
r = R. Тогда поляр- |
ные координаты точки А (точки пересечения окружностей) – это решение |
системы
r = 2R sin j |
|
|
|
A = p |
, R |
r = R |
6 |
|
Для области D угол меняется от 0 до |
π , а для области D2 – от |
π |
1 |
6 |
6 |
|
до π . Проводя луч, пересекающий область |
D , получим, что он входит в |
2 |
1 |
|
|
|
область при r = 0 , а выходит – при r = 2R sin ϕ . Для области D2 луч, про-
веденный из полюса, входит в эту область при r = 0 и выходит – при r = R.
Следовательно
|
π |
2R sin ϕ |
π |
|
|
6 |
2 |
R |
∫∫ f (x, y)dxdy = ∫ dϕ |
∫ |
f (r cos ϕ, r sin ϕ)rdr + ∫ dϕ∫ f (r cos ϕ, r sin ϕ)rdr . |
D |
0 |
0 |
π |
0 |
|
|
|
6 |
|
|
Пример 3. Вычислить двойной интеграл ID = ∫∫ |
1 − x2 |
− y |
2 |
dxdy , |
|
|
|
|
|
|
1 + x2 |
+ y |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D |
|
|
где D – |
верхний полукруг x2 + y2 ≤ 1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение. Перейдем к полярной системе координат |
x = r cos ϕ, y = r sin ϕ . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тогда |
x2 + y2 = r2 , а |
|
1 − x2 − y2 |
= |
1 − r |
2 |
|
; I = r . |
|
|
|
|
|
|
|
1 + x2 + y2 |
1 |
+ r |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тогда искомый интеграл будет иметь вид (рис. 7) |
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 − r |
2 |
|
|
|
|
1 |
1 − r2 |
|
|
|
|
|
|
|
|
|
ID = ∫∫ |
|
|
|
rddrdϕ = ∫dϕ∫ |
|
|
|
rdr = π(π − 2) . |
|
|
|
|
1 + r |
2 |
1 + r2 |
|
|
|
|
D |
|
|
0 |
|
0 |
|
|
|
|
|
|
|
y
Рис. 7
|
Пример 4. Вычислить двойной интеграл I D = ∫∫ |
|
dxdy |
, |
|
(x |
2 |
+ y 2 )2 |
|
D |
|
|
где область D ограничена окружностями x2 + y 2 = 4x, |
x |
2 |
+ y 2 = 8x и пря- |
|
мыми y = x и y = 2x. |
|
|
|
|
|
Решение. Область D имеет вид (рис. 8) |
|
|
|
|
|
Перейдем к полярным координатам x = r cos ϕ, |
y = r sin ϕ . Тогда по- |
дынтегральная функция будет равна f (x, y) = r−4 . Криволинейные участки границы области задаются уравнениями:
r2 cos2 ϕ + r 2 sin2 ϕ = 4r cos ϕ |
или |
r = 4cos ϕ |
r2 cos2 ϕ + r2 sin2 ϕ = 8r cos ϕ |
или |
r = 8cos ϕ , |
а прямолинейные участки уравнениями:
r sin ϕ = r cos ϕ или tgϕ = 1, откуда ϕ = π 4
r sin ϕ = 2r cos ϕ или tgϕ = 2 , откуда ϕ = arctg2 .
y
y = 2x
y = x
x2 + y2 = 8x
x2 + y2 = 4x
Рис. 8 |
|
|
Таким образом, угол ϕ изменяется в постоянных пределах от |
π |
до |
|
4 |
|
arctg2 . Для определения пределов изменения r пересекаем область |
D лу- |
чом, исходящим из полюса. При входе в область r = 4cos ϕ , а выход из об-
ласти r = 8cos ϕ . Значит |
r = 4cos ϕ – |
нижний предел интегрирования, а |
r = 8cos ϕ – |
верхний предел интегрирования, якобиан I = r . Тогда |
|
|
arctg2 |
8 cos ϕ |
r−4rdr = |
3 |
|
|
|
I = |
∫ |
dϕ ∫ |
. |
|
|
|
|
|
|
π |
4 cos ϕ |
128 |
|
|
|
|
4 |
|
|
|
|
|
Пример 5. При какой замене переменных область D, |
ограниченная |
линиями |
xy = 1, xy = 2, x − y + 1 = 0, x − y − 1 = 0 (x > 0, y > 0) |
перейдет в |
прямоугольник D1 , стороны которого параллельны координатным осям.