Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Пензенский Государственный Университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

умк_Цывис_Функции_Интеграл. исчисл

..pdf

Скачиваний:

Добавлен:

18.05.2015

Размер:

4.7 Mб

Скачать

☆

<<< < Предыдущая 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 2829 / 3629 30 31 32 33 34 35 36 > Следующая >>>

Sц = Sш + Sк ,

где Sц , Sш и Sк – соответственно площади кругов, получающихся при

пересечении цилиндра, шара и конуса плоскостью (MN). Это соотношение выполняется для любых сечений цилиндра, шара и конуса, лежащих в од- ной и той же горизонтальной плоскости. В силу принципа поперечных се- чений перейдем от соотношения

Sц = Sш + Sк

для площадей к такому же соотношению для объемов

Vц = Vш + Vк .

8.6. Объем тела вращения

Важным применением формулы объема тела по площадям попереч- ного сечения

V = ∫S (x)dx

является формула нахождения объема тела вращения вокруг оси.

Пусть криволинейная трапеция ограничена дугой L, перпендикуля- рами, опущенными из концов этой дуги на ось Ox, и отрезком [ab] , за-

ключенным между основаниями перпендикуляров, вращается вокруг Ox, то полученное при этом тело называется телом вращения с осью Ox и об- разующей L (рис. 1).

y
L	y = f(x)
a	b	x
О

Рис. 1

281

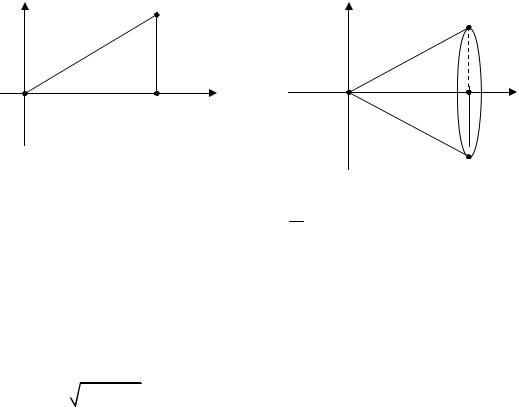
Получим формулу для объемов тел вращения вокруг осей координат. Сечениями, перпендикулярными к оси вращения, будут круги; поэтому, если знаем закон изменения радиусов этих кругов, то получим искомый объем, используя форму объема по площадям поперечного сечения.

Пусть ось вращения Ox, а уравнение образующей y = f(x). Тогда площадь сечения равна πy2 , и объем тела, ограниченного двумя сечения-

ми x = a и x = b, равен

V = π∫( f (x))2 dx .

При вычислении объема тела вращения вокруг оси Oy пишут урав- нение кривой, выражая x через y, т.е. x = ϕ( y) . Тогда искомый объем те-

ла вращения вокруг оси Oy равен

V = π∫ x2dy = π∫(ϕ( y))2 dy .

		α	α
Пример 32. Вычислить объем конуса и шара.
Решение. 1)	пусть конус имеет радиус основания R и высоту					h. Конус
получается при вращении		OAB вокруг оси Ox.
y	A		y
			y =	R	x
			y =		x
				n
					n	x
О	B		x
					R

Уравнение образующей конуса y = R x , а пределы интегрирования – h

от 0 до h, тогда искомый объем

πR2 h

πR2 x3

πR2 h

V = π∫

dx =

∫ x2dx =

;

2) пусть данный шар радиуса R, а уравнение вращающейся полуок- ружности y = R2 − x2 .

282

y	y

y = R 2 − x 2

О R

Тогда

							R	(R2 - x2 )dx =	4	pR3 .
					V = p × ∫				4
					V = p × ∫
							− R	3
							− R
Пример 33. Вычислить объем
тела, полученного вращением части											y
OB параболы	y2 = 2 px					вокруг оси					y
Oy.											B
Решение. Уравнение параболы,								раз-			B
решенное относительно					x	имеет вид					y0
решенное относительно					x	имеет вид
	x =		y2	.							y 2 = 2 px
	x =			.							y 2 = 2 px
		2 p
Тогда искомый объем											x
											x
y0	y4				py5
V = p ∫			dy =			0	.
V = p ∫	4 p2		dy =		20 p2		.
0	4 p2				20 p2

Пример 34. Вычислить объем тора.

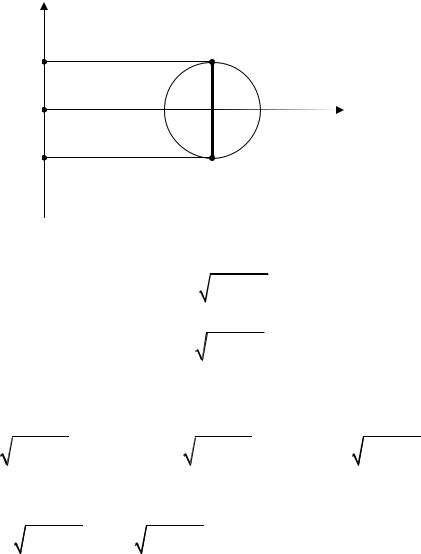
Решение. Тором называется тело, получающееся при вращении круга радиу- са r вокруг оси, лежащей в его плоскости на расстоянии b (b > r) от центра.

Если круг вращается вокруг прямой CD, тогда объем тора есть раз- ность объемов вращения криволинейных трапеций CMKND и CMLND вокруг оси Oy.

Найдем уравнение кривых в виде x = ϕ( y) . Пусть начало координат находится в точке O, тогда уравнение окружности LMNK имеет вид

(x - b)2 + y2 = r2 ,

тогда

x = b ± 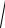r2 - y2 .

283

y
C		M
	r
O	L	K	x
		(b,0)
D		N

Уравнение кривой MKN будет

x = j, ( y) = b + r2 - y2 ,

а уравнение кривой MLN

x = j2 ( y) = b - r2 - y2 .

Пределы интегрирования в промежутке

[-r;r ] , тогда объем тора

можно вычислить по формуле

V = p ∫ (b + r 2 - y2 )2 dy - p ∫ (b - r2 - y2 )2 dy = 4pb ∫ r2 - y2 dy

−r

Неопределенный интеграл

dy =

r 2

arcsin

+ C .

∫

r 2 - y2

r2 - y2

Сделаем подстановку для

y Î[-r;r] получим, что искомый объем

тора V = 2p2br2 .

Объем тела вращения для кривой, заданной в параметрической форме

Пусть уравнение вращающейся кривой задано в параметрической форме

x = ϕ(t); y = ψ(t)

считаем при этом, что функция x = ϕ(t) определяет t как однозначную функцию от x: t = φ(x) .

Тогда искомый объем тела вращения вокруг оси Ox

b	x = j(t); y = y(t)	t2	× j¢(t)dt .

V = p∫ y2dx =		= p ∫ (y(t))2
a	j(t1 ) = a;j(t2 ) = b	t1

284

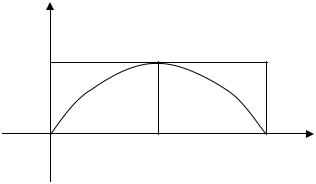
Отметим, что если			y = ψ(t) определяет		t	как однозначную функ-
цию от y, то объем тела вращения вокруг оси Oy
β			x = ϕ(t); y = ψ(t)		t2		′

V = π∫ x	2	dy =		= π ∫ [		2
			ψ(t1 ) = α;ψ(t2 ) = β			ϕ(t)]	ψ (t)dt .
α					t1

Пример 35. Вычислить объем тел, образованных вращением фигуры ОВАО вокруг оси Oy и вокруг оси ВС для циклоиды

x = a(t − sin t); y = a(1 − cos t), t [0;2π] .

Решение. Построим искомую фигуру, определяющую тело вращения

D B E

При вращении вокруг оси Oy получаем объем

2a	2a	2a
Vy = π ∫ (x22 − x12 )dy = π ∫ x22 dy − π ∫ x12 dy ,
0	0	0
где x = x1 ( y) – уравнение кривой ВА;	x = x2 ( y)	– уравнение кривой ОВ.

При подстановке y = a(1 − cost) , следует иметь ввиду, что для первого ин-

теграла t меняется от 2π до π, для второго – от 0 до π. Тогда имеем

π π

Vy = π ∫ a2 (t − sin t)2 a sin tdt − π∫a2 (t − sin t)2 sin tdt =

2π 0

= πa3 ∫ (t − sin t)2 sin tdt = 6π3a3.

2π

Для вычисления объема тела, получающегося при вращении вокруг оси ВС, перенесем начало координат в точку С, тогда в новых координа- тах уравнения имеют вид

x′ = a(t − π − sin t); y′ = a(1 − cos t) .

285

Учитывая лишь дугу ВА, получим

	2a		π
V = π ∫ (x′)2 dy′ = πa3 ∫ (t − π − sin t)2 sin tdt =
0			2π
0				πa3
=	t − π = z	= −πa3 ∫	(z + sin z)2 sin zdz =	πa3
=	t − π = z	= −πa3 ∫	(z + sin z)2 sin zdz =	(9π2 − 16).
		π		6
				6

Пример 36. Вычислить объем тела, образованного вращением во- круг полярной оси фигуры, ограниченной этой осью и дугой логарифмиче-

ской спирали r = eϕ , ϕ[0; π] .

Решение. Запишем данное уравнение в параметрической форме

					ϕ	cos ϕ
			x = r cos ϕ = e			cos ϕ
				= r sin ϕ = eϕ sin ϕ

			y
Тогда имеем			y2 = e2ϕ sin2 ϕ; dx = eϕ (cos ϕ − sin ϕ)d ϕ , откуда
b			π				π
V = π∫ y2dx = π∫e3ϕ sin2 ϕ(cos ϕ − sin ϕ)dϕ = = −							π	(e3π − 1) .
V = π∫ y2dx = π∫e3ϕ sin2 ϕ(cos ϕ − sin ϕ)dϕ = = −								(e3π − 1) .
a			0			15
a			0
Значение V получили отрицательное, так как значению ϕ = 0 соот-
ветствует точка (1;0) , а значению ϕ = π –						точка N (−eπ ,0) , лежащая левее
точки М.
Итак, V =	π	(e3π − 1) .
Итак, V =		(e3π − 1) .
15
	8.7. Площадь поверхности вращения
Пусть на отрезке [ab]				y = f(x) имеет непрерывную производную.

Рассмотрим поверхность, образуемую вращением дуги АВ вокруг оси Ox, уравнение этой дуги задается в виде y = f(x). Площадь поверхности, описан- ной дугой некоторой кривой, определим как предел площадей тех поверхно- стей, которые образованы вращением вписанных в дугу ломанных (хорд) при условии, что наибольшее звено этих ломанных стремится к нулю.


Отрезок	[ab] разбиваем точками				x0 , x1,..., xn	на отрезки длины
x0 , x1,..., xn ,	восстанавливаем ординаты				y0 , y1,..., yn	в точках деления.
		(i =		) . Когда кривая вращается вокруг оси Ox,
Строим хорды	Mi −1Mi	(i =	1, n	) . Когда кривая вращается вокруг оси Ox,
каждая из хорд Mi −1Mi		описывает боковую поверхность усеченного ко-

286

нуса. Искомая поверхность тела вращения – сумма боковых поверхностей этих усеченных конусов:

	n		yi −1 + yi
	P = ∑	2p		×	c k	.


	n	2			i i
	i =1	2		y			Ki	Mi
y	Mi			y			Ki	Mi
y = f (x)	Mi −1				Mi −1			yi
	B				Mi −1			yi
	B						xi
A							xi
			x					x
О a x0 x1	xi −1 xi				x		c	x
					i −1		i	i

Тогда

yi −1 + yi

(Dx )2

+ (Dy )2

P = lim

∑2p

n →∞

(max x

→0) i =1

1 + ( f ¢(x))2 × Dxi

1 + ( f ¢(x))2 dx.

lim

∑2py(x)

=2p∫ f (x) ×

n→∞

i =1

(max xi →0)

Таким образом, площадь поверхности вращения определяется по формуле

P = 2p∫ y 1 + ( y¢)2 dx .

Пример 37. Найти площадь поверхности вращения дуги кубической параболы a2 y = x3 между точками x = 0 и x = a вокруг оси Ox.

3x2

Решение. Так как y¢ =

, тогда 1 + ( y¢)2

a4 + 9x4 .

Имеем

P =

a4 + 9x4 x3dx = pa

-1) .

∫

(10

287

Пример 38. Найти площадь поверхности вращения вокруг оси Ox

	2	2		2
		+ y		= a		.
астроиды	x 3	+ y	3	= a	3	.
							2		2	3		1
										2
										2	; y¢ = -	y 3
Решение.	Здесь имеем y = a 3							- x 3				y 3		.
Решение.	Здесь имеем y = a 3							- x 3						.
													1
												x3
												x3

Отметим, что дуга ВА дает только половину искомой поверхности.

A x

Тогда имеем

								1
							2
a	3	2							2
						y 3

P = 2 × 2p∫ a 2		- x 3	×	1	+

					x
0

					3
	1	a	2	2			−	1
						2			12	pa2 .

dx = 4pa 3 ∫ a 3				- x 3			x 3 dx =

							5
		0

Если вращающаяся кривая задана параметрически	уравнениями:
x = ϕ(t), y = ψ(t) , и при этом считаем, что производные x′	и y′ сущест-

вуют и непрерывны, а для функции существует обратная, тогда

P = 2p ∫ y (x¢)2 + ( y¢)2 dt .

Если вращающаяся кривая задана в полярных координатах уравне- нием ρ = f (ϕ) и ρ′ существует и непрерывна, то

ϕ2
ϕ2	rsin j × r2	+ (r¢)2 d j.
P = 2p ∫	rsin j × r2	+ (r¢)2 d j.
ϕ1

Пример 39. Вычислить площадь поверхности, полученной вращени- ем эллипса вокруг большой его оси.

288

Решение. Считаем, что эллипс задан в параметрической форме

	x = a cos ϕ; y = bsin ϕ .
Тогда x′ = −a sin ϕ;	y′ = b cos ϕ .

		k =	a2	− b2
Обозначим через k –	эксцентриситет эллипса				.
Обозначим через k –	эксцентриситет эллипса				.

При вращении эллипса вокруг большой оси получим полную по- верхность эллипсоида. Надо удвоить поверхность, полученную от враще- ния дуги четверти периметра эллипса, соответствующей изменению пара-

метра ϕ от 0 до

π . Тогда

P =

4π∫bsin ϕ

a2 sin2

ϕ + b2 cos2 ϕdϕ =

= −4πb ∫ a2 (1

− cos2 (ϕ) + b2 cos2 ϕ`d cos ϕ =

4πab

= −4πab ∫

1 − k 2 cos2 ϕd cos ϕ =

t = k cos ϕ

= −

∫

1 − t 2 dt =

arcsin k

∫ 1 − t 2 dt =

arcsin t

1 − t

2πab

1 − k 2

Следовательно, имеем

arcsin k

P = 2πab

1 − k

8.9. Приложение определенных интегралов

квопросам физики, механики и техники

1.Вычисление давления жидкости. Работа.

Пример 40. Вычислить силу давления воды на вертикальную тре- угольную пластину, имеющую основание b и высоту h, погруженную в воду так, что ее вершина лежит на поверхности воды.

289

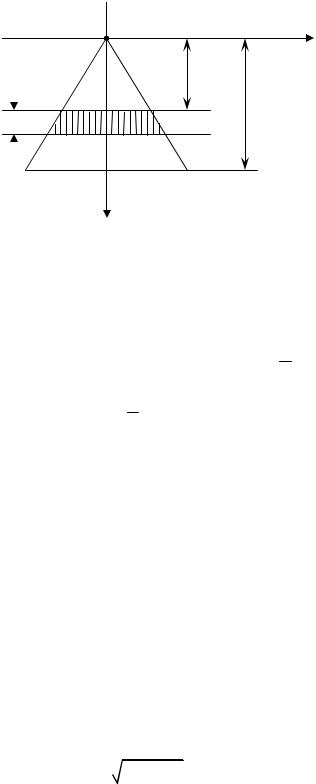
Решение. Выберем систему координат следующим образом

	B	y
		x
M	N	h

A C

Рассмотрим горизонтальную полоску, находящуюся на произволь- ной глубине x и имеющую толщину x ≈ dx . Применяя эту полоску в ка- честве прямоугольника, находим дифференциал площади dS = MNdx . Из

подобия треугольников DBMN и DABC имеем MN = b x , тогда h

dS = b x × dx h

Сила давления воды на эту полоску dP = x × dS (с учетом удельного веса воды 1).

Тогда сила давления воды на всю пластину АВС равна

h	b	h	b
P = ∫ xdS =		∫ x2dx =		h2 .
	h		3
0		0

Пример 41. Найти величину давления на полукруг, вертикально по- груженный в жидкость, если его радиус равен R, а диаметр его лежит на свободной поверхности жидкости (удельный вес жидкости равен γ).

Решение. Разобьем площадь полукруга на элементы – полоски, параллель- ные поверхности воды.

Площадь одного такого элемента, находящегося на расстоянии x от по- верхности, равна

dS = 2R2 - x2 dx .

Сила давления жидкости на элементарную полоску равна

dP = gx × dS

290

<<< < Предыдущая 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 2829 / 3629 30 31 32 33 34 35 36 > Следующая >>>

Соседние файлы в папке Высшая математика (РТФ)

#
18.05.20154.76 Mб34умк_Вакульчик_Элементы векторной алгебры.pdf
#
18.05.20155.38 Mб39умк_Вакульчик_Элементы линейной алгебры.pdf
#
18.05.20151.33 Mб42умк_Мальцев_Осн дискретной матем.pdf
#
18.05.20153.75 Mб40умк_Пальчик_Теория вероятностей.pdf
#
18.05.20155.68 Mб33умк_Цывис_Диф.уравнения_Ряды.pdf
#
18.05.20154.7 Mб40умк_Цывис_Функции_Интеграл. исчисл..pdf
#
18.05.20153.54 Mб77умк_Яско_ Диф.уравнения_Ряды.pdf