
14-es / Высшая математика (РТФ) / умк_Цывис_Функции_Интеграл. исчисл
..pdf
Используя определение линии уровня, получим: |
|
||||||||||||||||||||||||||||
а) |
xy = c – семейство гипербол; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
б) |
уравнение z = x + y задает поверхность, а линии уровня – |
прямые |
|||||||||||||||||||||||||||
x + y = c , параллельные прямой x + y = 0 ; |
|
|
|
||||||||||||||||||||||||||
в) поверхность, задаваемая уравнением – |
параболоид вращения: ли- |
||||||||||||||||||||||||||||
нии уровня – множество концентрических окружностей x2 + y2 = c |
с цен- |
||||||||||||||||||||||||||||
тром в начале координат; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
г) |
поверхность – |
гиперболический параболоид: линии уровня – рав- |
|||||||||||||||||||||||||||
носторонние гиперболы; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
д) поверхность – |
конус 2-го порядка: линии уровня – равносторонние |
||||||||||||||||||||||||||||
гиперболы xy = c2 ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
е) поверхность – |
параболический цилиндр, образующие которого па- |
||||||||||||||||||||||||||||
раллельны прямой x + y + 1 = 0 ; линии уровня – |
параллельные прямые. |
||||||||||||||||||||||||||||
3. Найти лини (поверхности) уровня следующих функций: |
|
||||||||||||||||||||||||||||
а) |
z = ln(x2 + y) ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
б) z = arcsin xy ; |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
в) z = f ( x2 + y2 ) ; |
|
|
|
|
|
|
|
|
|
|
|
|
г) u = x + y + z ; |
|
|||||||||||||||
д) u = x2 + y2 + z2 ; |
|
|
|
|
|
|
|
|
|
|
|
|
д) u = x2 + y2 − z2 . |
|
|||||||||||||||
Ответы: а) параболы |
y = C − x2 , |
|
|
C > 0 ; |
|
|
|
||||||||||||||||||||||
б) |
гиперболы xy = C |
( |
|
C |
|
£1) ; |
|
|
|
|
|
в) окружности x2 + y2 = C2 ; |
|||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||
г) |
плоскости, параллельные плоскости x + y + z = 0 ; |
|
|||||||||||||||||||||||||||
д) |
концентрические сферы с центром в начале координат; |
|
|||||||||||||||||||||||||||
е) при n > 0 однополостные гиперболоиды вращения вокруг оси OZ; |
|||||||||||||||||||||||||||||
при n < 0 двуполостные гиперболоиды вращения вокруг оси OZ; |
оба се- |
||||||||||||||||||||||||||||
мейства поверхностей разделяет конус |
|
x2 + y2 + z2 = 0 . |
|
||||||||||||||||||||||||||
4. Выразить объем конуса V |
как функцию ее |
|
|||||||||||||||||||||||||||
образующей x и радиуса основания y. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
Решение. Объем конуса V = |
1 |
S |
|
|
|
× h , |
|
|
|
||||||||||||||||||||
|
осн |
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
h |
|
x |
|||||||
где h – |
высота конуса; h = |
|
|
x2 - y2 . |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Тогда V = |
py2 × |
|
|
x2 - y2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
g |
|||
Область определения полученной функции – |
это |
|
|||||||||||||||||||||||||||
множество точек (xy) Î R2 , таких, что |
|
x |
|
³ |
|
y |
|
. |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||
91

5. Выразить объем конуса как функцию его полной поверхности S и длины образующей l.
Ответ: V (S,l) = |
|
S 2 |
× |
|
l 2 - |
S 2 |
; |
0 < S < p × l 2 . |
|||||||
3p2l |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
p2l2 |
|
|||||
6. Выразить объем конуса как функцию от углового осевого сечения |
|||||||||||||||
конуса |
α и от радиуса |
r |
шара, вписанного в конус. |
||||||||||||
|
|
|
|
p × r |
3 |
|
|
|
|
a 3 |
|
||||
|
|
|
|
|
1 + sin |
|
|
||||||||
Ответ: V (a, r) = |
|
|
|
|
|
|
|
|
2 |
|
|||||
|
|
|
|
|
|
|
. |
|
|||||||
|
3sin |
a |
cos |
2 a |
|
||||||||||
|
|
|
|
|
|
2 |
|
2 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
18.3. Предел функции нескольких переменных |
|||||||||||||
1. |
|
Вычислить |
предел |
|
и |
повторные пределы функции |
|||||||||
f (x, y) = |
xy |
|
|
|
|
|
|
|
|
|
|
||||
|
в точке О(0,0). |
|
|
|
|
|
|||||||||
x2 + y2 |
|
|
|
|
|
||||||||||
Решение. Пусть произвольная точка плоскости M(x,y) стремится к точке О(0,0) по прямой y = kx , которая проходит через точку О(0,0). То-
гда имеем
lim |
|
|
xy |
|
= lim |
|
|
kx2 |
= lim |
|
k |
|
= |
|
k |
|
. |
|
2 |
+ y |
2 |
|
2 |
+ k 2 x |
|
+ k |
2 |
|
+ k |
2 |
|||||
x®0 x |
x®0 x |
x®0 1 |
1 |
|
|||||||||||||
y®0 |
( y =kx) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
При различных значениях k (т.е. приближаясь к точке О(0,0) по различным прямым) получим различные значения искомого предела (при
k = 1 получим |
1 |
; при k = 2 получим |
2 |
). |
|
5 |
|||
2 |
|
|
||
Следовательно, предел данной функции в точке О(0,0) не существует. Вычислим повторные пределы функции в точке О(0,0). Имеем
|
|
|
|
|
|
xy |
|
|
|
|
lim lim f (x, y) = lim lim |
|
|
|
|
|
|
|
= lim 0 = 0 |
||
|
|
|
+ y2 |
|||||||
x®0 y®0 |
x®0 y®0 x2 |
|
x®0 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xy |
|
|
|
|
lim lim f (x, y) = lim |
|
|
|
|
|
|
|
= lim 0 = 0 |
||
lim |
|
|
|
|
|
|
|
|||
|
x |
2 |
+ y |
2 |
|
|||||
y®0 x®0 |
y®0 |
|
|
|
|
|
|
y®0 |
||
|
|
x®0 |
|
|
|
|
|
|
|
|
|
|
y -фиксир.( y ¹0) |
|
|||||||
92
Отметим, что из существования и равенства повторных пределов функции в данной точке не следует существование предела функции в этой точке.
2. Вычислить предел и повторные пределы функции:
а) f (x, y) = |
x2 |
− y |
2 |
|
в точке О(0,0); |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
x2 |
+ y |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
б) f (x, y) = |
x2 |
+ xy + y2 |
|
в точке О(0,0). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
x2 |
− xy + y2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Ответ: а) f (x, y) |
|
|
в точке |
О(0,0) |
|
предела не имеет; повторные пре- |
|||||||||||||||||||||||||||||||||||||
делы lim lim f (x, y) = 1; |
|
|
lim lim f (x, y) = −1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
x→0 y→0 |
|
|
|
|
|
y |
→0 x→0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
б) f (x, y) в точке О(0,0) предела не имеет |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
lim lim f (x, y) = lim lim f (x, y) = 1. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
x→0 y→0 |
|
|
|
y→0 x→0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
3. Вычислить повторные пределы функции |
|
|
|
|
f (x, y) = |
4x + 1 |
|
в точке |
|||||||||||||||||||||||||||||||||||
|
|
|
2x −1 |
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
О(0,0). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4x + 1 |
|
|
|
|
|
|
|
|
|
|
|
|
4 + |
|
|
y |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
||||||||||||
Имеем lim lim f (x, y) = lim |
lim |
|
|
= lim lim |
|
|
|
|
|
|
|
|
= 2 . |
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
||||||||||||||||||||||||||||||
x→0 y→0 |
|
|
|
x→0 |
y→0 2x −1 |
|
|
x→0 |
|
y→0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 − x |
|
|
|
|
|
|
|
|
|
|
|||||||||
Таким же образом устанавливаем, что |
lim lim |
4x + 1 |
= −1. |
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y→0 x→0 2x −1 |
|
|
|
|
|
||||||||||||||||||||||
4. Найти пределы функции |
f (x, y) в точке: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
а) f (x, y) = |
|
x2 y |
|
в точке О(0,0); |
|
|
б) |
|
f (x, y) = |
|
|
|
|
|
x |
|
|
в точке О(0,0). |
|||||||||||||||||||||||||
x |
4 + y |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x + y |
|
|
|
|
|
|||||||||||
Ответ: пределы не существуют. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
5. Найти предел функции |
|
f (x, y) = |
|
x4 |
+ y |
2 |
|
|
|
при |
|
|
|
x → ∞ и y → ∞ . |
|||||||||||||||||||||||||||||
|
|
x2 |
+ y |
4 |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Решение. Пусть |
x = t, y = t4 . Тогда |
при |
|
t → ∞ имеем |
x → ∞ и |
||||||||||||||||||||||||||||||||||||||
y → ∞ , а следовательно, lim f (t,t4 ) = lim |
t4 + t |
8 |
|
|
= lim |
t 2 |
+ t6 |
|
= 0 . |
|
|
||||||||||||||||||||||||||||||||
|
+ t16 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
t →∞ |
|
t →∞ t4 |
|
|
|
t →∞ 1 + t14 |
|
|
|
|
|
||||||||||||||||||||||||||
Если же x = t2 , y = t , тогда |
lim |
f (t2 ,t) = lim |
t8 |
+ t |
2 |
|
= lim |
t6 + 1 |
= ∞ . |
||||||||||||||||||||||||||||||||||
|
|
+ t4 |
|
|
2t 2 |
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
t →∞ |
|
|
|
|
t →∞ t 4 |
|
|
|
t →∞ |
|
|
|
|
|
|
|||||||||||||||||||||
Полученные различные пределы показывают, что предела не существует.
93

6. Вычислить пределы: |
а) lim |
1 + x2 y |
2 −1 |
; |
||
x2 + y2 |
|
|||||
|
x→0 |
|
||||
|
y→0 |
|
|
|
|
|
б) |
lim |
sin(x4 y |
2 ) |
; |
||
|
2 |
+ y2 )2 |
||||
|
x→0 (x |
|
||||
|
y→0 |
|
|
|
|
|
в) lim |
(x2 |
+ y2 )x2 y |
2 |
. |
|
|
− cos(x2 + y |
2 ) |
|||
x→0 1 |
|
||||
y→0 |
|
|
|
|
|
Ответ: а), б), в) |
– 0. |
|
|
|
|
|||
7. Вычислить предел функции |
f (x, y) и повторные пределы: |
|||||||
а) |
f (x) = log x (x + y) в точке M(1:0); |
|
|
|
||||
б) |
f (x) = |
sin x + sin y |
в точке M(0;0). |
|
|
|||
|
|
|
||||||
|
|
x + y |
|
|
|
|
|
|
Ответ: а) предел не существует |
|
|
) |
|
||||
|
|
|
|
|
lim |
lim f (x, y) |
= ∞ ; |
|
|
|
lim lim |
f (x, y) = 1; |
|||||
|
|
x→1 y→0 |
|
|
y→0 |
(x→1 |
|
|
б) |
lim f (x, y) = lim ( lim f (x, y)) = lim (lim f (x, y)) = 1. |
|||||
|
x→0 |
x→0 y→0 |
|
|
y→0 x→0 |
|
|
y→0 |
|
|
|
|
|
|
18.4. Непрерывность функции нескольких переменных |
|||||
1. Исследовать на непрерывность функцию |
||||||
|
|
x2 |
- y2 |
, (x, y) ¹ (0,0) |
||
|
|
|
|
|
|
|
|
|
|
|
+ y2 |
||
|
|
f (x, y) = x |
2 |
|
||
|
|
|
|
(x, y) = (0,0) |
||
|
|
0, |
||||
Решение. Для всех точек |
(x, y) Î R2 , кроме точки (0,0) функция |
|||||
f (x, y) |
непрерывна – как частное непрерывных функций (многочленов), |
|||||
причем знаменатель отличен от нуля при (x, y) ¹ (0,0) . Для исследования
на непрерывность данной функции в точке |
(x, y) = (0,0) |
необходимо ис- |
|||||
следовать существование предела |
lim f (x, y) . Если предположить, что |
||||||
|
|
|
|
|
( x, y)→(0,0) |
|
|
этот предел существует, то будем иметь |
|
|
|||||
|
lim f (x,0) = lim f (0, y) . |
|
|||||
|
x→0 |
|
|
y→0 |
|
|
|
Но последнее равенство для данной функции не выполняется, так как |
|||||||
|
|
x |
2 |
|
|
- y2 |
|
lim f (x,0) = lim |
|
|
=1, а |
lim f (0, y) = lim |
= -1. |
||
|
|
||||||
x→0 |
x→0 x |
2 |
|
y→0 |
y→0 y2 |
|
|
94
Таким образом, |
lim f (x, y) |
не существует. Значит точка (0,0) – точ- |
||||||
|
|
( x, y)→(0,0) |
|
|
|
|
|
|
ка разрыва функции |
f (x, y) . |
|
|
|
|
|
||
2. Исследовать на непрерывность функцию |
f (x, y) |
отдельно по пе- |
||||||
ременным x и |
y и по совокупности переменных |
x и |
y |
в точках О(0,0), |
||||
|
|
1, |
xy = 0 |
|
|
|
|
|
М(0,1), В(1,0), |
если |
|
|
|
|
|
|
|
f (x, y) = cos(x - y) - cos(x + y) |
|
¹ 0. |
||||||
|
|
|
|
|
|
, |
xy |
|
|
|
|
2xy |
|
||||
|
|
|
|
|
|
|
||
Решение. Данную функцию |
f (x, y) |
представим в виде (используя |
|||||||
формулу разности косинусов) |
|
|
|
|
|
|
|
||
|
1, |
xy = 0 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
f (x, y) = sin x ×sin y |
|
xy ¹ 0. |
||||||
|
|
|
|
|
|
|
, |
|
|
|
|
x × y |
|
||||||
|
|
|
|
|
|
||||
1) Так как lim f (x, y) = lim |
sin x |
× |
sin y |
=1 = f (0,0) , то f (x, y) не- |
|||||
|
|
||||||||
x→0 |
x→0 |
x |
y |
|
|
||||
y→0 |
y→0 |
|
|
|
|
|
|
|
|
прерывна в точке О(0,0) и, следовательно, непрерывна в этой точке по от- дельным переменным x и y.
2) Рассмотрим функцию f (0, y) . Тогда из определения функции f (x, y)
имеем, что |
f (0, y) = 1 для всех |
y, и, следовательно, эта функция непре- |
|||||||
рывна в точке |
y = 1. А это означает, |
что f (x, y) непрерывна в точке |
|||||||
M (0,1) по переменой y. |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
sin x |
×sin1, x ¹ 0 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|||
Рассмотрим функцию |
f (x,1) = |
|
|||||||
|
|
|
|
|
|
|
x = 0 |
||
|
|
|
|
|
|
1, |
|||
Так |
как |
lim f (x,1) = lim |
sin x |
×sin1 = sin1 ¹ 1 = f (0,1) , то функция |
|||||
|
|||||||||
|
|
y→0 |
y→0 |
x |
|
|
|||
f (x,1) не является непрерывной по переменой x в точке M (0,1) . Отсюда имеем, что f (x, y) не является непрерывной в точке M (0,1) по совокупно-
сти переменных |
x и y, так как в противном случае в силу теоремы |
4 она |
|
была бы непрерывной по переменой x. |
|
|
|
3) Рассуждая аналогично пункту 2 относительно точки |
В(1,0) |
уста- |
|
навливаем, что |
f (x, y) непрерывна в точке В по переменой |
x, и не явля- |
|
ется непрерывной как по переменой y, так и по совокупности переменных x и y.
95
3. Найти точки разрыва функций:
а) |
f (x, y) = |
|
|
|
|
2x |
|
|
; |
|
|
|
|
|
|
|
|
б) |
f (x, y) = ln(9 - x2 - y2 ) ; |
|||||||||||
|
x2 |
+ y |
2 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
в) f (x, y) = |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
; |
|
|
г) |
f (x, y) = sin |
y |
; |
|
|
|
|
|
||||
|
x2 |
+ y2 - z2 |
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|||||||||||||||
д) |
f (x, y) = |
sin x × cos y |
; |
|
|
|
е) |
f (x, y) = tg(x2 + y2 + z2 ) . |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
xy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Ответы: а) О(0,0); |
|
|
б) точки окружности |
x2 + y2 = 92 ; в) точки ко- |
||||||||||||||||||||||||||
нической поверхности |
x2 + y2 = z2 ; |
г) все точки прямой |
x = 0 ; д) все точ- |
|||||||||||||||||||||||||||
ки прямых x = 0 и y = 0 ; е) все точки сфер x2 + y2 = z2 = p + pk, |
k = 0,1, 2... |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
4. Исследовать функции на непрерывность по переменным x |
и |
y, и |
||||||||||||||||||||||||||||
по совокупности переменных x и y: |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
x2 y |
2 |
|
|
|
, x4 + y4 ¹ 0 |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
а) |
f (x, y) = |
|
|
|
4 + y4 |
|
и М(1,2); |
|
|
|
|
|||||||||||||||||||
x |
|
|
|
|
|
|
|
|
в точках О(0,0) |
|
|
|
|
|||||||||||||||||
|
|
|
|
x4 + y4 = 0 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
0, |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
x2 y2 |
|
|
, x4 + y4 ¹ 0 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−4 |
|
|
−5 |
|
||||||||||||
б) |
|
|
4 |
+ y |
4 |
О(0,0) |
и |
M (10 |
,10 |
) ; |
||||||||||||||||||||
f (x, y) = x |
|
|
|
|
|
|
|
|
|
|
в точках |
|
|
|||||||||||||||||
|
|
0, x4 + y4 = 0 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
0, x - y = 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
в) |
f (x, y) = |
|
|
|
- cos y |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
cos x |
- y |
¹ 0 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, x |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
x |
- y |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
p |
p |
, M 2 (p, p) . |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
в точках О(0,0), M1 |
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
4 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Ответы: а) в точке |
|
|
О(0,0) |
f (x, y) непрерывная по |
x, непрерывная |
|||||||||||||||||||||||||
по y и разрывная по совокупности переменных x и y; |
б) в точках О и М |
|||||||||||||||||||||||||||||
функция непрерывна по отдельным переменным и по совокупности пере- менных; в) в точках О и M 2 функция непрерывна по отдельным пере-
менным и по совокупности переменных, а в точке M1 функция разрывная по отдельным переменным и по совокупности переменных.
5. Доказать, что функция
|
|
xy |
, при x ¹ 0, y ¹ 0 |
|
|
|
|
|
|
|
2 |
+ y2 |
||
f (x, y) = x |
|
|||
0, |
при x = 0, y = 0 |
|||
96

имеет разрыв в точке (0,0), хотя и непрерывна в ней по каждой из пере- менных в отдельности.
6. Доказать, |
|
что если z = f (x, y) – |
непрерывная функция, то множе- |
|||||||||||||||||
ство точек М, где |
|
f (x, y) ≤ C , где |
C – |
заданное число, – замкнуто; если |
||||||||||||||||
f (x, y) < C , то множество точек М – |
открыто. |
|
|
|
|
|
|
|||||||||||||
7. Для функций u(x, y) |
найти частные производные в окрестности |
|||||||||||||||||||
точки О(0,0) и их непрерывность в точке О(0,0), если: |
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||
1) u = x2 + y2 ; |
2) u = x4 + y4 ; |
3) u = 3 |
|
; |
|
|||||||||||||||
xy |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||
4) u = 3 x2 y2 ; |
|
5) u = 4 x4 + y4 ; |
6) u = 3 x3 + y3 ; |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
7) u = 3 x4 + y4 . |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Ответы: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
1) |
частные производные |
u(x, y) |
существуют в окрестности точки |
|||||||||||||||||
О(0,0), за исключением самой точки О(0,0); |
|
|
|
|
|
|
||||||||||||||
2) частные производные функции |
u(x, y) |
существуют в окрестности |
||||||||||||||||||
точки О(0,0) и непрерывны в этой точке; |
|
|
|
|
|
|
|
|
||||||||||||
3) частная производная |
∂u |
существует в окрестности О(0,0), за ис- |
||||||||||||||||||
∂x |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂u |
|
|
|
|
|
ключением точек |
|
(0, y) |
y ¹ 0 ; частная производная |
∂y |
существует в ок- |
|||||||||||||||
рестности точки О(0,0), за исключением точек |
(x,0) |
x ¹ 0 ; частные про- |
||||||||||||||||||
изводные разрывны в точке О(0,0); |
|
|
|
|
|
|
|
|
|
|||||||||||
4) |
∂u |
|
существует в окрестности точки |
О(0,0), за исключением то- |
||||||||||||||||
∂x |
|
|||||||||||||||||||
чек (0, y) y ¹ 0 ; |
|
∂u |
существует в окрестности точки |
О(0,0)О, за исклю- |
||||||||||||||||
|
∂y |
|||||||||||||||||||
чением точек |
(x,0) |
x ¹ 0 ; частные производные разрывны в точке О(0,0); |
||||||||||||||||||
5) |
∂u |
и |
∂u |
существуют в окрестности точки О(0,0), кроме самой точки; |
||||||||||||||||
∂x |
∂y |
|||||||||||||||||||
6) |
∂u |
и |
∂u |
|
существуют в окрестности точки О(0,0), за исключени- |
|||||||||||||||
∂x |
∂y |
|
||||||||||||||||||
ем точек прямой |
y = -x |
(x ¹ 0) , они разрывны в точке О(0,0); |
||||||||||||||||||
7) |
∂u |
и |
∂u |
|
существуют в окрестности точки О(0,0) и непрерывны |
|||||||||||||||
∂x |
∂y |
|
||||||||||||||||||
в этой точке.
97

18.5. Дифференцирование функций нескольких переменных
1. Найти частные производные и полные дифференциалы первого
порядка от функции f (x, y) = arctg |
x |
|
в точке |
|
M0 (1;2) . |
|||||||||||||||||||
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Решение. Найдем частные производные и полный дифференциал |
||||||||||||||||||||||||
функции в произвольной точке |
|
M (x, y) |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
∂f (x, y) = |
|
1 |
|
|
|
|
|
× |
1 |
= |
|
|
|
y |
|
|
|
||||||
|
¶x |
|
|
|
|
|
|
x |
2 |
|
|
y |
|
x2 + y2 |
|
|
|
|||||||
|
|
|
|
1 + |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
¶f (x, y) |
= |
|
1 |
|
|
|
|
|
× |
|
-x |
= |
|
-x |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
¶y |
|
|
x |
|
2 |
|
|
|
2 + y |
|
|
||||||||||||
|
|
|
|
|
|
|
y3 x |
2 |
|
|||||||||||||||
|
|
1 |
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
¶f (x, y) = |
∂f (x, y) |
× dx + |
∂f (x, y) dy = |
y |
|
dx - |
|
x |
|
dy . |
|||||||
¶x |
x2 + y2 |
|
x2 |
+ y2 |
|||||||||||||
|
|
¶y |
|
|
|
|
|
||||||||||
Подставляя в полученные выражения |
x = 1 |
и y = 2 , |
получим |
||||||||||||||
∂f (M0 ) = |
2 |
; |
∂f (M 0 ) = - |
1 |
; ¶f (M 0 ) = |
2 |
dx - |
1 |
dy . |
|
|||||||
|
|
|
|||||||||||||||
|
|
|
5 |
|
|||||||||||||
¶x |
5 |
|
¶y |
5 |
|
|
5 |
|
|
|
|
|
|||||
При решении данной задачи мы сначала находили частные произ- водные функции, а потом ее полный дифференциал.
Но данную задачу во многих случаях можно решать следующим об- разом: сначала находят полный дифференциал, пользуясь правилами вы- числения дифференциала суммы, произведения, частного и элементарных функций, а потом собирают коэффициенты при dx и dy . Коэффициент
при dx – это |
∂f , а коэффициент при dy – |
|
∂f . |
||
|
¶x |
|
|
¶y |
|
2. Найти частные производные первого порядка функции |
|||||
|
z = sin |
x2 |
+ y |
2 |
. |
|
x3 |
+ y3 |
|||
|
|
|
|||
Решение. 1) По определению дифференциала имеем dz = d sin u = cosudu ,
где u = x2 + y2 ; x3 + y3
98
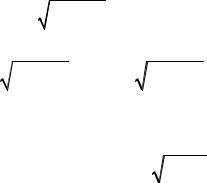
x2 |
+ y |
2 |
|
(x3 + y3 )d (x2 + y2 ) - (x2 + y |
2 )d (x3 + y3 ) |
|||||||||
2) du = d |
|
|
|
|
|
= |
|
|
|
|
|
|
|
; |
|
3 |
|
|
|
3 |
|
3 |
|
2 |
|
||||
|
x |
+ y |
3 |
|
(x |
+ y |
) |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|||||
3) d (x2 + y2 ) = 2xdx + 2 ydy ; d (x3 + y3 ) = 3x2dx + 3y3dy ;
4) |
Собирая коэффициенты при dx и |
dy |
получим |
|
|
||||||||||||||||||||||
dz = cos |
x2 + y2 |
× |
(-x4 - 3x2 y2 |
+ 2xy3 |
|
|
dx + cos |
|
x2 + y2 |
× |
(2x3 y - 3x2 y2 - y |
4 ) |
dy ; |
||||||||||||||
x3 + y3 |
(x3 + y3 )2 |
|
|
|
x3 + y3 |
|
|
|
(x3 + y3 )2 |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
5) |
Коэффициенты при |
|
dx и |
dy – |
это |
∂z |
и |
|
∂z |
соответственно; |
|||||||||||||||||
¶x |
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¶y |
|
|
||||||
3. Найти точки, где не существуют частные производные функции |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
z = |
|
|
x2 + y2 . |
|
|
|
|
|
|
|
|
|
|
|
|||||||
Решение. Имеем |
∂z = |
|
|
x |
|
|
; |
|
∂z |
= |
|
y |
|
|
|
. Но при x = 0 и |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
¶x |
|
|
x2 + y2 |
|
¶y |
|
|
x2 + y2 |
|
|
|||||||||||||
y = 0 эти формулы теряют смысл. Найдем частные производные функции
z в точке О(0,0). Имеем
|
|
|
|
|
|
( |
x)2 |
|
|
|
Dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
¶z(0,0) |
= lim |
f (0 + Dx,0) - f (0,0) |
= lim |
|
D |
|
= |
lim |
|
|
|
|
|
. |
|
|
|
|
|
|
||||||||||
|
¶x |
Dx |
|
|
|
|
|
|
|
|
|||||
|
x→0 |
x→0 |
Dx |
x→0 |
|
Dx |
|||||||||
Но этот предел не существует, а, следовательно, и |
∂z(0,0) |
не существует. |
|||||||||||||
|
|
|
|
|
|
|
¶x |
|
|
|
|
|
|
|
|
Аналогичным образом доказываем, что ∂z(0,0) не существует.
¶x
4. Найти частные производные функции:
а) z = x y (x > 0) ; |
u z |
y |
|
|
|
||||
б) u = |
|
|
|
|
> 0 |
|
; |
||
|
|
||||||||
|
|
x |
x |
|
|
|
|||
в) u = x y z |
; |
г) u = x y × y z × z x . |
|
|
|
||||
Решение:
а) при нахождении частной производной функции z = x y по переме- ной x, искомую функцию z рассматриваем как функцию одной переме- ной x, т.е. y считаем фиксированной переменной (параметром) или, дру- гими словами, y считаем постоянным числом.
Тогда, при фиксированном y функция z = x y является степенной
функцией от x. Тогда |
∂z = y × x y−1 . |
|
¶x |
99

Аналогично, при вычислении |
∂z |
считаем |
x – фиксированным зна- |
|
|||
|
¶y |
|
|
чением (постоянным), поэтому функцию z = x y |
рассматриваем как пока- |
||
зательную функцию аргумента y. |
|
|
|
Тогда получим |
∂z |
= x y ln x . |
|
||
|
¶y |
|
б) u¢ |
= |
|
y z −1 |
|
- |
|
|
|
|
|
|||
x |
|
|
|
|||
|
|
|
x |
|
|
|
y |
= - |
z |
y z |
||||
|
|
|
|
|
|
; |
|
x2 |
|
|
|||||
|
|
x |
x |
|
|||
z
u¢y = z × y ; u¢z y x
|
y z |
y |
|||
= |
|
|
ln |
|
; |
|
|
||||
|
x |
|
x |
||
в) u¢ |
= y z × x y z −1 ; u¢ = x y z × z × y z −1 × ln x ; u¢ = x y z ln xy2 × ln y ; |
||||
|
x |
|
y |
z |
|
г) u¢ |
= x y−1 |
× y z +1 × z x + x y y z z x ln z ; u¢ = x y ln xy z z x + x y y z −1 |
× z x+1 ; |
||
|
x |
|
|
y |
|
|
|
|
u¢ = x y × y z |
× ln y × z x + x y +1 × y z × z x−1 . |
|
|
|
|
z |
|
|
5. |
Доказать, что функция |
z = x y × y x удовлетворяет соотношению |
|||
|
|
|
x ∂z + y |
∂z = (x + y + ln z) × z . |
|
|
|
|
¶x |
¶y |
|
6. |
Доказать, что функция |
u = ln(ex + e y + ez ) удовлетворяет соотно- |
|||
шению |
∂u + ∂u + |
∂u =1. |
|
|
|
|
¶x |
¶y |
¶z |
|
|
7. |
Найти скорость изменения функции z = x3 + y2 в точке |
(1,1) в за- |
|||
висимости от изменения каждой из переменных x и y. |
|
||||
Ответ: скорость изменения по x равна 3, по y равна 2. |
|
||||
8. |
Найти частные производные и полные дифференциалы первого и |
||||
второго порядка функции: z = ϕ(u, υ) , где u = x2 + y2 , u = x × y .
Решение. Данную задачу решим двумя способами.
Первый способ:
1) Найдем частные производные и полный дифференциал первого порядка. Имеем
|
∂z = |
∂z |
× |
∂u + |
|
∂z |
|
× ∂υ = |
∂z |
× 2x + |
∂z |
|
× y |
|||||||||||
|
|
|
|
|
|
|
|
¶u |
||||||||||||||||
|
¶x |
¶u |
¶x |
¶u ¶x |
¶u |
|
|
|||||||||||||||||
|
|
∂z |
= |
|
|
∂z |
× |
∂u + |
|
|
∂z |
|
× ∂υ = |
∂z × 2 y + |
|
∂z |
x . |
|||||||
|
|
|
|
|
|
|
|
|
¶u |
|||||||||||||||
|
|
¶y |
|
¶u |
¶y |
|
¶u ¶y |
¶y |
|
|
|
|||||||||||||
Тогда dz = |
∂z dx + |
|
|
∂z |
dy = 2 |
|
∂z |
(xdx + ydy) + |
∂z |
( ydx + xdy) . |
||||||||||||||
|
|
|
|
|
||||||||||||||||||||
|
¶x |
|
|
¶y |
|
|
|
¶u |
|
|
¶u |
|
||||||||||||
100
