
14-es / Высшая математика (РТФ) / умк_Цывис_Функции_Интеграл. исчисл
..pdfПример 5. Доказать, что функция f (x, y) не является непрерывной
в точке О(0,0), но в данной точке существуют обе частные производные, равные между собой
|
|
2xy |
, x |
2 |
+ y2 |
¹ 0 |
|
|
|
|
|
||||
|
2 + y2 |
|
|||||
f (x, y) = x |
|
|
|
|
|||
|
|
x = y = 0. |
|
|
|||
0, |
|
|
|||||
Решение.
1. Функция f (x, y) не имеет предела при (x, y) → (0,0) (для дока-
зательства положим, например, y = kx ), а, следовательно, не является не-
прерывной в точке (0,0). |
|
|
|
||
2. С другой стороны имеем |
|
||||
∂f |
(0,0) = lim |
f ( |
x,0) − f (0,0) |
= 0; |
∂f (0,0) = 0 . |
¶x |
|
|
|||
x→0 |
Dx |
¶y |
|||
3. Получаем, что существование частных производных функции в точке не гарантирует даже непрерывности функции в этой точке.
Отметим, чтобы функция z = f (x, y) была дифференцируема в точке
M0 (x0 , y0 ) , на нее налагают условия более жесткие, чем существование ча-
стных производных.
Теорема 7. (достаточные условия дифференцируемости функции). Если функция z = f (x, y) имеет частные производные в некоторой окре-
стности точки M0 (x0 , y0 ) , непрерывные в самой точке, то она дифферен- цируема в точке M0 (x0 , y0 ) .
Доказательство. Полное приращение функции z = f (x, y) в точке
M0 (x0 , y0 ) представим в следующем виде
Df (x0 y0 ) = f (x0 + Dx, y0 + Dy) - f (x0 y0 ) =
=( f (x0 + Dx, y0 + Dy) - f (x0 , y0 + Dy)) + ( f (x0 , y0 + Dy) - f (x0 , y0 )) =
=fx¢(a, y0 + Dy) × Dx + f y¢(x0 ,b) × Dy.
Здесь применим теорему Лагранжа о конечных приращениях для со-
ответствующих разностей, где x0 < a < x0 + x, y0 < b < y0 + |
y . |
|
|
|||
По условию теоремы частные производные f |
′ |
(x, y) и |
f |
|
′ |
(x, y) не- |
|
x |
|
|
y |
|
|
прерывны в точке M0 (x0 , y0 ) , тогда справедливы равенства:
41

lim |
f |
′(a, y |
|
+ Dy) = f |
′ |
(x , y ), |
|
lim |
f |
′ |
(x ,b) = f |
|
′(x , y ). |
|||||||||
x |
→0 |
|
x |
|
|
0 |
|
|
|
|
x |
0 0 |
|
x→0 |
|
y |
0 |
|
|
y |
0 0 |
|
y |
→0 |
|
|
|
|
|
|
|
|
|
|
|
|
y→0 |
|
|
|
|
|
|
|
|
Из последних равенств, в силу связи между пределом функции и са- |
||||||||||||||||||||||
мой функцией будем иметь равенства: |
|
|
|
|
|
|
|
|
|
|
||||||||||||
f |
′(a, y |
0 |
+ Dy) = f |
′ |
(x , y ) + a , |
|
f |
′(x ,b) = f |
′ |
(x , y ) + b , |
||||||||||||
|
x |
|
|
|
|
|
|
x |
0 |
0 |
|
|
y |
0 |
|
|
y |
0 |
|
0 |
||
где α и |
β бесконечно малые функции при |
x → 0, |
|
y → 0 . |
||||||||||||||||||
Тогда полное приращение функции f (x, y) в точке M0 (x0 , y0 ) имеет вид |
||||||||||||||||||||||
|
Df (x , y ) = f |
′ |
(x y ) × Dx + f |
′ |
(x , y ) × Dy + a × x + b × Dy . |
|||||||||||||||||
|
|
|
|
0 0 |
|
x |
|
0 |
0 |
|
y |
0 |
0 |
|
|
|
|
|
|
|
||
А это означает, что функция z = f (x, y) |
дифференцируема в точке |
|||||||||||||||||||||
M0 (x0 , y0 ) . Что и требовалось доказать.
Отметим, что непрерывность частных производных в точке не явля- ется необходимым условием дифференцируемости функции в этой точке. Так функция
|
2 |
+ y2 )sin |
|
1 |
|
|
2 |
+ y2 |
¹ 0 |
(x |
|
|
|
, x |
|||||
|
|
|
|
|
|||||
|
|
|
|||||||
f (x, y) = |
|
|
|
x2 + y2 |
|
|
|
||
|
|
x = y = 0 |
|
|
|
|
|
|
|
0, |
|
|
|
|
|
|
|
||
дифференцируема в точке О(0, 0). Но при x2 + y2 ¹ 0 частная производная
∂f (x, y) = 2x sin |
|
1 |
|
- |
|
x |
|
× cos |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
¶x |
x2 + y2 |
|
|
|
x2 + y2 |
|
|
|
x2 + y2 |
|||
не имеет предела при (x, y) → (0,0) |
|
и, следовательно, не является непре- |
||||||||||
рывной функцией в точке О(0,0). Чтобы в этом убедиться, достаточно по- |
||||||||||||
казать, что ∂f (x,0) |
не имеет предела при x → 0 . |
|
|
|
|
|
|
|
|||||||||
¶x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Функции с непрерывными частными производными называются не- |
|||||||||||||||||
прерывно дифференцируемыми. |
Например, |
функция |
z = y2ex2 + y2 |
диффе- |
|||||||||||||
ренцируема в любой точке |
M (x, y) Î R2 так как ее частные производные |
||||||||||||||||
∂z |
2xy2 × ex |
2 |
+ y |
2 |
|
∂z |
|
2 |
+ y |
2 |
+ 2 y3ex |
2 |
+ y |
2 |
|
||
¶x = |
|
|
и |
|
= 2 yex |
|
|
|
|
|
|||||||
|
|
|
¶y |
|
|
|
|
|
|
|
|||||||
всюду непрерывны.
42
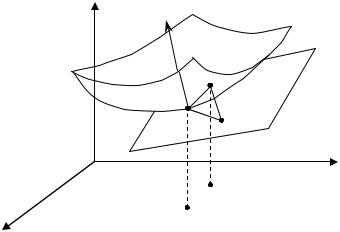
Понятие дифференцируемости для функций трех и более независи- мых переменных водится аналогично как для функции двух переменных.
Геометрический смысл дифференцируемости.
Для функций |
одной переменной |
|
y = f (x) , |
дифференцируемость |
||||||
функции в точке x0 , |
означает, |
что существует касательная к графику |
||||||||
функции в точке M (x0 , f (x0 )) . |
|
|
|
|
|
|
|
|||
Пусть |
задана |
непрерывная |
функция |
двух |
переменных |
|||||
z = f (x, y), |
(x, y) 0 . График этой функции представляет некоторую по- |
|||||||||
верхность S R3 . |
|
|
|
|
|
|
|
|
|
|
Пусть плоскость P проходит через точку N0 (x0, y0 , z0 ) |
поверхности |
|||||||||
S; N (x, y, f (x, y)) – |
произвольная точка на поверхности S; N1 – основание |
|||||||||
перпендикуляра, проведенного из точки N на плоскость P (рис. 1). |
||||||||||
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
||
|
|
|
|
|
|
|
|
S |
|
|
|
|
|
|
|
|
N |
|
P |
|
|
|
|
|
|
|
|
N0 |
|
N1 |
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
M(x,y) |
|
|
|
|
|
|
|
|
M1(x0 , y0 ) |
|
|
||
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 1 |
|
|
|
|
||
Плоскость P, |
проходящая через точку M 0 (x0 , y0 , z0 ) |
поверхности |
||||||||
S, называется касательной плоскостью к поверхности S в этой точке, если |
||||||||||
при N N0 |
(N S ) |
|
ρ (N , N1) |
|
|
|
||||
|
|
|
lim |
= 0 . |
|
|
||||
|
|
|
|
|
|
|
|
|||
|
|
|
M →M 0 |
ρ (N , N0 ) |
|
|
||||
Если функция z = f (x, y) дифференцируема в точке M 0 (x0 , y0 ) , то в |
||||||||||
точке N0 (x0 , y0 , z0 ) |
существует касательная плоскость к поверхности S |
|||||||||
(графику этой функции), причем уравнение касательной плоскости имеет вид
∂z (M |
|
)(x − x |
) + |
∂z (M )( y − y ) − (z − z ) = 0 , |
|||
∂x |
0 |
0 |
|
∂y |
0 |
0 |
0 |
|
|
|
|||||
43

|
|
|
¶z (M |
|
¶z |
|
|
|
|
а вектор |
n к касательной плоскости, т.е. |
n = |
0 ), |
(M |
0 ), |
-1 назы- |
|||
|
|||||||||
|
|
¶x |
|
¶y |
|
|
|||
вается |
вектором нормали (нормалью) |
к |
поверхности |
S |
в точке |
||||
N0 (x0 , y0 , z0 ) . |
|
|
|
|
|
|
|
||
Прямая, проходящая через точку N0 и параллельная вектору n на-
зывается нормалью к поверхности S в точке N0 уравнение которой имеет вид
|
x − x0 |
= |
y − y0 |
= |
z − z0 |
. |
|
- f x¢(x0 , y0 ) |
- f y¢(x0 , y0 ) |
|
|||
|
|
1 |
|
|||
Правило дифференцирования сложной функции. |
||||||
Пусть z = f (u,v) – функция двух переменных, каждая из которых |
||||||
является функцией независимых переменных x и y: u = u(x, y), v = v(x, y) .
Тогда z = f (u(x, y),v(x, y)) = F (x, y) – сложная функция двух независимых
переменных x и y, а переменные u и v – промежуточные аргументы. Имеет место следующая теорема (правило дифференцирования
сложной функции). |
|
|
|
|
Теорема 8. |
Если |
функция |
z = f (u,v) |
дифференцируема в точке |
M 0 (u0 ,v0 ) , а функции |
u = u(x, y), |
v = v(x, y) |
дифференцируемы в точке |
|
P0 (x0 , y0 ) D( f ) , |
то сложная функция z = f (u,v) , где u = u(x, y) и |
|||
v = v(x, y) , дифференцируема в точке P0 (x0 , y0 ) , причем ее частные произ-
водные находят по формулам:
∂z = |
∂z |
× |
∂u + |
∂z × |
∂v , |
(1) |
|
|
|
||||||
¶x |
¶u |
¶x |
¶v |
¶x |
|
||
∂z = |
∂z |
× |
∂u + |
∂z × |
∂v . |
(2) |
|
|
|||||||
¶y |
¶u |
¶y |
¶v |
¶y |
|
||
Доказательство. Докажем формулу (1). Так как функция |
z = f (u,v) |
||||||
дифференцируема в точке M 0 (u0 ,v0 ) , тогда ее полное приращение в этой точке имеет вид
Dz = |
∂z × Dxu + |
∂z |
× Dyv + a × Dxu + b × Dxv |
|
||||||||||||||||
|
|
|
||||||||||||||||||
|
|
¶x |
|
|
|
|
¶y |
|
|
|
|
|
|
|
|
|
|
|
||
Полученное равенство разделим на |
Dx ¹ 0 . |
|
|
|
|
|||||||||||||||
Dz |
= |
¶z |
× |
D |
u |
+ |
|
¶z |
× |
yv |
+ a × |
D |
|
u |
+ b |
D |
v |
|
||
|
|
x |
|
|
|
|
|
|
|
x |
|
x |
. |
(3) |
||||||
Dx |
¶x |
|
|
¶y |
Dx |
|
|
|||||||||||||
|
|
Dx |
|
|
|
|
Dx |
|
Dx |
|
||||||||||
44
|
Если |
x → 0 , то |
xu → 0 |
и |
xv → 0 |
в силу непрерывности функ- |
|||||||||||
ции |
u(x, y) |
и v(x, y) . |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
lim |
xu = |
∂u ; |
lim |
xv = |
∂v . |
|
|
||||
|
|
|
|
|
|
x→0 |
Dx |
¶x |
x →0 Dx |
¶x |
|
|
|
||||
|
|
|
|
|
1 |
a × Dxu = a |
x ; |
1 |
b × Dxv = b |
|
xv . |
|
|||||
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
Dx |
|
|
Dx |
Dx |
|
|
|
Dx |
|
|||
|
Переходя |
к |
пределу в |
равенстве |
(3) с |
учетом того, что |
|||||||||||
lim a × |
xu = 0, |
lim b × |
xv = 0 имеем |
∂z = |
∂z |
× |
∂u + ∂z × |
∂v . |
|||||||||
|
|||||||||||||||||
x→0 |
|
Dx |
|
x |
→0 |
Dx |
|
|
¶x |
¶u |
¶x |
|
¶v |
¶x |
|||
Аналогичным образом доказываем (2). Теорема доказана. Рассмотрим частные случаи задания сложной функции:
1. |
z = f (x, y), |
x = x(t) |
|
и |
y = y(t) , тогда ∂z = |
∂z × |
dx |
+ |
∂z |
× |
dy |
. |
|
|
||||||||||||||||
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¶t |
|
¶x |
|
dt |
¶y |
dt |
|
|
|
||||
2. |
z = f (x, y), |
y = y(x) , т.е. z = f (x, y(x)) – |
сложная функция одной |
|||||||||||||||||||||||||||
независимой переменой, тогда |
|
dz |
= ∂z × |
dx |
+ |
∂z × |
dy |
и |
|
∂z = |
∂z + |
∂z × |
dy |
– |
||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
dx |
¶x dx |
¶y dx |
|
|
¶x |
|
¶x |
|
¶y dx |
||||||||||||
формула полной производной. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Рассмотрим случай функции трех переменных. |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
1) Пусть ψ = f (u,v, w), u = u(x, y, z), v = v(x, y, z), |
|
w = w(x, y, z) . Тогда |
||||||||||||||||||||||||||||
|
|
|
∂F = |
∂F × |
∂u + |
∂F × |
∂v + |
∂F × |
∂w |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
¶x |
|
¶u |
|
¶x |
¶v |
|
|
¶x |
¶w |
¶x |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
∂F = |
∂F × |
∂u + |
∂F × |
∂v + |
∂F × |
∂w |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
¶y |
|
¶u |
¶y |
¶v |
|
|
¶y |
¶w |
¶y |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
∂F = |
∂F × |
∂u + |
∂F × |
∂v + |
∂F × |
∂w . |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
¶z |
¶u |
¶z |
¶v |
|
|
¶z |
¶w |
¶z |
|
|
|
|
|
|
|
|
|
|
|||||||||
2) Пусть |
z = f (x, y,u) , |
|
где |
|
|
y = y(x) |
|
и |
|
u = u(x) . |
Тогда |
|||||||||||||||||||
z = f (x, y(x),u(x)) = F (x) – |
функция одной переменой x. |
|
|
|
|
|
|
|
||||||||||||||||||||||
Тогда |
∂z = |
∂z × |
∂x + |
|
∂z |
× |
∂y + |
∂z |
× |
∂u |
или |
|
с |
учетом |
того, что |
|||||||||||||||
|
|
|
¶x |
|
||||||||||||||||||||||||||
|
|
¶x |
¶x |
¶x |
|
¶y |
¶x |
¶u |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
x = x, y = y(x), u = u(x) получим |
|
|
|
|
|
|
|
|||
|
dz |
= |
∂z + |
∂z × |
dy |
+ |
∂z |
× |
du |
. |
|
|
|
|
|
||||||
|
dx |
¶x |
¶y dx |
¶u dx |
||||||
Эту формулу называют формулой полной производной.
45

Замечание. Между частной ∂z |
и полной |
dz |
производными, входя- |
||||||||||||
|
|||||||||||||||
|
|
|
∂z + |
∂z × |
¶x |
∂z |
|
|
|
dx |
|||||
щими в формулу |
dz |
= |
dy |
+ |
× |
du |
имеется существенное разли- |
||||||||
|
|
|
|
||||||||||||
|
dx |
¶x |
¶y |
|
dx |
¶u dx |
|||||||||
чие. Полная производная |
dz |
– |
это обычная производная от z как функция |
||||||||||||
dx |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
∂z
x, а ¶x – частная производная от z по переменой x, входящей в выражение
функции непосредственно, т.е. при условии, что другие переменные (y и u), зависящие от х, при дифференцировании остаются постоянными.
Пример |
6. |
Найти |
|
производную функции |
u = x2 y3 z , где |
||||||||
x = t, y = t 2 , z = sin t . |
|
|
|
|
|
|
|
|
|||||
Решение. Так как |
u |
является функцией одной независимой переме- |
|||||||||||
ной t, то |
du |
= |
∂u × |
dx |
+ |
∂u × |
dy |
+ |
∂u × |
dz |
подставляя x, y |
и z получим |
|
|
|
|
|
||||||||||
|
dt |
¶x |
dt |
¶y |
|
dt |
¶z dt |
|
|||||
du = 2xy2 z ×1 + 3x2 y3 z × 2t + x2 y3 cost = t 7 (8sin t + t cost). dt
Пример 7. Найти частные производные функции z = f (x2 y, x y ) .
Решение. |
Данную функцию можно представить в виде z = f (u,v) , |
||||||||||||||||||||
где u = x2 y |
и |
|
v = x y . |
Таким образом, z |
является функцией двух пере- |
||||||||||||||||
менных u и v, а u и v |
являются функциями от двух переменных x и y. |
||||||||||||||||||||
Для нахождения частных производных |
|
∂z и |
∂z |
воспользуемся формулами: |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¶x |
¶y |
|
||
|
|
∂z = |
∂z |
× |
|
∂u + |
∂z × |
∂v = |
∂z |
|
× 2xy + |
∂z × y × x y −1 , |
|||||||||
|
|
|
|
|
|
||||||||||||||||
|
|
¶x |
|
¶u |
¶x |
¶v |
¶x |
¶u |
|
¶v |
|||||||||||
|
|
∂z = |
|
∂z |
× |
∂u + |
∂z × |
∂v = |
|
∂z |
× x |
2 + |
∂z × x y × ln x . |
||||||||
|
|
|
|
|
|||||||||||||||||
|
|
¶y |
|
¶u |
¶y |
¶v |
¶y |
|
¶u |
¶v |
|||||||||||
Пример 8. Доказать, что функция |
z = y × j(x2 - y2 ) удовлетворяет |
||||||||||||||||||||
соотношению |
|
1 |
× |
∂u + |
1 |
× ∂u = |
z |
. |
|
|
|
|
|
|
|||||||
|
|
y2 |
|
|
|
|
|
|
|||||||||||||
|
|
x |
¶x |
|
|
|
y |
¶y |
|
|
|
|
|
|
|
|
|||||
Решение. Найдем частные производные |
|
||||||||||||||||||||
∂z = y × j¢ × 2x = 2xy × j¢; |
∂z = j + y × j¢(-2 y) = j - 2 y2 × j¢. |
||||||||||||||||||||
¶x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¶y |
|
|
|
|
|
|
46
Подставляя их в левую часть соотношения, получим:
1 |
× 2x × y × j¢ + |
1 |
(j - 2 y2j¢) = 2 yj¢ + j - 2 yj¢ = j = |
y × j |
= |
z |
. |
|
x |
y |
|
|
|||||
|
y |
y y2 |
|
y2 |
||||
Что и требовалось доказать.
§9. Дифференциал функции нескольких переменных. Инвариантность формы первого дифференциала.
Правила дифференцирования
Важной частью исследования функций является локальное исследо- вание, под которым понимается сравнение значения функции в данной
точке со значениями функции в точках, близких к данной. |
|
||||||||||||||||||||
Если функция |
z = f (x, y) |
дифференцируема в точке M0 (x0 , y0 ) , то |
|||||||||||||||||||
ее полное приращение в этой точке можно представить в виде |
|
||||||||||||||||||||
Df (x , y |
|
) = f |
x |
′(x , y ) × Dx + f |
y |
′(x , y ) × Dy + a × Dx + b × Dy . |
(1) |
||||||||||||||
0 0 |
|
|
|
0 |
|
|
0 |
|
|
|
|
0 |
0 |
|
|
|
|
||||
Главная линейная часть полного приращения функции (z) относи- |
|||||||||||||||||||||
тельно аргументов ( |
x и |
y ) называется полным (первым) дифференциа- |
|||||||||||||||||||
лом функции (z)в точке M0 , обозначается |
|
|
|
|
|
||||||||||||||||
dz(M |
0 |
) = df (x , y |
0 |
) = f |
x |
′(x , y ) × Dx + f |
′(x , y ) × Dy . |
(2) |
|||||||||||||
|
|
|
|
|
0 |
|
|
|
|
0 |
0 |
|
y |
0 |
0 |
|
|||||
Приращения независимых |
|
x и |
|
|
y называют дифференциалами не- |
||||||||||||||||
зависимых переменных x и y и обозначают соответственно dx и dy. |
|
||||||||||||||||||||
Тогда полный дифференциал функций z = f (x, y) |
в точке M0 (x0 , y0 ) |
||||||||||||||||||||
записывают в виде |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
df (x , y ) = |
¶f (x0 , y0 ) |
dx + |
¶f (x0 , y0 ) × dy . |
(3) |
||||||||||||||||
|
|
||||||||||||||||||||
|
|
|
|
0 |
0 |
|
|
|
|
¶x |
|
|
|
|
¶y |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Выражения |
|
|
¶f (x0 , y0 ) |
dx, |
¶f (x0 , y0 ) dy называют частными диффе- |
||||||||||||||||
|
|
|
|||||||||||||||||||
|
|
|
|
¶x |
|
|
|
|
|
|
¶y |
|
|
|
|
|
|
||||
ренциалами функции |
z = f (x, y) |
и обозначают dx z |
и |
d y z . |
|
||||||||||||||||
Замечание. Равенство |
|
|
(2), приводящее к понятию дифференциала, |
||||||||||||||||||
позволяет говорить о дифференциале как о главной линейной части при-
ращения f функции f (x, y) . Действительно, |
∂f |
× Dx + |
∂f × Dy – часть пол- |
|
¶x |
|
¶y |
ного приращения f , линейно зависящая от |
x |
и |
y , называется глав- |
47
ной потому, что ее доля (вес) в полном приращении Df стремится к еди-
нице при α и b ® 0 в равенстве (2).
Пример 1. Найти по определению первый дифференциал функции
z = x2 + y 2 в точке M0 (1, 2) . |
|
Решение. Найдем полное приращение функции z в точке |
M0 (1;2) |
z = f ( x0 , y0 ) = f (x0 + x; y0 + y) − f (x0 , y0 ) ; |
|
Df (1, 2) = f (1 + Dx, 2 + Dy) - f (1, 2) = (1 + Dx)2 + (2 + Dy)2 - (12 + 22 ) = |
|
= (1 + Dx)2 -1 + (2 + Dy)2 - 22 = Dx × (2 + Dx) + Dy × (4 + Dy) = |
|
= 2 × Dx + (Dx)2 + 4Dy + (Dy)2 . |
|
То есть Df (1,2) = 2 × Dx + 4Dy + (Dx)2 + (Dy)2 . |
|
Главная линейная часть полного приращения функции |
z в точке |
M0 – это 2 × Dx + 4Dy , следовательно, полный (первый) дифференциал име-
ет вид dz = 2 × dx + 4 × dy . |
|
|
|
|
|
|
|
|
|
|
||||
Частные дифференциалы |
dx z = 2dx; |
d y z = 4dy . |
|
|||||||||||
Замечание. Определение первого (полного) дифференциала анало- |
||||||||||||||
гично обобщается на случай функции любого числа переменных. |
|
|||||||||||||
Инвариантность формы первого дифференциала |
|
|||||||||||||
Пусть |
z = f (x, y); x = x(u,v); y = y(u,v) , тогда по определению пер- |
|||||||||||||
вого дифференциала имеем |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
dz = |
∂f (x, y) |
|
dx + ∂f (x, y) dy . |
(1) |
|||||||
|
|
|
||||||||||||
|
|
|
|
|
¶x |
¶y |
|
|
|
|
||||
Рассмотрим функцию z(x(u,v), y(u,v)) как функцию переменных |
u |
|||||||||||||
и v. Считая, |
что u и v независимые переменные найдем дифференциал |
|||||||||||||
функции z. Согласно определению имеем |
|
|
|
|
|
|
||||||||
|
dz = |
¶f (x(u,v), y(u,v)) |
du + ¶f (x(u,v), y(u,v)) dv . |
(2) |
||||||||||
|
|
|
||||||||||||
|
|
|
¶u |
|
|
|
|
|
|
¶v |
|
|
|
|
Так как |
|
|
∂f (x(u,v), y(u,v)) |
= ∂f × |
∂x |
|
∂f × |
∂y |
|
|
||||
|
|
|
+ |
, |
|
|||||||||
|
|
|
¶v |
|
|
|
¶x |
¶u |
|
¶y |
¶u |
|
|
|
48
|
∂f (x(u,v), y(u,v)) |
= |
∂f × |
∂x |
+ ∂f × |
∂y |
, |
|||||||||||||
|
|
|
|
¶u |
|
|||||||||||||||
|
|
|
|
|
|
¶v |
|
|
|
¶x |
|
¶y |
|
¶u |
|
|||||
то формула (2) будет иметь вид |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
dz = ¶f × |
¶x |
+ |
¶f × |
¶y |
du + ¶f × |
¶x + |
¶f × |
¶y dv . |
||||||||||||
|
|
|||||||||||||||||||
¶x |
¶u |
¶y |
¶u |
|
¶x |
¶v |
¶y |
¶v |
||||||||||||
Перегруппировав слагаемые в (3), получим |
|
|
|
|
||||||||||||||||
|
|
¶f |
|
¶x |
|
¶x |
|
|
|
¶f |
¶y |
|
¶y |
|
||||||
dz = |
|
|
|
|
du + |
¶v |
dv |
+ |
|
|
|
|
du |
+ |
¶v |
dv . |
||||
|
|
|
|
|
|
|||||||||||||||
|
|
¶x |
¶u |
|
|
|
|
¶y ¶u |
|
|
||||||||||
Но для функций x(u,v), y(u,v) |
независимых переменных |
||||||
ференциалы имеют вид |
|
|
|
|
|
|
|
dx = |
∂x |
du + |
∂x dv; dy = |
∂y |
du + |
∂y dv . |
|
|
|
||||||
|
¶u |
¶v |
|
¶u |
¶v |
||
Тогда из соотношений (3) |
и (4) получаем |
|
|||||
|
|
dz = ∂f |
dx + ∂f |
dy . |
|
||
|
|
|
¶x |
¶y |
|
|
|
(3)
u, v диф-
(4)
(5)
В сопоставлении формул (5) и (2) и заключается свойство, назы-
ваемое инвариантностью формы первого дифференциала. Остановимся подробнее на этом.
Если z = f (x, y) , а x |
и y – независимые переменные, то |
|||
|
dz = |
|
∂f (x, y) |
dx + ∂f (x, y) dy . |
|
|
¶x |
||
|
|
|
¶y |
|
Если же |
x, y – переменные, зависящие от других (независимых) пе- |
|||
ременных u, v, |
то дифференциал |
dz сложной функции z(x(u,v), y(u,v)) |
||
равен правой части в формуле (2). В силу доказанного выше, правые части
формул (2) и (5) совпадают. Поэтому равенство |
dz = |
∂f |
dx + |
∂f dy спра- |
|
|
¶x |
|
¶y |
ведливо не только для независимых переменных |
x, y, но также и для тех, |
|||
которые являются функциями от других переменных (в рассматриваемом нами случае – от u, v).
Другими словами, свойство инвариантности первого дифференциала состоит в следующем: форма (структура) первого дифференциала (1) не меняется независимо от того, аргументы функции независимые перемен-
49
ные или являются функциями от других переменных, т.е. формальная за- пись дифференциала в обоих случаях одинакова.
Свойство инвариантности формы первого дифференциала позволяет установить следующие правила дифференцирования.
Пусть u и v – дифференцируемые функции каких-либо перемен- ных. Тогда имеет место теорема 9.
Теорема 9.
1) d (c ×u) = c × du, |
c - const ; |
2) d (u ± v) = du ± dv ; |
||||||||
|
|
|
|
|
|
u |
vdu - udv |
|
||
3) d (u,v) = udv + vdu ; |
4) d |
|
= |
|
, v ¹ 0 . |
|||||
v |
v2 |
|||||||||
Доказательство. (Докажем, например, формулу (3)). Рассмотрим |
||||||||||
функцию z = u × v двух переменных u |
и v. Дифференциал этой функции |
|||||||||
dz равен |
|
|
|
|
|
|
|
|
||
|
|
|
dz = |
∂z |
× du + |
∂z × dv . |
|
|
||
|
|
|
|
|
|
|||||
|
|
|
|
¶u |
¶v |
|
|
|||
Так как |
∂z |
= v и |
∂z = u , то dz = udv + vdu . |
|
|
|||||
|
|
|
||||||||
|
¶u |
¶v |
|
|
|
|
|
|||
В силу инвариантности формы первого дифференциала выражение udv + vdu будет дифференциалом функции u × v и в случае, когда u и v являются дифференцируемыми функциями нескольких переменных. Свой- ство (3) доказано.
Пример 2. Найти дифференциал функции |
z = arctg |
y |
. |
|
|||||||||||||||||||||||
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
Решение. Пусть u = |
y |
, тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d |
|
y |
|
|
|
|
|
|||
|
|
|
|
|
y |
|
|
|
|
|
du |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
darctg |
= darctgu = |
|
|
|
= |
|
|
|
x |
= |
|
|
|
|
|||||||||||
|
|
|
|
+ u2 |
|
|
|
|
y 2 |
|
|
|
|
||||||||||||||
|
|
|
|
|
x |
|
1 |
|
|
1 + |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
||||
= |
|
x2 |
× |
xdy - ydx |
= |
xdy - ydx |
= |
|
|
|
x |
|
|
|
|
dy - |
|
ydx |
. |
||||||||
x2 |
+ y2 |
x2 |
x2 + y2 |
|
x |
2 + y |
2 |
|
x2 + y2 |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
Пример |
3. |
|
Найти дифференциал |
|
функции |
|
z = z(u,v) , где |
||||||||||||||||||||
u = x2 + y 2 , v = xy
50
