
14-es / Высшая математика (РТФ) / умк_Цывис_Функции_Интеграл. исчисл
..pdfФункции нескольких переменных, непрерывные на замкнутых огра- ниченных множествах, обладают свойствами, аналогичными свойствам
функции одной переменой, непрерывной на отрезке. |
|
|
|
|||||||||||
Сформулируем некоторые из этих свойств. |
|
|
|
|
||||||||||
1. Если функция |
z = f (M ) |
непрерывна на замкнутом ограниченном |
||||||||||||
множестве |
D, то она ограничена на нем и достигает в некоторых точках |
|||||||||||||
M1 Î D и |
M 2 Î D своих точных верхней и нижней граней. |
|
|
|||||||||||
2. Если функция |
z = f (M ) |
непрерывна на замкнутом связном огра- |
||||||||||||
ниченном множестве D, то она принимает на нем все промежуточные зна- |
||||||||||||||
чения. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3. Если функция |
z = f (M ) |
непрерывна в точке M 0 Î D , то сущест- |
||||||||||||
вует окрестность точки M 0 , в которой данная функция ограничена. |
|
|||||||||||||
4. Если функция непрерывна в точке |
M0 , причем |
f (M0 ) ¹ 0 , то су- |
||||||||||||
ществует окрестность точки M0 , в которой знак |
f (M ) |
совпадает со зна- |
||||||||||||
ком f (M0 ) . |
|
|
|
|
|
|
|
|
|
|
|
|||
5. Если функции |
f (M ) и |
g(M ) определены на множестве D и не- |
||||||||||||
прерывны в точке |
M0 , тогда: |
|
|
|
|
|
|
|
|
|||||
а) f (M ) ± g(M ) непрерывна в точке |
M0 ; |
|
|
|
|
|||||||||
б) |
f (M ) × g(M ) непрерывна в точке |
M0 ; |
|
|
|
|
||||||||
в) |
f (M ) |
непрерывна в точке M0 , при g(M 0 ) ¹ 0 . |
|
|
|
|||||||||
|
|
|
|
|||||||||||
|
g(M ) |
|
|
|
|
|
|
|
|
|
|
|
||
Пусть z = f (x, y) – |
функция |
двух |
|
независимых переменных и |
||||||||||
D( f ) – область |
ее |
определения. |
Выбираем |
произвольную |
точку |
|||||||||
M 0 (x0 , y0 ) Î D( f ) |
и дадим |
x0 приращение |
x , а |
y0 оставим без измене- |
||||||||||
ния. Тогда данная функция f(x,y) |
получит приращение |
|
|
|
||||||||||
|
|
|
|
Dx z = f (x0 + Dx, y0 ) - f (x0 , y0 ) , |
|
|
|
|||||||
которое называется частным приращением функции |
z = f (x, y) |
по пе- |
||||||||||||
ременой x в точке |
M0 (x0 , y0 ) . |
|
|
|
|
|
|
|
|
|||||
Таким же образом, считая |
x0 постоянной и придавая |
y0 прираще- |
||||||||||||
ние y , получим частное приращение функции z = f (x, y) |
по переменой |
|||||||||||||
y в точке |
M0 (x0 , y0 ) |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
Dy z = f (x0 , y0 + Dy) - f (x0 , y0 ) . |
|
|
|
|||||||
31
|
Полным приращением функции |
z = f (x, y) |
в точке |
M0 (x0 , y0 ) на- |
||||||||||||||||
зывается функция |
Dz = Df (x0 , y0 ) = f (x0 + Dx, y0 + Dy) - f (x0 , y0 ) . |
|
||||||||||||||||||
|
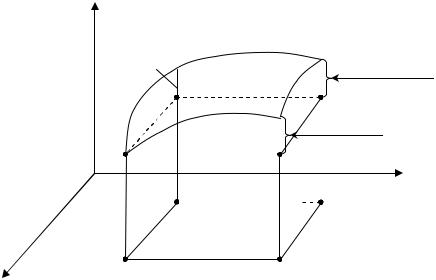
Геометрически |
|
|
частные |
и |
|
полное |
приращение |
|
функции |
||||||||||
Dx z, Dy z, |
Dz – это отрезки (рис. 1). |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x z |
|
|
|
|
B1 |
|
|
|
|
|
|
B3 |
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
A1 |
|
|
|
|
|
|
A3 |
|
|
|
|
|
|
|
|
|
0 |
A0 |
|
|
|
|
|
|
|
|
A2 |
M |
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
x |
|
|
|
M 0 |
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 1 |
|
|
|
|
|
|
|
|
|
|
|
Пример 2. Найти частные и полное приращение функции z = x + y 2 |
|||||||||||||||||||
в точке M 0 (2,1) , если |
|
x = −0,1, |
y = 0,2 . |
|
|
|
|
|
||||||||||||
|
Решение. По определению частных и полного приращения функции |
|||||||||||||||||||
в точке M0 (x0 , y0 ) |
имеем: |
|
|
|
|
|
|
|
|
|
|
|
||||||||
x |
z = f (x + x, y ) − f (x , y ) = (x + |
x) + y2 |
− x |
− y2 = |
x; |
x |
z = −0,1; |
|||||||||||||
|
|
|
0 |
0 |
|
0 |
0 |
0 |
|
|
0 |
0 |
0 |
|
|
|||||
|
D |
y |
z = f (x , y |
0 |
+ Dy) - f (x , y |
0 |
) = x + ( y + Dy)2 - x - y |
2 |
= |
|||||||||||
|
|
0 |
|
|
|
|
0 |
|
|
0 |
0 |
|
0 |
0 |
|
|||||
|
= ( y0 + Dy)2 - y02 = ( y0 + Dy - y0 ) × ( y0 + Dy + y0 ) = Dy × (2 y0 + Dy) |
|||||||||||||||||||
|
Dy z = 0,2 × (2 ×1 + 0,2) = 0, 2 × 2, 2 = 0, 44 |
|
Dy z = 0, 44 |
|||||||||||||||||
z = f (x0 + x, y0 + y) − f (x0 , y0 ) =
=(x0 + Dx + ( y0 + Dy)2 - x0 - y02 = Dx + ( y0 + Dy)2 - y02 =
=Dx + ( y0 + Dy - y0 )( y0 + Dy + y0 ) = Dx + Dy(2 y0 + Dy)
z = −0,1 + 0,44 = 0, 43 .
32
Если w = f (x, y, z) – функция трех независимых переменных, то для
нее вводятся частные и полные приращения |
xw, y w, |
z w и w в |
точке M 0 (x0 , y0 , z0 ) : |
|
|
xw = f (x0 + x, y0 , z0 ) − f (x0 , y0 , z0 ) |
|
|
y w = f (x0 , y0 + y, z0 ) − f (x0 , y0 , z0 ) |
|
|
z w = f (x0 , y0 , z0 + z) − f (x0 , y0 , z0 ) |
|
|
w = f (x0 + x, y0 + y, z0 + z) − f (x0 , y0 , z0 ) . |
|
|
Аналогично определяются частные и полное приращения функции n |
||
независимых переменных. |
|
|
Замечание 1. Определение непрерывности функции нескольких пе- |
||
ременных можно следующим образом: функция |
z = f (x, y) |
непрерывна в |
точке M0 (x0 , y0 ) , если |
lim = f (lim M ) = f (M 0 ) , что равносильно: |
||||||
|
|
M →M 0 |
M →M0 |
||||
"e > 0 |
$dε > 0 |
"M Î D, |
r(M , M0 ) < dε |
|
f (M ) - f (M 0 ) |
|
< e. |
|
|
||||||
Замечание 2. Определение |
непрерывности функции нескольких пере- |
||||||
менных можно дать, используя полное приращение функции z = f (x, y) в точ-
ке М. Функция z = f (x, y) непрерывна в точке M |
|
(x , y ) , если lim z = 0 . |
|||||||
|
|
|
|
|
|
0 |
0 |
0 |
x→0 |
|
|
|
|
|
|
|
|
|
y→0 |
Замечание 3. Функция z = f (x, y) |
называется непрерывной в точке |
||||||||
M 0 (x0 , y0 ) по переменой x, если |
lim |
|
x z = 0 . Аналогично определяется |
||||||
|
|
x→0 |
|
|
|
|
|
||
непрерывность по любой переменой для функции |
n |
независимых пере- |
|||||||
менных. Отметим, что имеет место следующая теорема. |
|||||||||
Теорема 4. Если функция z = f (x1, x2 ,..., xn ) |
определена в точке М |
||||||||
и некоторой ее окрестности и непрерывна в точке |
М, |
то она непрерывна в |
|||||||
этой точке на каждой переменной. |
|
|
|
|
|
|
|
|
|
Заметим, что обратное утверждение неверно. |
|
|
|||||||
Пример 3. Доказать, что функция |
|
|
|
|
|
|
|||
|
xy |
, |
x2 + y2 ¹ 0 |
|
|||||
|
|
|
|
|
|||||
|
+ y2 |
|
|||||||
f (x, y) = x2 |
|
|
|
|
|
|
|||
|
x2 + y2 = 0 |
|
|
|
|
||||
0, |
|
|
|
|
|||||
непрерывна в точке О(0, 0) по каждой переменой x |
и y, но не является |
||||||||
непрерывной как функция двух переменных. |
|
|
|
|
|||||
33
Решение:
1) Найдем частное приращение по x функции f(x,y) в точке О(0, 0)
|
x z = f ( x,0) − f (0,0) = 0 − 0 = 0 . |
|
|
lim |
x z → 0 , а это значит, что f(x,y) непрерывна в точке |
О(0, 0) по |
|
x→0 |
|
|
|
переменой x. |
|
|
|
2) Найдем частное приращение по y функции f(x,y) в точке О(0,0) |
|||
|
y z = f (0, |
y) − f (0,0) = 0 − 0 = 0 . |
|
А lim |
y z = 0 , а это значит, что f(x,y) непрерывна в точке |
О(0,0) по |
|
y →0 |
|
|
|
переменой y. |
|
|
|
3) Докажем, что функция |
z = f (x, y) не является непрерывной в |
||
|
|
|
|
|
|
xy |
|
|
||
точке О(0,0). Для этого найдем lim |
|
|
|
. Если точка M(x, y) стремит- |
||||||
|
|
|
||||||||
|
|
x→0 x |
2 + y 2 |
|
|
|||||
|
|
y→0 |
|
|
|
|
|
|
||
ся к точке О(0, 0) по прямой |
y = kx , тогда получим, что |
|||||||||
|
xy |
|
|
|
|
kx 2 |
k |
|||
lim |
|
= lim |
|
|
|
= |
|
. |
||
|
|
|
|
|
||||||
x→0 x 2 + y 2 |
x→0 x |
2 |
+ k 2 + x 2 |
1 + k 2 |
||||||
y→0 |
|
|
|
|
|
|
|
|
|
|
Следовательно, для различных |
|
k получают разные предельные зна- |
||||||||
чения, а это значит, что предел данной функции в точке О(0,0) не сущест- вует, т.е. функция f(x, y) не является непрерывной в точке О(0,0).
Замечание. При решении данной |
задачи непрерывность функции |
|
f(x,y) по переменным x и y |
можно установить следующим образом: рас- |
|
смотрим функцию f(x,y) при |
y = 0 , т.е. |
f (x,0) , но так как f (x,0) = 0 для |
всех x, то функция f(x, 0) непрерывна на всей числовой оси Ox, в частно- сти и в точке x = 0 . А это означает непрерывность функции f (x, y) в точ-
ке О(0,0) по переменой x.
§7. Дифференцирование функций нескольких переменных
Производная функции y = f (x) одной переменой характеризует ско-
рость изменения функции в точке x. Для случая функции двух или не- скольких переменных можно говорить о скорости изменения функции в точке только в заданном направлении, так как скорость изменения функ- ции двух или нескольких переменных в точке по различным направлениям будет различна.
34
Отношения: |
|
|
|
|
|
|
|
|
|
|
|||
|
z |
= |
f (x + x, y ) − f (x , y ) |
|
y z |
= |
|
f (x , y + y) − f (x , y ) |
|||||
x |
|
0 |
0 |
0 0 |
; |
|
|
|
0 0 |
0 0 |
|
||
|
|
x |
|
y |
|
y |
|||||||
x |
|
|
|
|
|
|
|
||||||
определяют |
среднюю |
скорость изменения |
|
функции |
z = f (x, y) в точке |
||||||||
M0 |
(x0 |
, y0 ) в направлении изменения независимых переменных x и y соответ- |
|
ственно, от точки M0 (x0 , y0 ) до точки M 0 (x0 + x, y0 ) и M 0 (x0 , y0 + |
y) . |
||
|
Частной производной функции z = f (x, y) по переменой x в точке |
||
M0 |
(x0 |
, y0 ) называется предел отношения частного приращения функции |
|
x z к соответствующему отношению приращения аргумента |
x , когда |
||
последнее произвольным образом стремится к нулю:
∂z (M |
0 |
) = lim |
f (x0 + x, y0 ) − f (x0 , y0 ) |
. |
||||
|
||||||||
∂x |
|
x→0 |
|
x |
||||
|
|
|
||||||
Частная производная по переменой |
y определяется аналогично, как |
|||||||
и для переменой x, т.е. |
|
|
|
|
|
|
|
|
∂z (M |
0 ) = lim |
|
f (x0 , y0 + |
y) − f (x0 , y0 ) |
. |
|||
|
|
|
||||||
∂y |
|
|
y →0 |
|
y |
|||
Частные производные для функции n независимых переменных оп- ределяются аналогичным образом.
Следовательно, частная производная функции нескольких независи- мых переменных определяется как производная функции одной из этих переменных при условии, что все остальные переменные остаются посто- янными. Значит, все правила и формулы дифференцирования, справедли- вые для производных функций одной переменой, имеет место и для част- ных производных. Но при этом необходимо помнить, что во всех этих пра-
вилах и формулах при нахождении частной производной по какой-либо переменой все остальные переменные считаются постоянными.
Пример 1. Найти по определению частные производные функции z = x2 + y2 в точке М(1, 2).
Решение. По определению частной производной по переменой x в
точке М(1, 2) имеем |
|
|
|
|
|
|
|
|||
|
∂z |
(M |
0 |
) = lim |
f (x0 + |
x, y0 ) − f (x0 , y0 ) |
= |
|||
|
|
|
|
|
|
|||||
|
∂y |
x →0 |
|
x |
|
|
||||
|
|
|
|
|
||||||
= lim |
(1 + |
|
x)2 + 22 − (12 + 22 ) |
= lim |
x(2 + x) = 2. |
|||||
|
|
|
||||||||
x →0 |
|
x |
|
x →0 |
x |
|||||
35
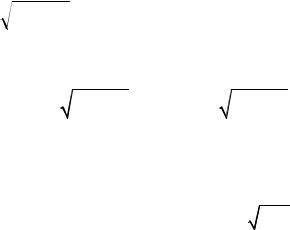
Таким образом |
∂z (M ) = 2 . |
|
|
|
|
||||||
|
|
|
|
¶x |
|
|
|
|
|||
Частная производная по переменой y: |
|
|
|
||||||||
|
¶z |
(M ) = lim |
f (x0 , y0 + |
y) − f (x0 , y0 ) |
= |
|
|||||
|
|
|
|
|
|
|
|||||
|
¶y |
|
y →0 |
Dy |
|
|
|
||||
|
1 + (2 + Dy)2 -1 - 22 |
|
Dy × (4 + Dy) |
|
|||||||
= lim |
|
|
|
= |
lim |
|
|
= 4. |
|||
|
|
|
Dy |
||||||||
y →0 |
|
Dy |
y →0 |
|
|||||||
Таким образом |
∂z |
(M ) = 4 . |
|
|
|
|
|||||
|
|
|
|
|
|||||||
|
|
|
|
¶y |
|
|
|
|
|||
Пример 2. Для функции z = 3x2 y +
ные zx′, zy′ .
Решение. Чтобы найти, например,
x2 - y3 найти частные производ-
частную zx¢ = |
∂z функции двух |
|
¶x |
независимых переменных z = f (x, y) , нужно в выражении f(x,y) второй аргумент y принять за постоянную и дифференцировать f(x,y) как функ-
цию одной переменной x. В нашем случае будем иметь: zx′ = 6xy + 2x .
При дифференцировании по y за постоянную принимаем x, тогда zy′
будет равна zy′ = 3x2 - 3y2 .
Пример 3. Найти все точки, где не существуют частные производ-
ные функции z = 
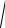 x2 + y2 .
x2 + y2 .
Решение. Находим частные производные функции z:
∂z = |
|
|
x |
|
|
; |
∂z |
= |
|
|
y |
|
. |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
x2 + y2 |
|
|
|
|
|
|||||||||||||||
¶x |
x2 + y2 |
¶y |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Эти формулы теряют смысл в точке |
(0,0). Выясним, имеет ли част- |
||||||||||||||||||||||
ные производные данная функция в точке |
(0, 0). По определению частной |
||||||||||||||||||||||
производной по переменой |
x |
для точки (0, 0) имеем |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
zx¢(0,0) = lim |
f (0 + Dx) - f (0,0) |
= lim |
|
Dx2 |
|
|
= lim |
|
|
Dx |
|
|
. |
||||||||||
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||
|
Dx |
|
|
|
|
|
|
|
|||||||||||||||
x→0 |
|
Dx |
|
|
x→0 |
|
|
x→0 |
|
Dx |
|||||||||||||
Но последний предел не существует, значит, не существует частная производная по x в точке (0, 0).
Поступая таким же образом по y, доказываем, что не существует ча- стная производная по переменой y в точке (0, 0).
36
Физический смысл частной производной:
∂f |
|
∂f |
∂f |
|
|
|
∂x |
(M ), |
∂y (M ), |
∂z (M ) – это скорость изменения функции в точке |
|||
М в направлении оси Ox, Oy и Oz соответственно. |
|
|||||
Геометрический смысл частных производных функции двух неза- |
||||||
висимых переменных. |
|
|
|
|
||
Пусть задана функция |
z = f (x, y) . Выясним геометрический смысл |
|||||
частной |
∂z |
функции |
z = f (x, y) . График функции z = f (x, y) – это не- |
|||
|
∂x |
|
|
|
|
|
которая поверхность Q в |
R3 . Пусть точка P (x , y ) D( f ) , на этой по- |
|||||
|
|
|
|
0 |
0 |
0 |
верхности ей соответствует точка M 0 (x0 , y0 , z0 ) . Пересекаем график дан-
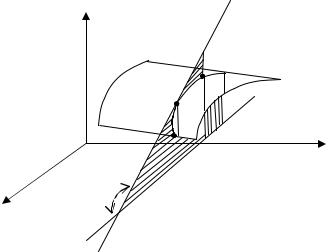
ной функции плоскостью |
y = y0 – получим кривую z = f (x , y0 ) (рис. 1). |
|||||||||||
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B |
|
||
|
M 0 |
|
|
|
А |
|
|
|
y = y0 |
|
||
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
у |
|
|||
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
α |
|
|
P0 |
|
|||||||
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
||
|
Рис. 29 |
|
||||||||||
Это кривая AM 0 B , которая есть график функции одной переменной |
||||||||||||
z = f (x , y0 ) в плоскости |
y = y0 .Тогда по геометрическому смыслу произ- |
|||||||||||
водной функции одной переменой значение частной производной |
∂z |
|||||||||||
∂x |
||||||||||||
функции z = f (x, y) в точке P0 (x0 , y0 ) |
равно численно тангенсу угла α , |
|||||||||||
образованного положительным направлением оси Ox и касательной, про-
веденной в |
точке |
M 0 (x0 , y0 , z0 ) к линии |
пересечения поверхности |
z = f (x, y0 ) |
и плоскости y = y0 . (рис. 1). Аналогичная геометрическая |
||
интерпретация частной производной функции |
z = f (x, y) по y (рис. 2). |
||
37

z
β
P0
x0
y
x |
M 0 |
x = x0
Рис. 2
§ 8. Дифференцируемость функции нескольких переменных
|
Понятие «дифференцируемость функции» |
y = f(x) одной переменой |
||||
было определено следующим образом: функция |
y = f (x) называется диф- |
|||||
ференцируемой в точке x0 , если приращение функции в точке |
x0 |
можно |
||||
представить в виде |
|
|
|
|
||
|
Df (x0 ) = f (x0 + Dx) - f (x0 ) = A(x0 ) × Dx + a(Dx) × Dx , |
|
|
|||
где |
α( x) → 0 |
при x → 0 . |
|
|
|
|
|
Необходимым и достаточным условием дифференцируемости функ- |
|||||
ции |
y = f (x) в точке x0 является существование производной в точке x0 |
|||||
|
|
f ¢(x ) = lim |
f (x0 ) = A(x ) . |
|
|
|
|
|
0 |
Dx |
0 |
|
|
|
|
x→0 |
|
|
|
|
|
Введем понятие дифференцируемости для функции двух перемен- |
|||||
ных z = f (x, y) . |
|
|
|
|
|
|
|
Функция |
z = f (x, y) называется дифференцируемой |
в |
точке |
||
M0 (x0 , y0 ) , если полное приращение функции в этой точке можно пред-
ставить в виде
Dz = f (x0 + Dx, y0 + Dy) - f (x0 , y0 ) = |
|
= A(x0 , y0 )Dx + B(x0 , y0 )Dy + a × Dx + b × Dy , |
(1) |
где α( x, y) → 0 и β( x, y) → 0 при x и y → 0 .
38
Равенство (1) выражает условие дифференцируемости функции z = f (x, y) в точке M0 (x0 , y0 ) .
Функцию z = f (x, y) , дифференцируемую в каждой точке некоторо-
го множества, называют дифференцируемой на этом множестве.
Пример 4. Доказать, что функция z = x2 y дифференцируема на R2 .
Решение. Полное приращение функции в любой точке |
M (x, y) R2 |
||||
имеет вид |
|
|
|
|
|
Dz = f (x + Dx, y + Dy) - f (x, y) = (x + Dx)2 ( y + Dy) - x2 y = |
|
||||
= (x2 + 2xDx + (Dx)2 )( y + Dy) - x2 y = x2 y + 2x × yDx + y(Dx)2 + x2Dy + |
|
||||
|
+2xDx × Dy + Dy × (Dx)2 - x2 y = 2xy × Dx + x2 Dy + |
|
|
||
+( y + Dy) × (Dx) × Dx + 2x × Dx × Dy = A(x, y) × Dx + B(x, y) × Dy + a × Dx + b × Dy, |
|
||||
где A(x, y) = 2xy; |
B = x2; a = ( y + Dy) × Dx; b = 2x × Dx . |
|
|
||
Отметим, что А и |
В в фиксированной точке M0 (x0 , y0 ) – постоян- |
||||
ные числа, а |
α и |
b ® 0 |
при Dx и Dy ® 0 . |
|
|
Это значит, |
что данная функция дифференцируема в любой точке |
||||
M Î R2 . |
|
|
|
|
|
В равенстве |
(1) выражение A × Dx + B × Dy – линейное относительно |
||||
Dx и Dy |
называют главной частью полного приращения функции, |
а |
|||
выражение |
a × Dx + b × Dy |
– является бесконечно малой при |
Dx ® 0 |
и |
|
Dy ® 0 . |
|
|
|
|
|
Следующая теорема устанавливает связь между дифференцируемо- стью и непрерывностью функции двух переменных.
Теорема 5. Если функция z = f (x, y) дифференцируема в точке
M0 (x0 , y0 ) , то она непрерывна в этой точке.
Доказательство. Так как функция |
z = f (x, y) дифференцируема в |
||
точке M0 (x0 , y0 ) , то полное приращение |
z в этой точке имеет вид |
||
|
Dz = A × Dx + B × D + a × Dx + b × Dy, |
(2) |
|
где А и В – |
некоторые числа, не зависящие от Dx и |
Dy ; |
|
α и b |
® 0 при Dx и Dy ® 0 . |
|
|
39
Переходя к пределу в равенстве (2) при x и y → 0 получим
lim Dz = lim ( A × Dx + B × Dy + a × Dx + b × Dy) = 0 |
|
x→0 |
x→0 |
y→0 |
y→0 |
А это значит, что функция z = f (x, y) непрерывна в точке M0 (x0 , y0 ) .
Что и требовалось доказать.
Замечание. Обратная теорема неверна, т.е. непрерывность является только необходимым, но недостаточным условием дифференцируемости функции.
Обратите внимание, что для функции одной переменой y = f (x)
существование производной в точке x0 является необходимым и доста-
точным условием дифференцируемости функции в этой точке.
Для функций нескольких переменных дифференцируемость и суще- ствование частных производных не являются эквивалентными свойствами функции нескольких переменных.
Теорема 6 (необходимое условие дифференцируемости функции).
Если функция z = f (x, y) дифференцируема в точке |
M0 (x0 , y0 ) , то она |
||||
имеет частные производные, причем ∂f (M 0 ) = A, |
∂f |
(M 0 ) = B . |
|
||
|
∂x |
|
∂y |
|
|
Доказательство. Так как функция |
z = f (x, y) |
дифференцируема в |
|||
точке M0 (x0 , y0 ) , то ее полное приращение представимо в виде |
|
||||
Dz = a(x0 , y0 )Dx + B(x0 , y0 )Dy + a × Dx + b× Dy . |
(1) |
||||
Полагая в формуле (1) |
y = 0 , получим Dx z = A × Dx + a × Dx . |
|
|||
Разделим последнее равенство на |
x и, переходя к пределу в полу- |
||||
ченном равенстве при x → 0 , |
получим |
|
|
|
|
lim
x→0
Следовательно, в точке
по переменой y, причем B =
x z = A = |
∂f (x0 , y0 ) . |
x |
∂x |
M0 (x0 , y0 ) существует частная производная
∂f (x0 , y0 ) .
∂y
Теорема доказана.
Теорема обратная для теоремы 6 неверна, т.е. из существования ее частных производных еще не следует дифференцируемость функции (см. пример 3, § 7).
40
