
14-es / Высшая математика (РТФ) / умк_Цывис_Функции_Интеграл. исчисл
..pdf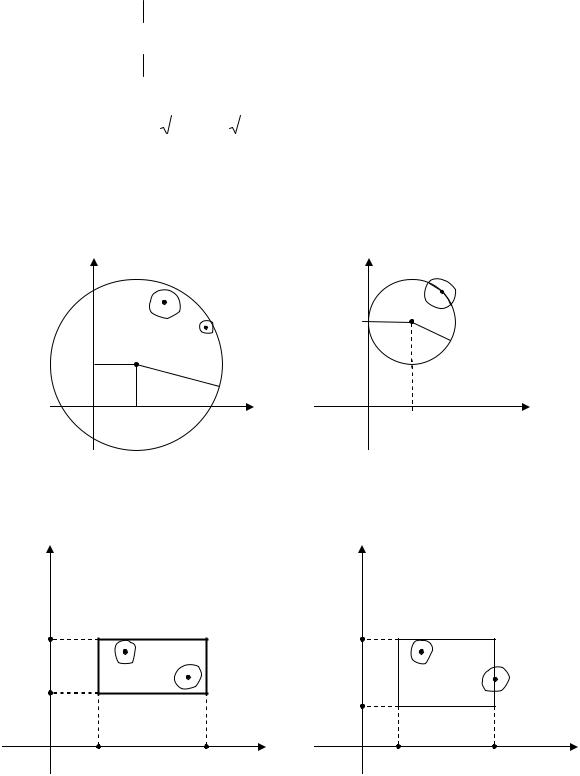
1. E = {(x, y) |
|
(x − 1)2 |
+ ( y − 1)2 |
< 22 } – круг радиуса R = 2 без грани- |
|
||||
1 |
|
|
|
|
цы (рис. 2);
2.E2 = {(x, y) (x − 1) + ( y − 2)2 ≤ 12 } – круг радиуса R = 1 с границей
(рис. 3);
3.E3 = {(x, y)1 < x < 2, 2 y < 3} – прямоугольник без границ (рис.4);
4. |
E4 = {(x, y) |
|
1 ≤ x ≤ 3, 1 ≤ y ≤ 3} – квадрат с границей (рис. 5); |
|||||||||
|
||||||||||||
|
|
= {(x, y) |
|
|
|
− |
|
< x < |
|
|
||
5. |
E |
|
2 |
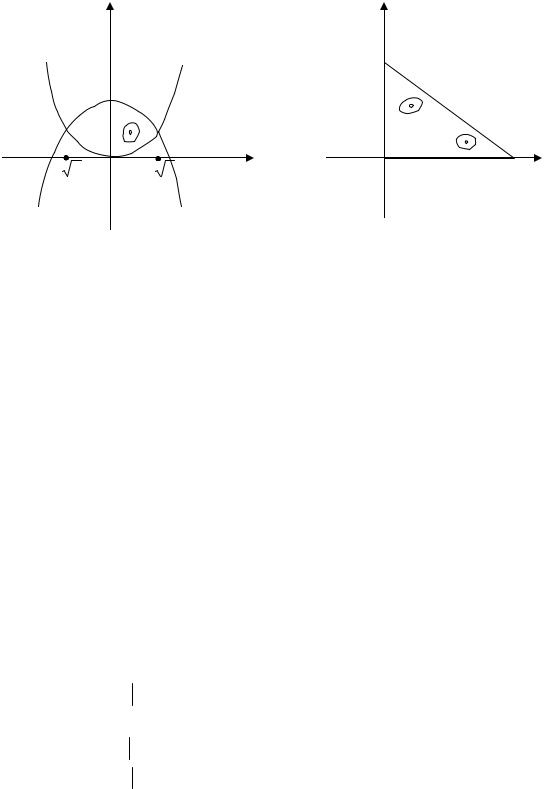
2, x2 < y < 1 − x2 } (рис. 6) |
||||||||
|
5 |
|
|
|
|
|
|
|
|
|
|
|
6. |
E6 |
= {(x, y) |
|
0 < x < 1, 0 < y < 1 − x} – треугольник без границы |
||||||||
|
||||||||||||
(рис. 7).
Множества Е1, |
Е3, Е5, Е6 – открытые. |
|
|
|
|
y |
|
|
y |
|
|
|
|
|
|
|
|
E1 |
|
|
|
|
E2 |
|
|
2 |
|
R = 1 |
|
|
|
|
|
||
1 |
|
R = 2 |
|
|
|
0 |
1 |
x |
0 |
1 |
x |
|
|||||
|
Рис. 2 |
|
|
Рис. 3 |
|
y |
|
|
y |
|
|
|
|
E3 |
|
E4 |
|
|
|
|
|
|
|
3 |
|
|
A |
B |
|
|
|
3 |
|
|
|
2 |
|
|
|
|
|
|
|
|
1 |
|
|
0 |
3 |
x |
0 |
3 |
x |
1 |
1 |
||||
|
Рис. 4 |
|
|
Рис. 5 |
|
11
y |
y |
E5 |
E6 |
y = x2 |
1 |
|
|
1 |
x + y = 1 |
− 2 |
0 |
2 |
x |
0 |
1 x |
Рис. 6 |
Рис. 7 |
Справедливы следующие теоремы:
Теорема 1. Объединение совокупности открытых множеств есть от- крытое множество.
Теорема 2. Пересечение конечного числа открытых множеств есть открытое множество.
Множество Е евклидова пространства R2 замкнуто, если оно со- держит все свои граничные точки (см. например, множество Е2 (рис. 3) или Е4 (рис. 5)). Если из замкнутого множества удалить часть граничных точек (например, из Е4 (рис. 5) удалить сторону АВ), то получим множе- ство, которое не является ни открытым, ни замкнутым.
Множество E Î R 2 замкнуто тогда и только тогда, когда дополнение это- го множества (т.е. множество всех точек R2, которые не входят в Е) открыто.
Множество E Î R 2 называется связным, если любые две точки из Е можно соединить непрерывной кривой, все точки которой принадлежат этому множеству.
Рассмотрим примеры некоторых множеств.
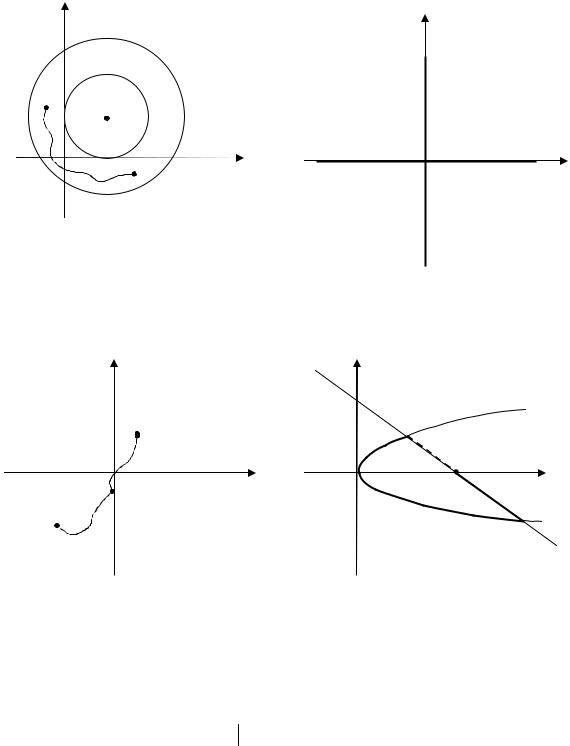
7. E7 = {(x, y) 1 £ (x -1)2 + ( y -1)2 £ 2} (рис. 8), Е7 – связное замк-
нутое множество.
8.E8 = {(x, y) xy < 0} (рис. 9). Е8 – несвязное открытое множество.
9.E9 = {(x, y) xy ³ 0} (рис. 10). Е9 – связное замкнутое множество.
10. E = {(x, y) |
|
x + y < 1, x > y 2 |
} |
(рис. 11). Е10 – связное открытое |
|
||||
10 |
|
|
|
|
множество. |
|
|
||
Множество E Î R 2 называется областью в R2, если данное множе- ство Е связное и открытое.
12
y |
|
y |
|
|
|
|
E7 |
Е8 |
|
|
M1
M2 |
x |
0 |
x |
Рис. 8 |
Рис. 9 |
y |
|
|
y |
|
E9 |
|
x + y = 1 |
1 |
E10 |
|
||||
|
|
|
||
|
M1 |
|
|
|
0 |
|
x |
1 |
x |
|
|
|
x = y2 |
|
M2 |
|
|
|
|
|
|
|
|
|
Рис. 10 Рис. 11
Точка M 0 (x0 , y0 ) называется предельной точкой множества E R 2 ,
если в любой ее окрестности содержаться точки, отличные от M 0 (x0 , y0 ) .
Так, для множества Е точек прямоугольника АВСD (рис. 12)
E = {(x, y) a < x < b, c < y < d}.
Без границы каждая точка (x, y) E является предельной точкой множества. Предельными точками будут и точки границы, например точка (x2 , y2 ) . Точка (x3 , y3 ) предельной точкой множества Е не будет, хотя существует такая окрестность, в которой содержатся точки из Е. (Обрати- те внимание, в определении о предельной точке требуется, чтобы в любой окрестности содержались точки из множества Е).
13
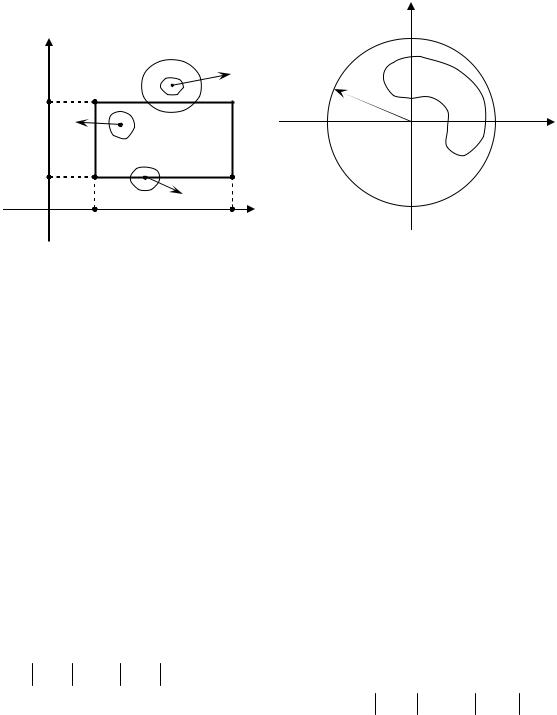
Множество E R 2 ограничено, если оно содержится в некотором круге с центром в начале координат радиусом R, R > 0 (рис. 13).
Замкнутое ограниченное множество Е называется компактным.
y |
|
|
y |
|
|
|
|
|
|
||
|
|
(x3,y3) |
|
|
|
d |
B |
C |
R |
|
|
E |
x |
||||
(x1,y1) |
|
|
|||
|
|
|
|
||
c |
A |
D |
|
|
|
|
|
(x2,y2) |
|
|
|
0 |
a |
b x |
|
|
|
|
Рис. 12 |
|
Рис. 13 |
|
§ 3. Примеры и упражнения
Пример 1. Доказать, что в любой окрестности точки М(a, b), зада-
ваемой неравенством (x − a)2 + ( y − b)2 ≤ R2 , есть окружность, задаваемая
неравенствами |
|
x − a |
|
< δ, |
|
y − b |
|
< δ, |
δ > 0 . |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
Решение. |
|
|
|
Выбирая |
δ > 0 |
такое, |
что |
2δ2 < R2 . Тогда из |
|||||||||||||||
|
x − a |
|
< δ, |
|
y − b |
|
< δ следует, что |
|
|
2 + |
|
|
|
|
2 < 2δ2 < R2 . |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
(x − a)2 + ( y − b)2 = |
|
x − a |
|
|
y − b |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
Пример 2. Пусть множество |
E R 2 |
состоит из точек, обе коорди- |
|||||||||||||||||||||
наты которых |
|
|
|
рациональные числа. Доказать, |
что любая точка |
|||||||||||||||||||||
M (a, b) R 2 (плоскости) является предельной для множества Е.
Решение. Пусть любая окрестность точки М(a, b) задается неравен- ствами x − a < δ, y − b < δ . Тогда существуют рациональные числа r1 и r2, отличные соответственно от а и b, такие, что r1 − a < δ и r2 − b < δ .
Точка B(r1, r2 ) принадлежит множеству Е и находится в выбранной окрестности точки M(a, b) и отлична от М. Таким образом, имеем, что в любой окрестности точки М есть отличные от М точки из множества Е. Значит М(a, b) – предельная точка множества Е.
14
Пример 3. Множество Е состоит из точек плоскости, для которых x2 + y2 <100 . Доказать, что точка M(6, 8) является предельной для множе-
ства Е.
Решение. Выбираем любую окрестность точки М(6, 8), задаваемую
неравенствами |
|
x - 6 |
|
< d, |
|
y - 8 |
|
< d, где 0 < δ < 1. Тогда |
|
6 |
- |
d |
- |
d |
|
|
|
|
|||||||||||
|
|
|
|
B |
, 8 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
принадлежит этой окрестности, причем
|
6 |
- |
d 2 |
|
8 |
- |
d 2 |
< 6 |
2 |
+ 8 |
2 |
=100 |
|
|
+ |
|
|
|
|||||||
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
Значит, точка В принадлежит множеству Е, откуда имеем, что М – предельная точка для множества Е.
Пример 4. Доказать, что множество Е точек плоскости, удовлетво-
ряющих неравенству y ³ x2 , замкнуто.
Решение. По определению замкнутое множество – это множество, которое содержит все свои предельные точки. Значит, чтобы доказать
замкнутость множества |
Е достаточно показать, что любая |
М(a, b), не |
||||||||||||||||||||||||||||||||||
принадлежащая |
Е не может быть предельной |
для |
Е. Пусть точка M(a, b) |
|||||||||||||||||||||||||||||||||
не принадлежит |
Е. Тогда имеем неравенство |
b < a2 . Пусть e = a2 - b > 0 , |
||||||||||||||||||||||||||||||||||
тогда найдется |
такое |
δ < |
ε |
, что |
|
|
|
из неравенства |
|
|
|
x − a |
|
< δ |
вытекает |
|||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||
|
|
x2 - a2 |
|
|
ε |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
< |
|
|
|
|
|
|
|
x - a |
|
< d , |
|
y - b |
|
< d следует, что |
|||||||||||||||||||
|
|
|
. Тогда из неравенства |
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
x2 - y = (a2 - b) + (b - y) + (x2 - a2 ) ³ |
|
||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
³ (a2 - b) - |
|
b - y |
|
- |
|
x2 - a2 |
|
> e - |
e |
- |
e |
= 0. |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Значит, все точки δ – окрестности точки М не принадлежат множе- ству Е. Значит, множество Е замкнуто.
Пример 5. Найти граничные точки множества Е, заданного неравен-
ством x 2 + y 2 < 25 .
Решение. Граничными точками множества E Î R 2 называются точ- ки, в любой окрестности которых есть как точки из множества Е, так и точки, не принадлежащие этому множеству. Данное множество состоит из точек, лежащих внутри окружности радиуса 5 с центром в начале коорди- нат (точки самой окружности не принадлежат множеству). С геометриче-
15

ской точки зрения границей множества Е – окружность x 2 + y 2 = 25 . До-
кажем это аналитически. Неравенства x 2 + y 2 < 25 и x 2 + y 2 > 25 задают открытые множества, следовательно, ни точки множества x 2 + y 2 < 25 , ни точки множества x 2 + y 2 > 25 не являются граничными для множества Е.
Рассмотрим теперь точки окружности |
x 2 + y 2 = 25 . Пусть |
|
А(a, b) |
||||||
лежит на этой окружности. Выберем любую окрестность точки |
А. В эту |
||||||||
окрестность точки А попадают как точки |
B(x, y), для которых |
|
x |
|
< |
|
a |
|
, |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
y < b так и точки, для которых x > a , y > b . Для первых точек имеем
x 2 + y 2 < a 2 + b2 = 25 , а для вторых – x 2 + y 2 >100 . Значит, A(a, b) – гра-
ничная точка для Е.
Задачи для самостоятельной работы
1.Множество Е состоит из всех точек плоскости, обе координаты которых иррациональные числа. Доказать, что любая точка плоскости яв- ляется предельной точкой для множества Е.
2.Множество Е состоит из всех точек плоскости, абсцисса которых рациональна, а ордината иррациональна. Доказать, что любая точка плос- кости является предельной для множества Е.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
1 |
||
|
3. Множество Е состоит из всех точек плоскости вида |
|
A |
|
|
, |
|
, |
||||||||||||
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
n |
||||
где m и n – |
натуральные числа. Найдите предельные точки множества Е. |
|||||||||||||||||||
|
Ответ: |
предельными точками для множества |
Е являются все точки |
|||||||||||||||||
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
||
вида |
|
|
; 0 |
, |
0; |
|
и (0, 0). |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
m |
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|||||
|
4. Построить хотя бы одно множество, для которого предельными |
|||||||||||||||||||
были бы точки А(3, 4) и В(–1, 2), и только эти точки. |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
Ответ: |
|
например, |
множество |
точек |
A 3 + |
|
, 4 |
|
|
и |
|||||||||
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
n |
|
|
|
|||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B |
−1 + |
|
, 2 |
, n N . |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||
n |
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
5. Построить множество, предельными точками для которого явля- ются все точки вида А(0, n), n – целое число, и только такие точки.
1
Ответ: например, множество точек
m
,n , m R.
16
6. Доказать, что множество точек плоскости, координаты которых удовлетворяют системе неравенств
x + y > 5
2 + 2 <
x y 100
открыто.
7. Доказать, что множество точек плоскости, координаты которых удовлетворяют неравенствам
x + y ³ 5 |
|
|
+ y2 £100 |
x2 |
|
замкнуто. |
|
8. Доказать, что множество |
E = ( A Ç B) È (C Ç D) замкнуто. Если А |
задается неравенством y ³ x2 , В – неравенством x2 + y2 £ 49 , С – нера-
венством x + y ³ 3 и D – неравенством (x - 4)2 + ( y -1)2 £ 81. 9. Какие из данных множеств являются областями:
1)множество точек, удовлетворяющих неравенству
1< x2 + y2 < 16 ;
2)множество точек, удовлетворяющих системе неравенств
4 < x2 + y2 <10
-1 < y <1;
3)множество, состоящее из двух открытых кругов радиуса 6 с цен- тром в точках О(0, 0) и А(12, 0) соответственно;
4)множество, состоящее из тех же кругов (пункт 3) и точки С(6, 0) Отметим, что множество Е называется областью, если оно открыто
илюбые две его точки можно соединить линией, полностью лежащей в множестве Е.
Ответ: 1) область; 2) не область; 3) не область; 4) не область.
|
|
§4. Функции двух переменных. |
|
|
Понятие функции n переменных |
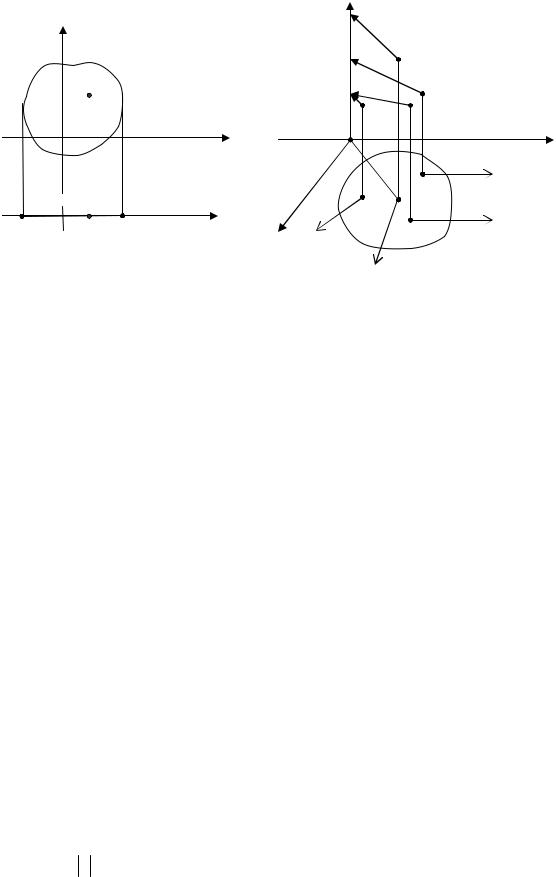
Функцией двух независимых переменных (x, y), определенной на |
||
множестве |
D Î R2 |
, называется соответствие f, которое каждому элементу |
(x, y) Î D |
ставит |
в соответствие единственный элемент F R , обозна- |
чаемый f(x, y) (рис. 1, 2).
17
z z1
y |
|
R 2 |
|
z2 |
|
|
|
|
|
|
D |
|
|
z3 = z4 |
|
(x,y) |
|
|
|
|
|
|
|
|
0 |
|
|
x |
y |
|
|
|
|
|
|
|
|
|
(x2 , y2 ) |
|
f(x,y) |
R |
|
D |
|
|
(x4 , y4 ) |
||
0 |
F |
|
|
|
|
|
x (x3 , y3 ) |
||
|
|
|
|
|
|
|
|
|
(x1 , y1 ) |
Рис. 1 |
|
|
Рис. 2 |
|
Множество D называют областью определения (множество заданий) функции f, а совокупность (множество) всех элементов f(x, y), (x, y) D –
множеством значений |
E(f) функции f. Тот факт, что f – функция, задан- |
ная (область определения) на D R2 , со значениями в E R , обозначают |
|
следующим образом |
f : D → E . |
Соответственно |
f, устанавливаемое между точками из D R2 и |
E R , геометрически можно изобразить в пространстве R3 (рис. 2). Функцию Z = f (x, y) – двух переменных можно задать:
–аналитическим способом (используя формулы);
–табличным (используя таблицы);
–графическим (построить график);
–программным (построить алгоритм вычисления z по x и y).
Графиком Г f функции f называется множество точек пространст-
ва R3 с координатами (x, y, f(x, y)), (x, y) D , т.е.
Г f = {(x, y, z) /(x, y) D, z = f (x, y)}.
Для построения графика функции Г f – функции двух переменных из точки (x, y) D( f ) перпендикулярно к плоскости Oxy отложим отре-
зок длиной z в положительном направлении оси Oz, если z > 0, и в отри-
18

цательном направлении, если z < 0. Точка пространства R3 с координата- ми (x, y, z) будет точкой графика Г f .
График функции Г f , вообще говоря, есть некоторая поверхность в
R3 . Проекцией этой поверхности на плоскость Oxy является область D(f).
Соответствие, устанавливаемое между элементами (x, y, z) D R3
и элементами множества E R , при котором каждому элементу из D ставится в соответствие один элемент из Е, называется функцией трех пе- ременных. Область определения D данной функции есть множество точек пространства R3 . Поскольку каждая точка (x, y, z) определяет в про-
странстве R3 радиус-вектор, то функцию f трех переменных можно рас- сматривать как соответствие, устанавливаемое между множеством векто- ров и множеством действительных чисел. Значит, функцию трех перемен- ных можно рассматривать как скалярную функцию векторного аргумента. График функции трех переменных определяется аналогично, но изобра- зить графически функцию трех и более переменных невозможно.
Рассмотрим примеры функций двух переменных и их графики:
1) |
f = x2 + y 2 . Область определения функции |
D( f ) = R2 , множество |
||
значений |
E( f ) = [0; + ∞), график функции в R3 – |
круговой параболоид |
||
(рис. 3); |
|
|
|
|
|
f = |
|
. Область определения |
D( f ) = R2 , множество |
2) |
4 − x2 − 4 y 2 |
|||
значений |
E( f ) = [0; 2], график функции изображен на рис. 4; |
|||
z
z
2
y |
2 |
y |
1
x
x
Рис. 3 |
Рис. 4 |
19
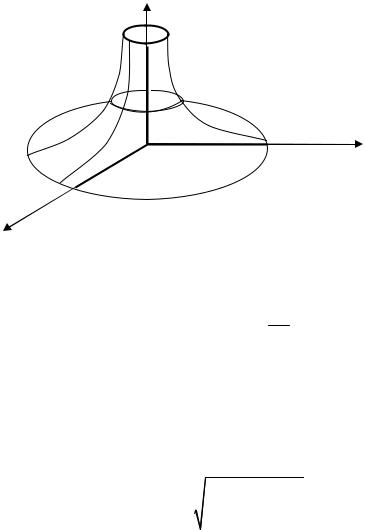
3) |
f = |
|
|
1 |
. Область определения D( f ) = R |
2 |
\ (0, 0) . Множество |
x |
2 |
+ y 2 |
|
||||
|
|
|
|
|
|||
значений |
E( f ) (0; + ∞), график функции изображен на рис. 5. |
||||||
z
0 |
y |
x
Рис. 5
Понятие функций n переменных. Множество всех упорядоченных совокупностей (x1, x2 ,...xn ) , где xn R, k = 1, n называется n-мерным ко-
ординатным пространством Rn , а каждая упорядоченная совокупность
(x1, x2 ,...xn ) = M – |
точкой этого пространства. Координатное пространство |
||||||
Rn |
называется |
декартовым, если |
|
расстояние между |
точками |
||
M (x1, x2 ,...xn ) и |
N ( y1, y2 ...yn ) определяется по формуле |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
n |
|
− x )2 . |
|
|
|
|
ρ(M , N ) = ∑ ( y |
k |
|
|||
|
|
|
k =1 |
k |
|
||
|
|
|
|
|
|
|
|
|
Евклидово n-мерное пространство является обобщением понятий |
||||||
евклидовой прямой R1 , евклидовой плоскости R2 , евклидова пространст- |
|||||||
ва |
R3 . |
|
|
|
|
|
|
|
Если каждой точке M D Rn евклидова пространства |
Rn по не- |
|||||
которому закону (правилу) f ставится в соответствие одно из чисел мно-
жества |
E Ì R , то говорят, что на D |
задана функция f. Множество |
D – |
область определения функции f; Е – |
множество значений функции f. Ана- |
||
логично, |
как для R1, R2 , R3 , так и для Rn вводится понятие графика |
||
функции, но для n ³ 3 построить (изобразить) поверхность для n ³ 3 |
не- |
||
возможно (можно только представить!). |
|
||
20
