- •3 Семестр (часть 1). Дифференциальные уравнения
- •1. Общие понятия
- •3. Дифференциальные уравнения с разделяющимися переменными. Однородные уравнения
- •1. Линейные дифференциальные уравнения. Метод вариации произвольной постоянной
- •2. Задача Коши. Теорема существования и единственности решения задачи Коши. Общее решение и общий интеграл
- •3. Уравнения, допускающие понижение порядка
- •1. Свойства дифференциального оператора. Теорема Коши
- •2. Линейная зависимость и линейная независимость системы функций. Вронскиан. Исследование линейной независимости с помощью вронскиана
- •3. Структура общего решения однородного дифференциального уравнения
- •Лекция 4. Общее решение неоднородного уравнения. Метод вариации произвольных постоянных Лагранжа. Комплексные решения дифференциальных уравнений. Построение фундаментальной системы решений
- •1. Структура общего решения неоднородного уравнения. Метод вариации произвольных постоянных Лагранжа
- •2.Метод вариации произвольных постоянных Лагранжа
- •3. Комплексные решения дифференциальных уравнений. Линейная независимость комплексных решений
- •Лекция 5. Линейные дифференциальные уравнения с постоянными коэффициентами. Метод Эйлера и метод подбора вычисления частных решений неоднородных уравнений
- •1. Метод Эйлера построения общего решения однородного дифференциального уравнения с постоянными коэффициентами в случае простых корней характеристического уравнения
- •2. Построение общего решения однородного дифференциального уравнения в случае кратных корней характеристического уравнения
- •3. Построение общего решения неоднородного уравнения с постоянными коэффициентами. Метод подбора частного решения неоднородного уравнения
- •Лекция 6. Комплексные числа и действия над ними. Функции комплексного переменного. Предел и непрерывность. Элементарные функции комплексного переменного и действия над ними
- •1. Извлечение корня й степени из комплексного числа. Множества в комплексной плоскости
- •2. Предел и непрерывность функции комплексной переменной
- •Лекция 7. Производная функции комплексного переменного. Аналитичность функции в точке и в области. Условия Коши-Римана. Элементарные аналитические функции
- •2. Геометрический смысл модуля и аргумента производной
- •Лекция 8 . Интеграл от функции комплексного переменного. Теорема Коши и для односвязной и многосвязной областей. Интегральная формула Коши. Существование всех производных для аналитической функции
- •2.2. Теорема Коши для односвязной области и многосвязной области. Интегральная формула Коши
- •3. Первообразная функции комплексных переменных
- •Лекция 9. Ряды в комплексной области. Степенные ряды. Теорема Абеля. Ряды Тейлора и Лорана
- •1. Степенные ряды. Ряды Тейлора и Лорана
- •Лекция 10. Изолированные особые точки. Ряды Лорана для функций, аналитических в кольце
- •1. Разложение функции в ряд Лорана
- •2. Нули аналитической функции и их связь с полюсами
- •3. Вычеты. Теорема Коши о вычетах
- •Лекция 11. Вычисление вычетов и применение теории вычетов для вычисления контурных и несобственных интегралов
- •1. Вычисление вычетов
- •2. Вычисление интегралов
- •Лекция 12. Преобразование Лапласа и его свойства. Применение к дифференциальным уравнениям
- •Лекция 13. Системы дифференциальных уравнений. Общие понятия
- •1. Понятия общего и частного решений. Задача Коши и ее разрешимость
- •2. Методы интегрирования систем дифференциальных уравнений
- •Лекция 14. Системы линейных дифференциальных уравнений
- •1. Глобальная теорема разрешимости начальной задачи для линейной системы дифференциальных уравнений
- •2. Линейная зависимость и линейная независимость системы произвольных вектор-функций и решений однородной системы уравнений
- •3. Фундаментальная матрица решений и структура общего решения однородной системы
- •4. Структура общего решения неоднородной системы дифференциальных уравнений
- •Лекция 15. Построение фундаментальной матрицы решений дифференциальной системы с постоянной матрицей. Метод Эйлера.
2. Построение общего решения однородного дифференциального уравнения в случае кратных корней характеристического уравнения
Напомним сначала,
что корень
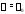 характеристического многочлена
характеристического многочлена называется
корнем кратности
называется
корнем кратности
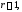 если
если
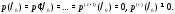
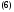
Полезно заметить,
что если полином
 имеет
имеет различных корней
различных корней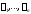 (
( – степень многочлена
– степень многочлена ),
то все они имеют кратность
),
то все они имеют кратность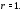 Однократные корни называют еще
простыми корнями
Однократные корни называют еще
простыми корнями
 .
.
Записав для
многочлена
 формулу Тейлора
формулу Тейлора

(остаточный член
его равен тождественно нулю), получим
с учетом равенств (6), что если
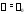 – корень кратности
– корень кратности ,
то
,
то представляется в виде
представляется в виде
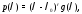

где
 – многочлен степени
– многочлен степени такой, что
такой, что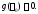 Очевидно, верно и обратное: если
Очевидно, верно и обратное: если представляется в виде (7)
, где
представляется в виде (7)
, где
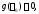 то
то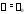 –- корень кратности
–- корень кратности многочлена
многочлена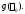
Построению
фундаментальной системы решений в
случае кратных корней характеристического
уравнения
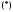 предпошлем несколько вспомогательных
утверждений.
предпошлем несколько вспомогательных
утверждений.
 Если
Если
 – дифференциальный оператор с постоянными
коэффициентами
– дифференциальный оператор с постоянными
коэффициентами то имеет место формула
то имеет место формула

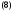
Действительно, по (2) имеем
 Дифференцируя это тождество по
Дифференцируя это тождество по и учитывая, что операторы
и учитывая, что операторы и
и перестановочны при применении их к
бесконечно дифференцируемой по
перестановочны при применении их к
бесконечно дифференцируемой по и
и функции
функции ,
будем иметь
,
будем иметь
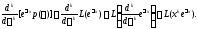
Таким образом, справедливо тождество (8).
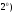 Пусть
Пусть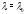 – корень кратности
– корень кратности характеристического многочлена
характеристического многочлена уравнения (21.26) с постоянными коэффициентами
уравнения (21.26) с постоянными коэффициентами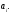 Тогда
Тогда функций
функций
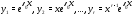
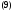
линейно независимы на любом отрезке
 и являются решениями уравнения (1).
и являются решениями уравнения (1).
Доказательство.Пусть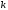 –- любое натуральное число, удовлетворяющее
неравенству
–- любое натуральное число, удовлетворяющее
неравенству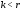 .
Согласно
.
Согласно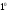 имеет место тождество
имеет место тождество

где
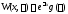 (см.
(см.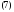 ).
Имеем
).
Имеем


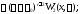

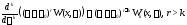
Полагая в последнем тождестве
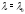 ,
будем иметь
,
будем иметь
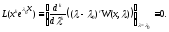
Это означает, что функции (9) являются
решениями уравнения (1). Эти функции
линейно независимы на любом отрезке
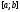 (см. утверждение
(см. утверждение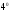 предыдущей лекции). Свойство
предыдущей лекции). Свойство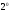 доказано.
доказано.
Если
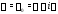 – комплексный корень кратности
– комплексный корень кратности уравнения
уравнения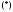 с постоянными и действительными
коэффициентами
с постоянными и действительными
коэффициентами ,
то отделяя в (9) действительные и мнимые
части, получаем
,
то отделяя в (9) действительные и мнимые
части, получаем линейно независимых действительных
решений
линейно независимых действительных
решений
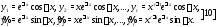
Из этого факта и предыдущих утверждений
вытекает следующий алгоритм построения
фундаментальной системы решений
однородного уравнения (1) с постоянными
и действительными коэффициентами
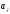 .
.
Алгоритм 1.
1) По уравнению (1) составляем
характеристическое уравнение
 ,
заменив в (1) производные
,
заменив в (1) производные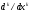 на степени
на степени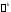 (
(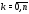 ).
).
2) Найдем корни
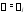 характеристического уравнения
характеристического уравнения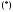 и установим их кратности.
и установим их кратности.
3) Каждому действительному корню
 кратности
кратности поставим в соответствие
поставим в соответствие линейно независимых решений
линейно независимых решений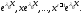
4) Каждой паре комплексно-сопряженных
корней
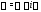 кратности
кратности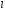 сопоставим
сопоставим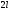 линейно независимых решений
линейно независимых решений
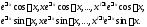
5) Объединим все полученные линейно
независимые решения. Получим фундаментальную
систему решений уравнения (1), состоящую
из
 функций (
функций ( –
порядок уравнения (1)).
–
порядок уравнения (1)).
Общее решение уравнения (1) имеет вид
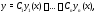
где
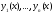 – построенная в алгоритме 1 фундаментальная
система решений, а
– построенная в алгоритме 1 фундаментальная
система решений, а –- произвольные постоянные.
–- произвольные постоянные.
Пример 2.Найти общее решение
уравнения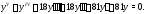
Решение. Составляем характеристическое
уравнение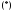 ,
находим его корни и устанавливаем их
кратности:
,
находим его корни и устанавливаем их
кратности:

Согласно алгоритму 1 выписываем линейно независимые решения, отвечающие каждому корню:
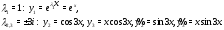
Следовательно, общее решение исходного уравнения имеет вид