
- •3 Семестр (часть 1). Дифференциальные уравнения
- •1. Общие понятия
- •3. Дифференциальные уравнения с разделяющимися переменными. Однородные уравнения
- •1. Линейные дифференциальные уравнения. Метод вариации произвольной постоянной
- •2. Задача Коши. Теорема существования и единственности решения задачи Коши. Общее решение и общий интеграл
- •3. Уравнения, допускающие понижение порядка
- •1. Свойства дифференциального оператора. Теорема Коши
- •2. Линейная зависимость и линейная независимость системы функций. Вронскиан. Исследование линейной независимости с помощью вронскиана
- •3. Структура общего решения однородного дифференциального уравнения
- •Лекция 4. Общее решение неоднородного уравнения. Метод вариации произвольных постоянных Лагранжа. Комплексные решения дифференциальных уравнений. Построение фундаментальной системы решений
- •1. Структура общего решения неоднородного уравнения. Метод вариации произвольных постоянных Лагранжа
- •2.Метод вариации произвольных постоянных Лагранжа
- •3. Комплексные решения дифференциальных уравнений. Линейная независимость комплексных решений
- •Лекция 5. Линейные дифференциальные уравнения с постоянными коэффициентами. Метод Эйлера и метод подбора вычисления частных решений неоднородных уравнений
- •1. Метод Эйлера построения общего решения однородного дифференциального уравнения с постоянными коэффициентами в случае простых корней характеристического уравнения
- •2. Построение общего решения однородного дифференциального уравнения в случае кратных корней характеристического уравнения
- •3. Построение общего решения неоднородного уравнения с постоянными коэффициентами. Метод подбора частного решения неоднородного уравнения
- •Лекция 6. Комплексные числа и действия над ними. Функции комплексного переменного. Предел и непрерывность. Элементарные функции комплексного переменного и действия над ними
- •1. Извлечение корня й степени из комплексного числа. Множества в комплексной плоскости
- •2. Предел и непрерывность функции комплексной переменной
- •Лекция 7. Производная функции комплексного переменного. Аналитичность функции в точке и в области. Условия Коши-Римана. Элементарные аналитические функции
- •2. Геометрический смысл модуля и аргумента производной
- •Лекция 8 . Интеграл от функции комплексного переменного. Теорема Коши и для односвязной и многосвязной областей. Интегральная формула Коши. Существование всех производных для аналитической функции
- •2.2. Теорема Коши для односвязной области и многосвязной области. Интегральная формула Коши
- •3. Первообразная функции комплексных переменных
- •Лекция 9. Ряды в комплексной области. Степенные ряды. Теорема Абеля. Ряды Тейлора и Лорана
- •1. Степенные ряды. Ряды Тейлора и Лорана
- •Лекция 10. Изолированные особые точки. Ряды Лорана для функций, аналитических в кольце
- •1. Разложение функции в ряд Лорана
- •2. Нули аналитической функции и их связь с полюсами
- •3. Вычеты. Теорема Коши о вычетах
- •Лекция 11. Вычисление вычетов и применение теории вычетов для вычисления контурных и несобственных интегралов
- •1. Вычисление вычетов
- •2. Вычисление интегралов
- •Лекция 12. Преобразование Лапласа и его свойства. Применение к дифференциальным уравнениям
- •Лекция 13. Системы дифференциальных уравнений. Общие понятия
- •1. Понятия общего и частного решений. Задача Коши и ее разрешимость
- •2. Методы интегрирования систем дифференциальных уравнений
- •Лекция 14. Системы линейных дифференциальных уравнений
- •1. Глобальная теорема разрешимости начальной задачи для линейной системы дифференциальных уравнений
- •2. Линейная зависимость и линейная независимость системы произвольных вектор-функций и решений однородной системы уравнений
- •3. Фундаментальная матрица решений и структура общего решения однородной системы
- •4. Структура общего решения неоднородной системы дифференциальных уравнений
- •Лекция 15. Построение фундаментальной матрицы решений дифференциальной системы с постоянной матрицей. Метод Эйлера.
Лекция 6. Комплексные числа и действия над ними. Функции комплексного переменного. Предел и непрерывность. Элементарные функции комплексного переменного и действия над ними
Комплексные числа и действия над ними
были определены ранее (см. лекцию 4).
Напомним их. Комплексными числаминазывают числа вида где
где и
и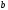 – действительные числа,
– действительные числа, мнимая единица (
мнимая единица (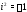 ).
При этом число
).
При этом число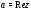 называется действительной частью,
а число
называется действительной частью,
а число – мнимой частьюкомплексного числа
– мнимой частьюкомплексного числа .
Число
.
Число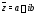 называется сопряженнымк числу
называется сопряженнымк числу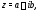 а неотрицательное число
а неотрицательное число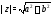 называется модулемчисла
называется модулемчисла .
Множество всех комплексных чисел
обозначают буквой
.
Множество всех комплексных чисел
обозначают буквой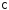 .
P1.eps Каждому комплексному числу
.
P1.eps Каждому комплексному числу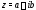 соответствует единственная точка
соответствует единственная точка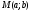 на плоскости
на плоскости или радиус-вектор
или радиус-вектор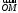 этой точки. При этом ось
этой точки. При этом ось называется действительной осью, с
ось
называется действительной осью, с
ось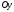 – мнимой осью. Сама плоскость
– мнимой осью. Сама плоскость называется комплексной плоскостью;
ее тоже обозначают буквой
называется комплексной плоскостью;
ее тоже обозначают буквой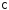 .
Угол
.
Угол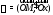 называется аргументомкомплексного
числа
называется аргументомкомплексного
числа .
Ясно, что аргумент определяется
неоднозначно. Главным значениемаргумента называется угол
.
Ясно, что аргумент определяется
неоднозначно. Главным значениемаргумента называется угол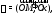 лежащий в пределах
лежащий в пределах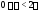 (или в пределах
(или в пределах ).
Главное значение аргумента обозначается
так:
).
Главное значение аргумента обозначается
так: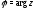 .
Из рис. 1 видно, что
.
Из рис. 1 видно, что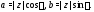 Значит, комплексное число можно записать
еще в виде
Значит, комплексное число можно записать
еще в виде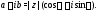 Эта форма называется тригонометрической
формойчисла
Эта форма называется тригонометрической
формойчисла ,
а его первоначальная форма
,
а его первоначальная форма –алгебраической формой комплексного
числа
–алгебраической формой комплексного
числа .
Если воспользоваться формулой Эйлера
.
Если воспользоваться формулой Эйлера то
можно получить еще одну форму комплексного
числа
то
можно получить еще одну форму комплексного
числа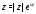 называемую показательной формойчисла3
называемую показательной формойчисла3 Два
комплексных числа называются равными,
если равны одновременно порознь
действительные и мнимые части этих
чисел, т.е.
Два
комплексных числа называются равными,
если равны одновременно порознь
действительные и мнимые части этих
чисел, т.е.

Действия над комплексными числами определяются равенствами:
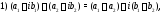

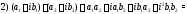
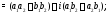
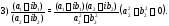
Умножение комплексных чисел (и их деление) лучше производить в тригонометрической форме:
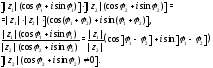
(эти формулы легко получить, используя равенства 1–2). Отсюда вытекает следующее равенство

Действительно, применяя первую из
предыдущих формул
 раз, будем иметь
раз, будем иметь
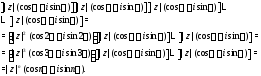
1. Извлечение корня й степени из комплексного числа. Множества в комплексной плоскости
Равенство (1) называется формулой
Муавра. Используя его, можно вывести
формулу извлечения корня й
степени из комплексного числа. Однако
для этого надо ввести сначала понятие
корня.
й
степени из комплексного числа. Однако
для этого надо ввести сначала понятие
корня.
Определение 1. Корнем й
степени из комплексного числа
й
степени из комплексного числа называется такое комплексное число
называется такое комплексное число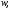
 я
степень которого равна
я
степень которого равна Обозначение:
Обозначение: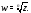
Таким образом,
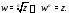 Пусть
Пусть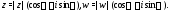 Имеем
(при
Имеем
(при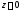 )
)
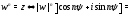

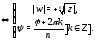
Значит,
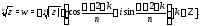 Изменяя
здесь
Изменяя
здесь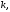 видим, что различные значения корня
видим, что различные значения корня й
степени получаются при
й
степени получаются при Дальнейшее изменение
Дальнейшее изменение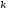 привело бы к уже полученным значениям
привело бы к уже полученным значениям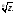 Если же
Если же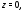 то,
очевидно,
то,
очевидно,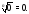 Мы доказали следующий результат.
Мы доказали следующий результат.
Теорема 1.Если
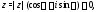 то
корень
то
корень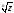 имеет ровно
имеет ровно различных значений:
различных значений: Если
Если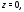 то
то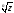 имеет
только одно значение, равное нулю.
имеет
только одно значение, равное нулю.
Например,
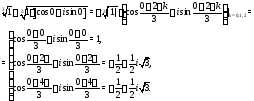
Приведем примеры простейших множеств точек на комплексной плоскости:
а)
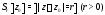 –
окружность с центром в точке
–
окружность с центром в точке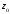 радиусом
радиусом ;
;
б)
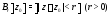 –
открытый круг с центром в точке
–
открытый круг с центром в точке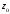 радиусом
радиусом ;
;
в)
 –
внешность открытого круга с центром в
точке
–
внешность открытого круга с центром в
точке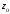 радиусом
радиусом ;
;
г)
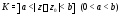 – открытое кольцо с центром в точке
– открытое кольцо с центром в точке ;
;
д)
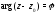 – луч с началом в точке
– луч с началом в точке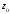 ,
идущий под углом
,
идущий под углом к положительному направлению действительной
оси;
к положительному направлению действительной
оси;
е)
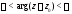 – внутренность неограниченного открытого
сектора с вершиной в точке
– внутренность неограниченного открытого
сектора с вершиной в точке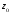 и углом
и углом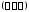 ;
;
ж)
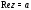 – прямая, параллельная мнимой оси,
проходящая через точку
– прямая, параллельная мнимой оси,
проходящая через точку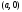 ;
;
з)
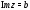 – прямая, параллельная действительной
оси, проходящая через точку
– прямая, параллельная действительной
оси, проходящая через точку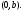
и)
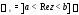 вертикальная
полоса между прямыми
вертикальная
полоса между прямыми и
и
к)
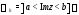 горизонтальная полоса между прямыми
горизонтальная полоса между прямыми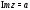 и
и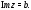
Рекомендуем сделать рисунки всех перечисленных множеств. В качестве упражнения попробуйте записать аналитичеcки (в виде уравнений или неравенств) приводимые ниже множества на комплексной плоскости.
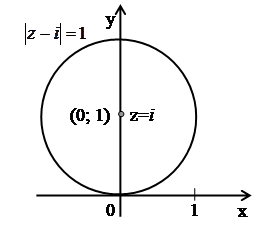
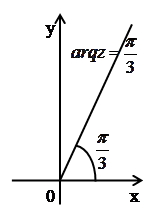
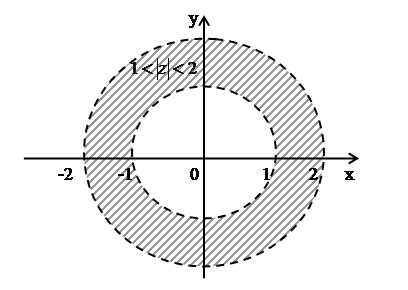
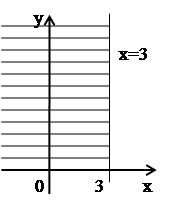
Рис. 2
Понятие окрестности точки вводится также, как и в действительном анализе.
Определение 2.
 окрестностью точки
окрестностью точки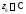 называется открытый круг
называется открытый круг

с центром в точке
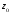 радиуса
радиуса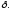 Проколотой
Проколотой
 окрестностью точки
окрестностью точки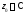 называется множество
называется множество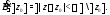
Определение 3. Точка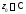 называетсявнутренней точкой множества
называетсявнутренней точкой множества
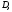 если она входит в
если она входит в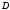 вместе с некоторой своей окрестностью.
Если все точки множества
вместе с некоторой своей окрестностью.
Если все точки множества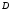 внутренние, то
внутренние, то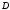 называетсяоткрытым множеством.
называетсяоткрытым множеством.
Определение 4. Точка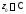 называетсяграничной точкой множества
называетсяграничной точкой множества
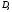 если в любой окрестности этой точки
имеются как точки, принадлежащие
если в любой окрестности этой точки
имеются как точки, принадлежащие так и точки, не принадлежащие
так и точки, не принадлежащие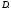 Множество всех граничных точек
Множество всех граничных точек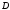 образуетграницу
образуетграницу
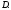 Обозначение:
Обозначение: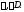
Определение 5. Множество
 называетсясвязным,если любые
две его точки можно соединить непрерывной
кривой, не выходя из
называетсясвязным,если любые
две его точки можно соединить непрерывной
кривой, не выходя из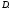 Множество
Множество
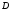 называетсяодносвязным,если
любой замкнутый контур, лежащий в
называетсяодносвязным,если
любой замкнутый контур, лежащий в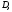 можно стянуть в точку, не выходя из
можно стянуть в точку, не выходя из И, наконец, множество
И, наконец, множество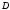 называется
называется связным,
если его граница
связным,
если его граница состоит из
состоит из попарно не пересекающихся между собой
замкнутых контуров.
попарно не пересекающихся между собой
замкнутых контуров.
Определение 6. Любое открытое
связное множество называетсяобластью.
Область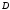 называетсяограниченной, если
существует круг, охватывающий область
называетсяограниченной, если
существует круг, охватывающий область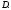 В противном случае область
В противном случае область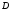 называетсяне ограниченной.
называетсяне ограниченной.
Пусть
 и
и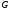 две области на комплексной плоскости
две области на комплексной плоскости причем
причем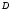 находится в плоскости
находится в плоскости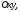 а
а в плоскости
в плоскости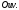
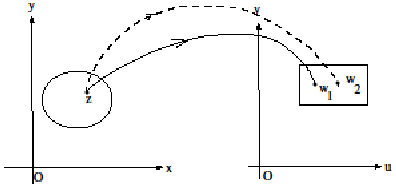
Определение 7.Говорят, что задана
функция отображающая область
отображающая область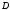 в область
в область если каждому числу
если каждому числу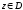 поставлено в соответствие одно или
несколько комплексных чисел
поставлено в соответствие одно или
несколько комплексных чисел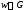 по закону
по закону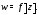 При этом
При этом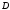 называетсяобластью определенияфункции
называетсяобластью определенияфункции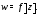 Если каждому
Если каждому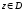 поставлено в соответствие единственное
число
поставлено в соответствие единственное
число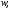 то говорят, что функция
то говорят, что функция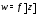 однозначна;
в противном случае функция
однозначна;
в противном случае функция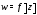 многозначна. Функция называетсяоднолистной в области
многозначна. Функция называетсяоднолистной в области если
если
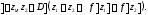
Например, функция
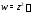 однозначная, но не однолистная, а функция
однозначная, но не однолистная, а функция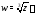 трёхзначная. Функция
трёхзначная. Функция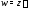 однозначная и однолистная.
однозначная и однолистная.
Поскольку каждое комплексное число
вполне определяется своей действительной
и мнимой частью, то функцию
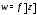 комплексной переменной можно записать
в виде
комплексной переменной можно записать
в виде
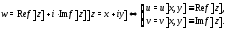
Например, функцию
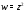 можно записать в указанном виде, если
в ней выделить действительную и мнимую
части:
можно записать в указанном виде, если
в ней выделить действительную и мнимую
части: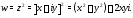 Здесь
Здесь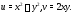 Частные типы комплексных функций:
Частные типы комплексных функций:
а) комплексная последовательность:
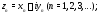
б) комплексная функция действительного
аргумента:

С последней функцией мы встречались в
главе 4 при рассмотрении комплексных
решений дифференциальных уравнений.
Такие функции часто используются при
задании кривых в комплексной плоскости.
Например, уравнение
 описывает уравнение окружности в
плоскости
описывает уравнение окружности в
плоскости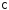 радиуса
радиуса и с центром в точке
и с центром в точке
