3. Дифференциальные уравнения с разделяющимися переменными. Однородные уравнения

Опишем теперь аналитические методы решения некоторых дифференциальных уравнений.

1. Уравнения с разделенными переменными:

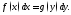
Ясно, что общий интеграл этого уравнения может быть получен интегрированием обеих частей (функции инепрерывны в своих областях определения):

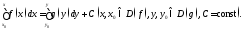
Отметим, что здесь часто вместо определённых интегралов пишут неопределённые.

2. Уравнения с разделяющимися переменными:

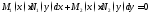
(здесь перед дифференциалами стоят произведения функций с разделёнными переменными).

Предполагая, что функции 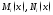непрерывныв своих областях определения, разделим обе части уравнения (4) на произведение будем иметь

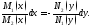
Получено уравнение с разделёнными переменными. Интегрируя его, получим общий интеграл

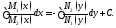
Однако это верно в случае, когда Случа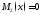иили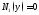надо рассматривать отдельно. Если при этом будут получены решения уравнения (4), то их надо присовокупить к уже полченным.

Пример 2. Решить уравнение

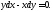
Решение. Разделяем переменные, поделив обе части уравнения на произведение

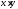
и интегрируем полученное уравнение:

Рассматриваем отдельно случа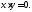й При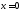исходное уравнение обращается в тождество, значит,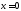– решение. Оно может быть получено изпри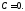Функция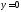также удовлетворяет данному уравнение. Однако она не может быть получена из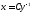. Следовательно, решениями исходного уравнения является совокупность функций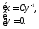

3. Однородные уравнения:

Такие уравнения приводятся к уравнению с разделяющимися переменной заменой гденовая неизвестная функция. Действительно, дифференцируя замену и подставляя её в исходное уравнение, будем иметь

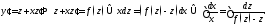
Заметим, что к однородным приводятся уравнения вида

В первом случае надо разделить числитель и знаменатель входящей под знак функции дроби на во втором случае сделать замену переменных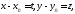где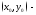решение системы уравнений

Пример 3. Решить уравнение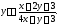

Решение. Найдем решение системы 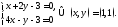Делаем замену переменных Вместо исходного получим следующее уравнение:

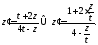jj

Это уравнение однородно, поэтому делаем замену 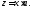В итоге получим уравнениерешая которое методом разделения переменных, будем иметь

Получен общий интеграл данного уравнения.

Лекция 2. Линейные уравнения первого порядка. Дифференциальные уравнения высшего порядка. Задача Коши. Теорема существования и единственности решения задачи Коши. Общее решение и общий интеграл. Методы понижения порядка дифференциального уравнения

Наиболее часто встречаются линейные дифференциальные уравнения. Так называются уравнения, у которых правая часть линейна относительно неизвестной функции. Перейдём к их рассмотрению.

1. Линейные дифференциальные уравнения. Метод вариации произвольной постоянной

Уравнение вида

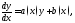
где 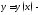неизвестная функция,известные функции², называетсялинейным дифференциальным уравнением. Если 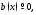то уравнение (1) называетсяоднородным. Если то (1) называютнеоднородным уравнением. Часто 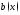называютсвободным членом уравнения (1) или неоднородностью.

Теорема 1. Пусть в уравнении (1) функции 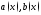непрерывны на отрезке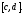Тогда уравнение (1) с начальным условием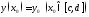имеет на отрезке

единственное решение и это решение может быть записано в виде

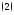
Доказательство. Найдем решение уравнения (1). Применим для этого так называемый метод вариации произвольной постоянной Лагранжа, который состоит в следующем.

Решим сначала однородное уравнение, соответствующее уравнению (1):

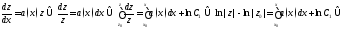
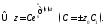Затем вычислим решение уравнения (1), варьируя постоянную в решении однородного уравнения, т.е. будем определять решение уравнения (1) в ви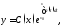дегде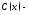неизвестная функция. Подставляя предполагаемое решение в уравнение (1), будем иметь

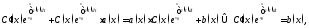
откуда находим 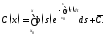Значит, общее решение уравнения (1) можно записать в виде

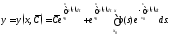
Подчиняя его начальному условию найдём, чтоСледовательно, решение уравнения (1) с начальным условием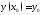имеет вид (2). Теорема доказана.

Замечание 1. Так как второе слагаемое в 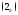есть частное решение (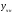) неоднород-

ного уравнения (1) (проверьте это!), а первое слагаемое суть общее решени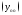е соответствующего однородного уравнения, то для линейных дифференциальных уравнений имеет место утверждение:общее решение неоднородного уравнения равно сумме общего решения соответствующего однородного уравнения и частного решения неоднородного уравнения, т.е.

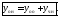
Замечание 2. В отличие от нелинейных уравнений, имеющих, как правило, локальные решения, линейные дифференциальные уравнения имеют “глобальные решения,” т.е. они существуют на отрезке на котором непрерывны коэффициенты уравнения (1).

И наконец, отметим, что так называемое уравнение Бернулли:

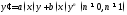
приводится к линейному уравнению делением обеих частей на 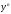и дальнейшей заменой переменной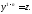

Пример 1 (Кузнецов Л.А. Типовые расчеты). Решить задачу Коши

Решение. Можно было бы сразу воспользоваться формулой (6), но мы ещё раз продемонстрируем метод Лагранжа. Найдём сначала общее решение соответствующего однородного уравнения:

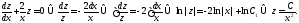
Вычисляя общее решение исходного уравнения в виде 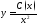, будем иметь

Значит, общим решением данного неоднородного уравнения является функция

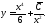Подчиняя её начальному условию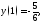будем иметьСледовательно, решением исходной задачи Коши будет функция

Если в уравнении 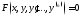порядокто это уравнение называютуравнением высшего порядка. Мы будем рассматривать уравнения высших порядков, разрешённые относительно старшей производной:

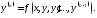
Областью определения уравнения (1) называется множество

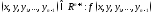{имеет смысл }.