- •3 Семестр (часть 1). Дифференциальные уравнения
- •1. Общие понятия
- •3. Дифференциальные уравнения с разделяющимися переменными. Однородные уравнения
- •1. Линейные дифференциальные уравнения. Метод вариации произвольной постоянной
- •2. Задача Коши. Теорема существования и единственности решения задачи Коши. Общее решение и общий интеграл
- •3. Уравнения, допускающие понижение порядка
- •1. Свойства дифференциального оператора. Теорема Коши
- •2. Линейная зависимость и линейная независимость системы функций. Вронскиан. Исследование линейной независимости с помощью вронскиана
- •3. Структура общего решения однородного дифференциального уравнения
- •Лекция 4. Общее решение неоднородного уравнения. Метод вариации произвольных постоянных Лагранжа. Комплексные решения дифференциальных уравнений. Построение фундаментальной системы решений
- •1. Структура общего решения неоднородного уравнения. Метод вариации произвольных постоянных Лагранжа
- •2.Метод вариации произвольных постоянных Лагранжа
- •3. Комплексные решения дифференциальных уравнений. Линейная независимость комплексных решений
- •Лекция 5. Линейные дифференциальные уравнения с постоянными коэффициентами. Метод Эйлера и метод подбора вычисления частных решений неоднородных уравнений
- •1. Метод Эйлера построения общего решения однородного дифференциального уравнения с постоянными коэффициентами в случае простых корней характеристического уравнения
- •2. Построение общего решения однородного дифференциального уравнения в случае кратных корней характеристического уравнения
- •3. Построение общего решения неоднородного уравнения с постоянными коэффициентами. Метод подбора частного решения неоднородного уравнения
- •Лекция 6. Комплексные числа и действия над ними. Функции комплексного переменного. Предел и непрерывность. Элементарные функции комплексного переменного и действия над ними
- •1. Извлечение корня й степени из комплексного числа. Множества в комплексной плоскости
- •2. Предел и непрерывность функции комплексной переменной
- •Лекция 7. Производная функции комплексного переменного. Аналитичность функции в точке и в области. Условия Коши-Римана. Элементарные аналитические функции
- •2. Геометрический смысл модуля и аргумента производной
- •Лекция 8 . Интеграл от функции комплексного переменного. Теорема Коши и для односвязной и многосвязной областей. Интегральная формула Коши. Существование всех производных для аналитической функции
- •2.2. Теорема Коши для односвязной области и многосвязной области. Интегральная формула Коши
- •3. Первообразная функции комплексных переменных
- •Лекция 9. Ряды в комплексной области. Степенные ряды. Теорема Абеля. Ряды Тейлора и Лорана
- •1. Степенные ряды. Ряды Тейлора и Лорана
- •Лекция 10. Изолированные особые точки. Ряды Лорана для функций, аналитических в кольце
- •1. Разложение функции в ряд Лорана
- •2. Нули аналитической функции и их связь с полюсами
- •3. Вычеты. Теорема Коши о вычетах
- •Лекция 11. Вычисление вычетов и применение теории вычетов для вычисления контурных и несобственных интегралов
- •1. Вычисление вычетов
- •2. Вычисление интегралов
- •Лекция 12. Преобразование Лапласа и его свойства. Применение к дифференциальным уравнениям
- •Лекция 13. Системы дифференциальных уравнений. Общие понятия
- •1. Понятия общего и частного решений. Задача Коши и ее разрешимость
- •2. Методы интегрирования систем дифференциальных уравнений
- •Лекция 14. Системы линейных дифференциальных уравнений
- •1. Глобальная теорема разрешимости начальной задачи для линейной системы дифференциальных уравнений
- •2. Линейная зависимость и линейная независимость системы произвольных вектор-функций и решений однородной системы уравнений
- •3. Фундаментальная матрица решений и структура общего решения однородной системы
- •4. Структура общего решения неоднородной системы дифференциальных уравнений
- •Лекция 15. Построение фундаментальной матрицы решений дифференциальной системы с постоянной матрицей. Метод Эйлера.
Лекция 12. Преобразование Лапласа и его свойства. Применение к дифференциальным уравнениям
Пусть функция
 является комплексной функцией
действительного аргумента
является комплексной функцией
действительного аргумента т.е.
т.е.
Определение 1.
Функция
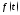 называетсяоригиналом,
если выполнены следующие условия:
называетсяоригиналом,
если выполнены следующие условия:
1.
 2.
2.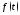 кусочно-непрерывна на любом конечном
отрезке
кусочно-непрерывна на любом конечном
отрезке 3. существуют постоянные
3. существуют постоянные и
и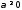 такие, что
такие, что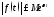
 При этом число5
При этом число5 называетсяпоказателем
роста (или индексом)
оригинала
называетсяпоказателем
роста (или индексом)
оригинала
 .
.
Например, функция Хевисайда (единичная функция):

является оригиналом
с показателем роста
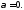 Заметим, что если функция
Заметим, что если функция удовлетворяет только условиям 2 и 3, то
функция
удовлетворяет только условиям 2 и 3, то
функция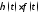 является оригиналом. По этой причине
множитель
является оригиналом. По этой причине
множитель в
в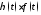 часто опускают и пишут просто
часто опускают и пишут просто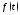 .
.
Определение 2.
Пусть
 –оригинал.
Функция
–оригинал.
Функция
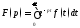 называется
преобразованием
Лапласа функции
называется
преобразованием
Лапласа функции
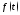 (другие
названия:
(другие
названия: изображение по Лапласу,
изображение по Лапласу, образ
преобразования Лапласа). При этом пишут
образ
преобразования Лапласа). При этом пишут

Теорема 1. Если
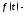 оригинал с показателем роста
оригинал с показателем роста то его изображение
то его изображение существует и аналитично в полуплоскости
существует и аналитично в полуплоскости При этом
При этом
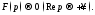
Доказательство. Имеем
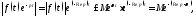
поэтому при
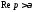 имеет место оценка
имеет место оценка
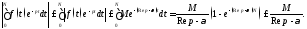
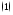
При
 отсюда получаем, что интеграл
отсюда получаем, что интеграл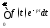 абсолютно сходится при всех
абсолютно сходится при всех и что имеет место оценка
и что имеет место оценка
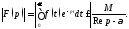
Устремляя здесь
 получим, что
получим, что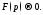
Итак, показано,
что преобразование Лапласа
 существует в
полуплоскости
существует в
полуплоскости
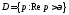 и что имеет место утверждение
и что имеет место утверждение
 Дифференцируя равенство
Дифференцируя равенство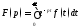 по параметру, покажем, что производная
по параметру, покажем, что производная
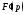 существует при всех
существует при всех
 Это означает, что
Это означает, что аналитична в области
аналитична в области Теорема доказана.
Теорема доказана.
Замечание 1.
Желая указать
показатель роста
 оригинала
оригинала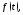 будем писать
будем писать

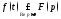 или
или
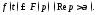
Теорема 2
(свойства
преобразования Лапласа). При указанных
значениях
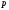 имеют место следующие утверждения (ниже
имеют место следующие утверждения (ниже и
и произвольные постоянные):
произвольные постоянные):
 (линейность).
(линейность).

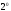 (теорема
подобия).
(теорема
подобия).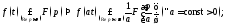
 (теорема запаздывания).
(теорема запаздывания).

 (теорема
смещения).
(теорема
смещения). 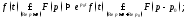
 (теорема о
дифференцировании оригинала). Если
(теорема о
дифференцировании оригинала). Если
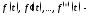 оригиналы с показателем роста
оригиналы с показателем роста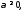 то
то

 (теорема
об интегрировании оригинала).
(теорема
об интегрировании оригинала).
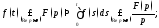
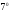 (теорема о
дифференцировании изображения).
(теорема о
дифференцировании изображения).

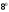 (теорема об
интегрировании изображения). Пусть
(теорема об
интегрировании изображения). Пусть
 и интеграл
и интеграл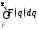 сходится. Тогда
сходится. Тогда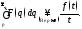
Определение 3.
Свёрткой
функций
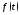 и
и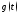 называется
интеграл
называется
интеграл

Очевидно, что
свёртка коммутативна, т.е.

 (теорема умножения).
(теорема умножения).
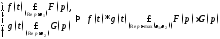 (здесь попутно утверждается, что свёртка
оригиналов также является оригиналом).
(здесь попутно утверждается, что свёртка
оригиналов также является оригиналом).
 (интеграл
Дюамеля). Если
(интеграл
Дюамеля). Если
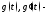 оригиналы
с показателем роста
оригиналы
с показателем роста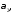 а
а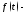 оригинал
с показателем роста
оригинал
с показателем роста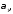 то
то
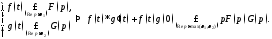
Все эти свойства
доказываются довольно просто. Докажем,
например, теорему о дифференцировании
оригинала. Имеем при

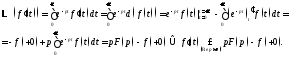
Мы показали
справедливость свойства
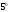 при
при Аналогично показывается его справедливость
при любом
Аналогично показывается его справедливость
при любом
Приведём теперь таблицу изображений основных функций.
Таблица 2. Преобразования Лапласа основных функций
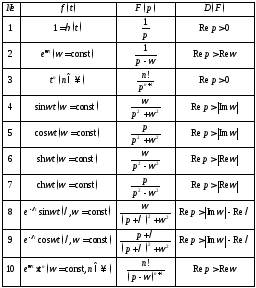
Все формулы этой
таблицы доказываются либо непосредственным
вычислением изображений, либо применением
свойств
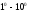 преобразования Лапласа. Покажем,
например, справедливость формулы 6.
Поскольку
преобразования Лапласа. Покажем,
например, справедливость формулы 6.
Поскольку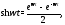 то формуле 2 и по свойству
то формуле 2 и по свойству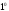 будем иметь
будем иметь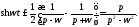 Это высказывание имеет место, если
одновременно
Это высказывание имеет место, если
одновременно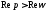 и
и т.е. если
т.е. если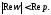 Формула 6
доказана.
Формула 6
доказана.
Рассмотрим несколько примеров.
Пример 1. Найти
изображения следующих функций: а)
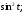 б)
б)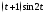
Решение. а) Воспользуемся формулой понижения порядка и формулами 1 и 5 таблицы 2:

б) Представим
функцию
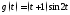 в виде
в виде По таблице 2 сразу же находим
По таблице 2 сразу же находим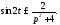 Осталось найти изображение функции
Осталось найти изображение функции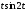 Воспользуемся для этого теоремой
Воспользуемся для этого теоремой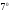 о дифференцировании
изображения:
о дифференцировании
изображения:
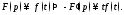
Так как в нашем
случае
 то
то Таким
образом,
Таким
образом,
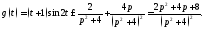
Пример 2. Найти
изображение функции
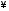

Решение. Можно
было бы сначала вычислить интеграл, а
затем найти изображение, но проще
воспользоваться теоремой об интегрировании оригинала
об интегрировании оригинала

В нашем случае

Пример 3. Найти
изображение функции
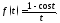
Решение.
Воспользуемся
теоремой
 об интегрировании
изображения:
об интегрировании
изображения:

Сначала найдём изображение функции
 Тогда будем иметь
Тогда будем иметь
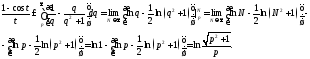
Пример 4. Найти
преобразование Лапласа функции
 изображённой на рисунке.
изображённой на рисунке.
Решение. Можно было бы применить теорему запаздывания, но проще вычислить изображение по определению:
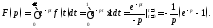
Следующее утверждение показывает, как можно восстановить оригинал по изображению.
Теорема
обращения Меллина. Пусть
аналитическая в области
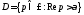 функция
функция является изображением некоторого
оригинала
является изображением некоторого
оригинала
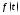 с
показателем роста
с
показателем роста
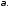 Тогда в каждой точке
Тогда в каждой точке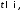 в которой
функция
в которой
функция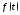 непрерывна,
имеет место равенство
непрерывна,
имеет место равенство

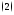
где
 произвольная
постоянная, удовлетворяющая неравенству
произвольная
постоянная, удовлетворяющая неравенству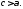
Из теоремы Меллина вытекает следующее утверждение об умножении оригиналов.
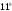 .
.
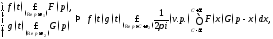
где
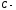 произвольная
постоянная, удовлетворяющая неравенству
произвольная
постоянная, удовлетворяющая неравенству
При использовании
теоремы Меллина возникают две основные
трудности. Первая из них заключается в
проверке того, что функция
 является оригиналом, вторая –
является оригиналом, вторая –
в вычислении самого интеграла Меллина (2). Поэтому обычно применяют более простые теоремы разложения, где эти трудности преодолеваются очевидным образом.
Первая теорема
обращения.
Пусть функция
 имеет в окрестности точки
имеет в окрестности точки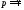 лорановское разложение вида
лорановское разложение вида сходящееся абсолютно при
сходящееся абсолютно при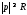
 некоторая постоянная
некоторая постоянная .
Тогда оригинал для
.
Тогда оригинал для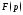 существует в области
существует в области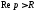 и имеет вид
и имеет вид
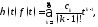

причем этот ряд
сходится абсолютно для всех
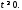
Вторая теорема
обращения.
Пусть функция
 правильная
дробь (т.е.
правильная
дробь (т.е. многочлены,
причем степень многочлена
многочлены,
причем степень многочлена меньше степени многочлена
меньше степени многочлена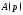 ).
Тогда для функции
).
Тогда для функции существует оригинал
существует оригинал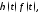 причем функция
причем функция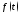 имеет вид
имеет вид
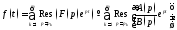

где вычеты
вычисляются по всем нулям
 знаменателя
знаменателя
 Пусть, например,
надо найти оригинал функции
Пусть, например,
надо найти оригинал функции
 Первый способ вычисления оригинала
основан на разложении
Первый способ вычисления оригинала
основан на разложении на простейшие дроби:
на простейшие дроби:
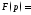

При этом оригинал
 находится по таблице 2 с использованием
свойства 10
линейности преобразования Лапласа. Из
той же таблицы находим, что изображение
находится по таблице 2 с использованием
свойства 10
линейности преобразования Лапласа. Из
той же таблицы находим, что изображение
 существует при
существует при Другой способ основан на второй теореме
разложения:
Другой способ основан на второй теореме
разложения:
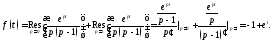
Покажем теперь, как применяется операционное исчисление к решению дифференциальных уравнений. Рассмотрим задачу Коши


с
постоянными коэффициентами
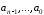 Предположим, что неоднородность
Предположим, что неоднородность и решение
и решение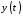 являются оригиналами, причем
являются оригиналами, причем Применяя теорему
Применяя теорему о дифференцировании оригинала, будем
иметь
о дифференцировании оригинала, будем
иметь

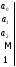

Умножая
эти равенства на соответствующие
коэффициенты
 стоящие слева от черты, и складывая
полученные результаты, будем иметь
стоящие слева от черты, и складывая
полученные результаты, будем иметь


где
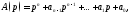 а
а многочлен
от
многочлен
от
 й
степени, коэффициенты которого зависят
лишь от начальных условий
й
степени, коэффициенты которого зависят
лишь от начальных условий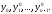 Правая часть (6) называется изображением
левой части уравнения (5) с учётом
соответствующих начальных условий.
Приравнивая его к изображению левой
части (5), получим алгебраическое уравнение
Правая часть (6) называется изображением
левой части уравнения (5) с учётом
соответствующих начальных условий.
Приравнивая его к изображению левой
части (5), получим алгебраическое уравнение


называемое
операторным
уравнением, соответствующим задаче
(5). Решением
этого уравнения является функция
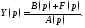 Получено изображение решения
Получено изображение решения задачи (5). Применяя
теорему Меллина, получим и само решение:
задачи (5). Применяя
теорему Меллина, получим и само решение:
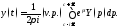
Замечание. Если
все начальные значения нулевые ( ),
то
),
то
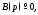 и операторное уравнение (7) будет иметь
более простое решение:
и операторное уравнение (7) будет иметь
более простое решение: Заметим также, что
Заметим также, что
 является характеристическим полиномом
уравнения (5).
является характеристическим полиномом
уравнения (5).
Пример 5. Решить
задачу Коши
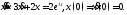
Решение.
Пусть
 Имеем
Имеем
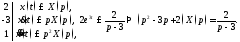
Из
последнего уравнения находим, что
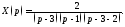 Находим теперь оригинал-решение исходной
задачи, разлагая изображение решения
на простейшие дроби и используя таблицу
2:
Находим теперь оригинал-решение исходной
задачи, разлагая изображение решения
на простейшие дроби и используя таблицу
2:
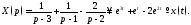
Задачу
вычисления уравнения (5) с нулевыми
начальными условиями и произвольной
неоднородностью
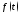 можно свести к решению той же задачи,
но с неоднородностью
можно свести к решению той же задачи,
но с неоднородностью Делается это с помощью следующего
свойства преобразования Лапласа:
Делается это с помощью следующего
свойства преобразования Лапласа:
 (интеграл
Дюамеля). Если
(интеграл
Дюамеля). Если
 оригиналы
с показателем роста
оригиналы
с показателем роста а
а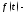 оригинал
с показателем роста
оригинал
с показателем роста то
то

Рассмотрим задачу
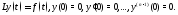
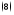
Чтобы решить её, рассмотрим вспомогательную задачу
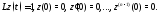
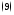
Покажем,
что если известно решение
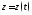 этой задачи, торешение
задачи (8) является свёрткой её
неоднородности с производной от решения
вспомогательной задачи (9):
этой задачи, торешение
задачи (8) является свёрткой её
неоднородности с производной от решения
вспомогательной задачи (9):
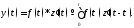

Действительно, формула
 с учетом того, что
с учетом того, что перепишется в виде
перепишется в виде где
где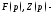 изображения функций
изображения функций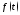 и
и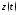 соответственно. Операторным решением
задачи (8) является функция
соответственно. Операторным решением
задачи (8) является функция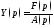 (см. замечание), а операторным решением
вспомогательной задачи (9) является
функция
(см. замечание), а операторным решением
вспомогательной задачи (9) является
функция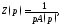 поэтому
поэтому Отсюда и из формулы
Отсюда и из формулы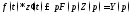 получаем, что
получаем, что т.е. имеет место формула (10).
т.е. имеет место формула (10).
Пример 6.Решить задачу Коши

Решение.Решим сначала вспомогательную
задачу Оператор-
Оператор-
ным
решением для неё будет функция
 Так как
Так как
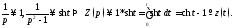
Решение же исходной задачи находим по формуле (10):