2. Методы интегрирования систем дифференциальных уравнений

Одним из методов решения систем дифференциальных уравнений является метод исключения, суть которого заключается в том, чтобы путем дифференцирования уравнений свести данную систему к одному дифференциальному уравнению высшего порядка. Рассмотрим этот метод на примерах.

Пример 2.Решить систему уравнений

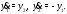
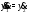Решение.Дифференцируя первое уравнение системы (6) пополучаем уравнениеПроизводную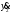заменяем на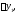используя второе уравнение (6). В результате имеем уравнение

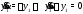
второго порядка относительно одной функции 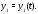Его характеристическое уравнение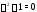имеет два различных чисто мнимых корняЗначит, общее решение имеет вид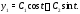Поскольку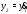(см. первое уравнение (6)), то вторая компонента решения системы (24.6) вычисляется по формуле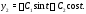Таким образом,

Пример 3.Решить систему уравнений

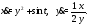
Решение.Дифференцируя первое уравнение системы (7), будем иметь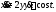Из второго уравнения (7) находим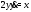и подставляем в последнее уравнение. В результате будем иметь

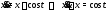
Это линейное уравнение второго порядка. Его общее решение вычисляем, например, методом подбора. Оно будет иметь вид

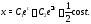
Из первого уравнения системы (7) находим

Следовательно,

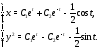
Заметим, что в последнем примере решение записано в виде интеграла.

Вторым способом решения систем уравнений является метод интегрируемых комбинаций. Суть этого метода состоит в том, чтобы подходящими преобразованиями привести исходную систему к одному дифференциальному уравнению относительно некоторой функции компонент данной системы. Если это уравнение легко интегрируется, то говорят, что оно является интегрируемой комбинацией данной системы. Получив достаточное число интегрируемых комбинаций, а затем рассмотрев их совместно, можно найти решение данной системы.

Пример 4.Решить систему уравнений

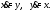
Решение.Эту систему можно было бы решить методом исключения. Однако попробуем найти ее решение методом интегрируемых комбинаций. Складывая почленно оба уравнения (8), получаем интегрируемую комбинацию

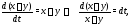
откуда вычисляем 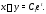Вычитая из первого уравнения системы (8) ее второе уравнение, получаем еще одну интегрируемую комбинацию

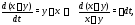
из которой находим 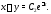Итак, получено два алгебраических уравнения

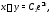
из которых легко находим решение системы (8):

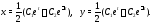
Соотношени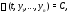е где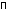– скалярная функция,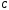– постоянная, называется первым интегралом системы (1), если при подстановке в него решения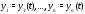оно обращается в тождество. Часто первым интегралом системы (1) называют скалярную функцию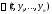, сохраняющую постоянное значение на решениях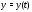системы (1).

Ясно, что одна интегрируемая комбинация системы (1) позволяет выписать один первый интеграл этой системы. Если найдено интегрируемых комбинаций, то получимпервых интегралов

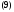
Если при этом определитель

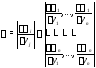
не равен нулю в области 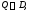то (9) задают общий интеграл (в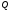) системы (1). Это означает, что система алгебраических уравнений (9) задает общее решение дифференциальной системы (1) в неявной форме. Заметим, что определительназывается якобианомсистемы функций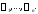Если якобианне равен нулю в области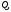то система функций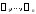будет функционально независимой в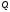В этом случае система уравнений (9) может быть разрешена относительно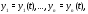причем однозначно.