Лекция 14. Системы линейных дифференциальных уравнений

Если в дифференциальной системе 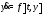правая часть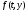линейна по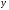, то эта система называется линейной системой дифференциальных уравнений. Такая система имеет вид

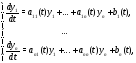
где 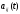и– известные функции,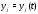– неизвестные функции (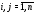). Пользуясь векторно-матричными обозначениями, систему (1) можно записать в следующей компактной форме:

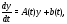
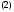
где

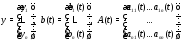
Мы будем пользоваться преимущественно записью (2). При этом число компонент неизвестной вектор-функции 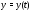(или размерность матрицы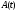) называется порядкомсистемы (2). Таким образом, (2) – дифференциальная система-го порядка.

Вектор-функция называется неоднородностью системы (2). Если(т.е. если все компоненты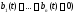, то система (2) называется однородной; в противном случае (т.е. если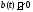) система (2) называется неоднородной системой. Если в (2) отбросить неоднородность, то получим соответствующую ей однородную систему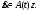

Оператор 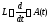позволяет записать систему (2) кратко так: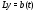. Изучим свойства этого оператора. Будем обозначать через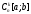пространство-мерных вектор-функций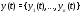, непрерывных на отрезке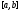вместе с производными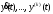до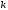-го порядка включительно (часто индексв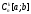опускают, если из контекста ясно, о каких вектор-функциях идет речь). Имеют место следующие утверждения.

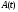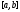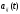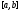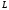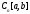Если матрицанепрерывна на отрезке(т.е. если все ее элементынепрерывны на), то оператордействует из пространствав пространствонепрерывных на отрезке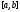вектор-функций:

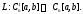
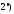Операторлинеен, т.е.

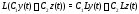
для произвольных чисел ии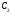 произвольных элементови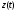пространства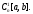

Первое свойство вытекает из того, что при дифференцировании гладкость функции понижается на единицу, а второе свойство вытекает из того, что операторы 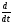и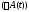являются линейными операторами, а значит линейным оператором является и их сумма.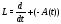

Если через обозначить пространство решений однородной системы уравненийc непрерывной матрицей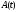, то из свойств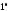и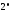сразу же вытекает, что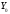– линейное пространство. Как и в случае скалярных дифференциальных уравнений, нас будет интересовать, какова размерность пространства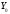и какие системы функций образуют в нем базис. Мы ответим на эти вопросы, если научимся выделять в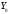максимальную линейно независимую систему элементов.

1. Глобальная теорема разрешимости начальной задачи для линейной системы дифференциальных уравнений

Пусть 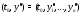– фиксированный постоянный вектор в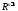. Рассмот-

рим начальную задачу

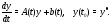
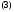
Имеет место следующее утверждение.

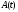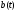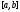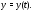Теорема 1. Если в системе (2) матрица и вектор-функциянепрерывны на отрезке, то какова бы ни была начальная точка, задача Коши (3) имеет решениеЭто решение единственно и определено на отрезке.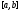

Таким образом, в случае линейной системы дифференциальных уравнений разрешимость начальной задачи глобальная: решение существует там, где непрерывна правая часть дифференциальной системы. В случае нелинейных систем это не так.

Пример 1.Показать, что задача Коши

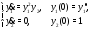
с непрерывными (при всех 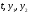) правыми частями не имеет решение, определенное при всехесли.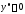

Решение.Из второго уравнения (4) находим, что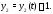Поэтому первое уравнение приобретает вид

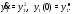
Разделяя здесь переменные, будем иметь

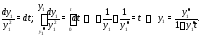
Итак, задача Коши (4) имеет следующее решение:

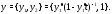
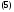
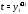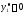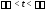Это решение единственно, так как выполнены все условия теоремы Коши. Первая компонента решения разрывна при (), поэтому каково бы ни было начальное значение, решение (5) не может существовать на всей оси, так как оно всегда разрывно в точке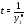.