- •3 Семестр (часть 1). Дифференциальные уравнения
- •1. Общие понятия
- •3. Дифференциальные уравнения с разделяющимися переменными. Однородные уравнения
- •1. Линейные дифференциальные уравнения. Метод вариации произвольной постоянной
- •2. Задача Коши. Теорема существования и единственности решения задачи Коши. Общее решение и общий интеграл
- •3. Уравнения, допускающие понижение порядка
- •1. Свойства дифференциального оператора. Теорема Коши
- •2. Линейная зависимость и линейная независимость системы функций. Вронскиан. Исследование линейной независимости с помощью вронскиана
- •3. Структура общего решения однородного дифференциального уравнения
- •Лекция 4. Общее решение неоднородного уравнения. Метод вариации произвольных постоянных Лагранжа. Комплексные решения дифференциальных уравнений. Построение фундаментальной системы решений
- •1. Структура общего решения неоднородного уравнения. Метод вариации произвольных постоянных Лагранжа
- •2.Метод вариации произвольных постоянных Лагранжа
- •3. Комплексные решения дифференциальных уравнений. Линейная независимость комплексных решений
- •Лекция 5. Линейные дифференциальные уравнения с постоянными коэффициентами. Метод Эйлера и метод подбора вычисления частных решений неоднородных уравнений
- •1. Метод Эйлера построения общего решения однородного дифференциального уравнения с постоянными коэффициентами в случае простых корней характеристического уравнения
- •2. Построение общего решения однородного дифференциального уравнения в случае кратных корней характеристического уравнения
- •3. Построение общего решения неоднородного уравнения с постоянными коэффициентами. Метод подбора частного решения неоднородного уравнения
- •Лекция 6. Комплексные числа и действия над ними. Функции комплексного переменного. Предел и непрерывность. Элементарные функции комплексного переменного и действия над ними
- •1. Извлечение корня й степени из комплексного числа. Множества в комплексной плоскости
- •2. Предел и непрерывность функции комплексной переменной
- •Лекция 7. Производная функции комплексного переменного. Аналитичность функции в точке и в области. Условия Коши-Римана. Элементарные аналитические функции
- •2. Геометрический смысл модуля и аргумента производной
- •Лекция 8 . Интеграл от функции комплексного переменного. Теорема Коши и для односвязной и многосвязной областей. Интегральная формула Коши. Существование всех производных для аналитической функции
- •2.2. Теорема Коши для односвязной области и многосвязной области. Интегральная формула Коши
- •3. Первообразная функции комплексных переменных
- •Лекция 9. Ряды в комплексной области. Степенные ряды. Теорема Абеля. Ряды Тейлора и Лорана
- •1. Степенные ряды. Ряды Тейлора и Лорана
- •Лекция 10. Изолированные особые точки. Ряды Лорана для функций, аналитических в кольце
- •1. Разложение функции в ряд Лорана
- •2. Нули аналитической функции и их связь с полюсами
- •3. Вычеты. Теорема Коши о вычетах
- •Лекция 11. Вычисление вычетов и применение теории вычетов для вычисления контурных и несобственных интегралов
- •1. Вычисление вычетов
- •2. Вычисление интегралов
- •Лекция 12. Преобразование Лапласа и его свойства. Применение к дифференциальным уравнениям
- •Лекция 13. Системы дифференциальных уравнений. Общие понятия
- •1. Понятия общего и частного решений. Задача Коши и ее разрешимость
- •2. Методы интегрирования систем дифференциальных уравнений
- •Лекция 14. Системы линейных дифференциальных уравнений
- •1. Глобальная теорема разрешимости начальной задачи для линейной системы дифференциальных уравнений
- •2. Линейная зависимость и линейная независимость системы произвольных вектор-функций и решений однородной системы уравнений
- •3. Фундаментальная матрица решений и структура общего решения однородной системы
- •4. Структура общего решения неоднородной системы дифференциальных уравнений
- •Лекция 15. Построение фундаментальной матрицы решений дифференциальной системы с постоянной матрицей. Метод Эйлера.
2. Линейная зависимость и линейная независимость системы произвольных вектор-функций и решений однородной системы уравнений
Эти понятия встречались при изучении скалярных дифференциальных уравнений. На вектор-функции они обобщаются следующим образом.
Определение 3.Система вектор-функций
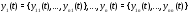
называется линейно зависимой на
отрезке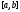 ,
если существуют числа
,
если существуют числа ,
не равные нулю одновременно, такие, что
для всех
,
не равные нулю одновременно, такие, что
для всех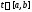 имеет место тождество
имеет место тождество
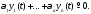
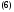
Если же тождество (6), где
 – числа, имеет место тогда и только
тогда, когда все
– числа, имеет место тогда и только
тогда, когда все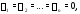 то система вектор-функций
то система вектор-функций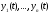 называетсялинейно независимой на
отрезке
называетсялинейно независимой на
отрезке
 .
.
Заметим, что векторное тождество (6)
эквивалентно
 скалярным тождествам
скалярным тождествам
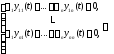

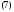
Определение 4.Определитель
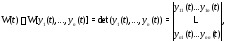
столбцами которого являются вектор-функции
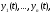 называется определителем Вронского
(или вронскианом) системы вектор-функций
называется определителем Вронского
(или вронскианом) системы вектор-функций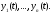
Теорема 2 (необходимое условие
линейной зависимости). Если система
вектор-функций
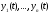 линейно зависима на отрезке
линейно зависима на отрезке ,
то их вронскиан
,
то их вронскиан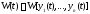 тождественно обращается в нуль на этом
отрезке, т.е.
тождественно обращается в нуль на этом
отрезке, т.е.
 .
.
Доказательство.Так как
вектор-функции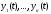 линейно зависимы на отрезке
линейно зависимы на отрезке ,
то существуют числа
,
то существуют числа ,
не равные нулю одновременно, такие, что
имеет место тождество (6). Но это означает,
что эквивалентная им линейная система
(7) алгебраических уравнений имеет при
всех
,
не равные нулю одновременно, такие, что
имеет место тождество (6). Но это означает,
что эквивалентная им линейная система
(7) алгебраических уравнений имеет при
всех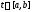 нетривиальное решение
нетривиальное решение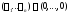 .
Это возможно лишь в том случае, когда
определитель системы (7) обращается в
нуль при всех
.
Это возможно лишь в том случае, когда
определитель системы (7) обращается в
нуль при всех .
Остается заметить, что указанный
определитель совпадает с вронскианом
системы функций
.
Остается заметить, что указанный
определитель совпадает с вронскианом
системы функций .
Теорема доказана.
.
Теорема доказана.
Следствие 1.Если вронскиан
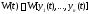 не обращается в нуль хотя бы в одной
точке
не обращается в нуль хотя бы в одной
точке ,
то система вектор-функций
,
то система вектор-функций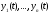 линейно независима на отрезке
линейно независима на отрезке (если, конечно, она имеет смысл на этом
отрезке).
(если, конечно, она имеет смысл на этом
отрезке).
Как и в скалярном случае, из тождества
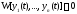 еще не следует, что система вектор-функций
еще не следует, что система вектор-функций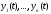 линейно зависима на отрезке
линейно зависима на отрезке Например, вектор-функции
Например, вектор-функции

линейно независимы на любом отрезке
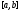 (докажите это!), а их вронскиан
(докажите это!), а их вронскиан
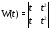
тождественно равен нулю на отрезке
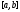 .
Однако для системы решений однородной
системы
.
Однако для системы решений однородной
системы


с непрерывной на отрезке
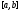 матрицей теорему 2 можно обратить.
матрицей теорему 2 можно обратить.
Теорема 3. Пусть
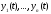 – система решений однородной
дифференциальной системы (8) с непрерывной
на отрезке
– система решений однородной
дифференциальной системы (8) с непрерывной
на отрезке матрицей
матрицей .
Тогда имеют место следующие утверждения:
.
Тогда имеют место следующие утверждения:
1) решения
 линейно независимы на отрезке
линейно независимы на отрезке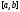 тогда и только тогда, когда их вронскиан
тогда и только тогда, когда их вронскиан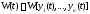 нe обращается в нуль ни в одной точке
отрезка
нe обращается в нуль ни в одной точке
отрезка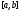 ;
;
2) решения
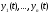 линейно зависимы на отрезке
линейно зависимы на отрезке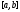 тогда и только тогда, когда их вронскиан
тогда и только тогда, когда их вронскиан тождественно равен нулю на отрезке
тождественно равен нулю на отрезке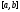 .
.
Докажем, например, утверждение 1).
Достаточность его очевидна, так как
если
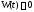 хотя бы в одной точке
хотя бы в одной точке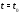 отрезка
отрезка ,
то из следствия 1 вытекает, что функции
,
то из следствия 1 вытекает, что функции линейно независимы на отрезке
линейно независимы на отрезке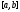 .
Докажем необходимость.
.
Докажем необходимость.
Пусть решения
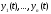 системы (8) линейно независимы на отрезке
системы (8) линейно независимы на отрезке .
Предположим, что существует точка
.
Предположим, что существует точка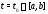 такая, что
такая, что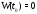 .
Отсюда следует, что столбцы
.
Отсюда следует, что столбцы определителя
определителя линейно зависимы, т.е. существуют числа
линейно зависимы, т.е. существуют числа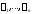 ,
не равные нулю одновременно, такие что
,
не равные нулю одновременно, такие что
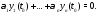

Рассмотрим вектор-функцию
 В силу линейности пространства
В силу линейности пространства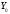 решений однородной системы (8) эта функция
является решением указанной дифференциальной
системы. Из (9) следует, что она удовлетворяет
начальному условию
решений однородной системы (8) эта функция
является решением указанной дифференциальной
системы. Из (9) следует, что она удовлетворяет
начальному условию Но такому же начальному условию
удовлетворяет и тривиальное решение
Но такому же начальному условию
удовлетворяет и тривиальное решение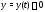 системы (8). В силу единственности решения
вектор-функции
системы (8). В силу единственности решения
вектор-функции и
и совпадают на отрезке
совпадают на отрезке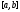 ,
т.е.
,
т.е.
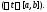 Следовательно,
Следовательно,
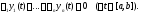
Поскольку здесь числа
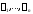 не равны нулю одновременно, то это
означает, что решения
не равны нулю одновременно, то это
означает, что решения линейно зависимы на отрезке
линейно зависимы на отрезке ,
чего не может быть. Значит, равенство
,
чего не может быть. Значит, равенство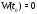 ложно, поэтому
ложно, поэтому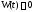 при всех
при всех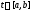 .
Теорема доказана.
.
Теорема доказана.
Из этой теоремы вытекают следующие
свойства вронскиана
 системы решений
системы решений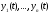 однородной диффернциальной системы
(8) с непрерывной на отрезке
однородной диффернциальной системы
(8) с непрерывной на отрезке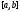 матрицей
матрицей :
:
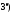 если вронскиан
если вронскиан
 обращается в нуль хотя бы в одной точке
обращается в нуль хотя бы в одной точке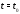 отрезка
отрезка ,
то
,
то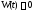
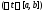 ;
;
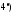 если вронскиан
если вронскиан
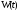 не равен нулю хотя бы в одной точке
не равен нулю хотя бы в одной точке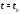 отрезка
отрезка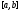 ,
то он не равен нулю на всем отрезке
,
то он не равен нулю на всем отрезке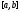 .
.
Эти свойства становятся очевидными, если воспользоваться формулой Лиувилля
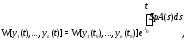
где
 – решения однородной системы (8) с
непрерывной на отрезке
– решения однородной системы (8) с
непрерывной на отрезке матрицей
матрицей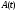 ,
а
,
а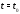 – произвольная фиксированная точка
этого отрезка. Через
– произвольная фиксированная точка
этого отрезка. Через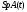 обозначен след матрицы
обозначен след матрицы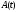 ,
т.е. сумма всех ее элементов
,
т.е. сумма всех ее элементов ,
стоящих на главной диагонали:
,
стоящих на главной диагонали: