1. Степенные ряды. Ряды Тейлора и Лорана

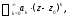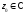Функциональные ряды вида где(коэффициенты ряда) и(центр ряда) – постоянные,переменная, называютсястепенными рядами.Ясно, что если мы научимся вычислять область сходимости степенного ряда

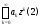
(с центром 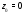), то легко найдем и область сходимости исходного ряда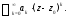Поэтому впредь, если не оговорено противное, будем рассматривать степенные ряды.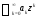

Теорема Абеля. Если степенной ряд 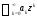сходится в точке 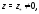то он сходится абсолютно и в круге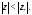В любом замкнутом круге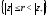указанный ряд сходится равномерно.

Так же, как и в действительном анализе, здесь вводится понятие радиуса сходимости ряда.

Определение 2.Число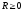называетсярадиусом сходимостиряда (2), если внутри круга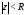этот ряд сходитсяабсолютно, а вне замкнутого круга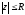он расходится. При этом круг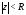называетсякругом сходимостиряда.

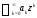Заметим, что при 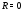указанный степенной ряд сходится только в точкеа при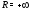он сходится при всех комплексныхСледующие примеры показывают, что эти случаи не исключаются: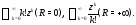Примером ряда с ненулевым конечным радиусом сходимости может служить геометрическая прогрессия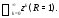Заметим также, что на границе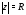круга сходимости степенной ряд может как сходиться, так и расходиться. Например, ряд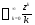сходится условно в точке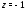и расходится в точке

Здесь так же, как и в действительном анализе имеет место утверждение.

Теорема 1. Пусть выполнено хотя бы одно из следующих условий:

а) существует (конечный или бесконечный) предел

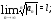
б) существует (конечный или бесконечный) предел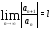(при этом предполагается, что существует номер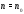такой, что).

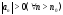Тогда число 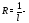радиус сходимости ряда.

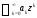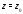Пусть функция имеет в точкеи некоторой её окрестности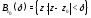производные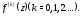Тогда этой функции можно поставить в соответствие степенной ряд

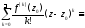
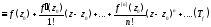
Этот ряд называется рядом Тейлора, построенным по функции 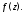Возникают следующие естественные вопросы:

1) при каких условиях на функцию 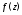ряд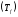сходится и какова область его сходимости?

2) при каких условиях на функцию 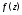ряд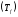сходится именно к функции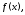по которой он строится?

На первый вопрос можно ответить, применяя к 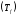признаки сходимости степенных

рядов. Ответ на второй вопрос содержится в следующем утверждении.

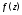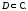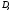Теорема 2(о разложимости аналитической функции в ряд Тейлора). Пусть функция аналитична в областиТогда в любом кругележащем в областифункция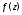разлагается в степенной ряд

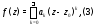
абсолютно сходящийся в круге 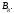Этот ряд необходимо является рядом Тейлора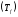

для функции 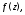т.е.

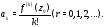
Таким образом, разложение аналитической функции в степенной ряд единственно.

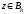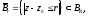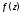Доказательство.Возьмём произвольно точкуи опишем кругохватывающий точкуТак как функцияаналитична в односвязной области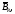то для неё справедлива интегральная формула Коши:

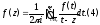
Преобразуем подынтегральное выражение следующим образом:

=[выносим за скобку вектор максимальной длины: ]=

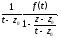=Так как

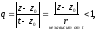
то геометрическая прогрессия

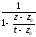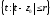разлагается в равномерно сходящийся в кругестепенной ряд

Поэтому

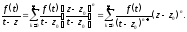
Подставляя это в (4), будем иметь

Учитывая, что

получаем утверждение нашей теоремы.

Для комплексных функций имеют место стандартные разложения в степенные ряды.

Таблица 1. Разложения основных элементарных функций в степенные ряды