
- •3 Семестр (часть 1). Дифференциальные уравнения
- •1. Общие понятия
- •3. Дифференциальные уравнения с разделяющимися переменными. Однородные уравнения
- •1. Линейные дифференциальные уравнения. Метод вариации произвольной постоянной
- •2. Задача Коши. Теорема существования и единственности решения задачи Коши. Общее решение и общий интеграл
- •3. Уравнения, допускающие понижение порядка
- •1. Свойства дифференциального оператора. Теорема Коши
- •2. Линейная зависимость и линейная независимость системы функций. Вронскиан. Исследование линейной независимости с помощью вронскиана
- •3. Структура общего решения однородного дифференциального уравнения
- •Лекция 4. Общее решение неоднородного уравнения. Метод вариации произвольных постоянных Лагранжа. Комплексные решения дифференциальных уравнений. Построение фундаментальной системы решений
- •1. Структура общего решения неоднородного уравнения. Метод вариации произвольных постоянных Лагранжа
- •2.Метод вариации произвольных постоянных Лагранжа
- •3. Комплексные решения дифференциальных уравнений. Линейная независимость комплексных решений
- •Лекция 5. Линейные дифференциальные уравнения с постоянными коэффициентами. Метод Эйлера и метод подбора вычисления частных решений неоднородных уравнений
- •1. Метод Эйлера построения общего решения однородного дифференциального уравнения с постоянными коэффициентами в случае простых корней характеристического уравнения
- •2. Построение общего решения однородного дифференциального уравнения в случае кратных корней характеристического уравнения
- •3. Построение общего решения неоднородного уравнения с постоянными коэффициентами. Метод подбора частного решения неоднородного уравнения
- •Лекция 6. Комплексные числа и действия над ними. Функции комплексного переменного. Предел и непрерывность. Элементарные функции комплексного переменного и действия над ними
- •1. Извлечение корня й степени из комплексного числа. Множества в комплексной плоскости
- •2. Предел и непрерывность функции комплексной переменной
- •Лекция 7. Производная функции комплексного переменного. Аналитичность функции в точке и в области. Условия Коши-Римана. Элементарные аналитические функции
- •2. Геометрический смысл модуля и аргумента производной
- •Лекция 8 . Интеграл от функции комплексного переменного. Теорема Коши и для односвязной и многосвязной областей. Интегральная формула Коши. Существование всех производных для аналитической функции
- •2.2. Теорема Коши для односвязной области и многосвязной области. Интегральная формула Коши
- •3. Первообразная функции комплексных переменных
- •Лекция 9. Ряды в комплексной области. Степенные ряды. Теорема Абеля. Ряды Тейлора и Лорана
- •1. Степенные ряды. Ряды Тейлора и Лорана
- •Лекция 10. Изолированные особые точки. Ряды Лорана для функций, аналитических в кольце
- •1. Разложение функции в ряд Лорана
- •2. Нули аналитической функции и их связь с полюсами
- •3. Вычеты. Теорема Коши о вычетах
- •Лекция 11. Вычисление вычетов и применение теории вычетов для вычисления контурных и несобственных интегралов
- •1. Вычисление вычетов
- •2. Вычисление интегралов
- •Лекция 12. Преобразование Лапласа и его свойства. Применение к дифференциальным уравнениям
- •Лекция 13. Системы дифференциальных уравнений. Общие понятия
- •1. Понятия общего и частного решений. Задача Коши и ее разрешимость
- •2. Методы интегрирования систем дифференциальных уравнений
- •Лекция 14. Системы линейных дифференциальных уравнений
- •1. Глобальная теорема разрешимости начальной задачи для линейной системы дифференциальных уравнений
- •2. Линейная зависимость и линейная независимость системы произвольных вектор-функций и решений однородной системы уравнений
- •3. Фундаментальная матрица решений и структура общего решения однородной системы
- •4. Структура общего решения неоднородной системы дифференциальных уравнений
- •Лекция 15. Построение фундаментальной матрицы решений дифференциальной системы с постоянной матрицей. Метод Эйлера.
Лекция 13. Системы дифференциальных уравнений. Общие понятия
Совокупность двух или более
дифференциальных уравнений называется
системой дифференциальных уравнений.
Примеры таких систем приводились в
лекции 1. Заметим, что в случае систем
обычно обозначают независимую переменную
буквой ,
рассматривая ее как время. Например,
уравнения
,
рассматривая ее как время. Например,
уравнения
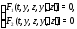
образуют систему двух уравнений с двумя
неизвестными функциями
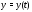 и
и .
Если система записана в виде уравнений
.
Если система записана в виде уравнений
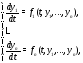
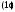
то ее называют системой, разрешенной
относительно всех производных, или
системой уравнений в нормальной форме.
Вводя в рассмотрение векторы
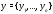 и
и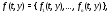 то систему
то систему можно записать кратко так:
можно записать кратко так:
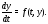
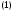
Такая форма записи системы уравнений
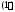 называется ее векторной формой. Ею мы
и будем пользоваться в дальнейшем.
называется ее векторной формой. Ею мы
и будем пользоваться в дальнейшем.
1. Понятия общего и частного решений. Задача Коши и ее разрешимость
Областью определения системы (1) называется
область определения ее правой части
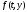 ,
т.е. множество
,
т.е. множество

Например, областью определения системы
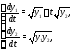
является множество
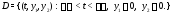
В левой части системы (1) стоит
производная вектор-функции
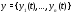 скалярного аргумента
скалярного аргумента .
В дальнейшем будут встречаться и
интегралы от вектор-функции. Поэтому с
самого начала разъясним соответствующие
понятия.
.
В дальнейшем будут встречаться и
интегралы от вектор-функции. Поэтому с
самого начала разъясним соответствующие
понятия.
Производная (любого порядка) вектор-функции скалярного аргумента определяется равенствами:
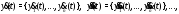
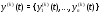
(здесь
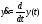 ),
а интеграл – равенством
),
а интеграл – равенством

Таким образом, чтобы продифференцировать
или проинтегрировать вектор-функцию
скалярного аргумента, надо продифференцировать
или проинтегрировать каждую компоненту
этой функции. Вектор-функция называется
непрерывной в точке
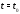 (или на множестве
(или на множестве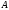 ),
если непрерывна в этой точке (или на
множестве
),
если непрерывна в этой точке (или на
множестве )
каждая компонента этой функции. Для
вектор-функций скалярного аргумента
сохраняются обычные правила
дифференцирования:
)
каждая компонента этой функции. Для
вектор-функций скалярного аргумента
сохраняются обычные правила
дифференцирования:
а)
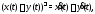
б)
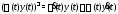 (
(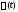 – скалярная функция),
– скалярная функция),
в)
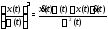 (
(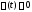 – скалярная функция),
– скалярная функция),
г)
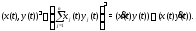
Интеграл от вектор-функции обладает свойствами линейности, аддитивности, дифференцируемости по верхнему и нижнему пределам. Например,
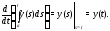
Имеет место оценка

где
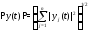 или
или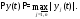
Если производную от матрицы
 определить равенством
определить равенством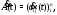 то, как нетрудно видеть, будут иметь
место формулы
то, как нетрудно видеть, будут иметь
место формулы
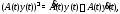

Перейдем к понятию решения системы (1).
Пусть
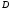 – область определения системы (1).
– область определения системы (1).
Определение 1.Решением системы
дифференциальных уравнений (1) на отрезке
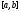 называется вектор-функция
называется вектор-функция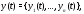 обладающая свойствами:
обладающая свойствами:
1)
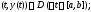
2) вектор-функция
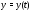 дифференцируема на отрезке
дифференцируема на отрезке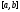 ;
;
3) при всех
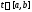 выполняется тождество
выполняется тождество
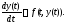
Аналогично определяются решения на
промежутках
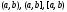 и
и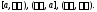 Если
Если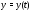 – решение системы (1) на отрезке
– решение системы (1) на отрезке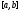 ,
то множество точек
,
то множество точек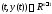 ,
когда
,
когда пробегает отрезок
пробегает отрезок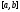 ,
образует в
,
образует в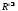 некоторую
некоторую Эту кривую называют интегральной
кривойсистемы (1). Пространство
Эту кривую называют интегральной
кривойсистемы (1). Пространство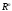 переменных
переменных называют фазовым пространством.
Проекция интегральной кривой
называют фазовым пространством.
Проекция интегральной кривой в фазовое пространство называется
траекториейсистемы уравнений (1).
Ясно, что по интегральной кривой
в фазовое пространство называется
траекториейсистемы уравнений (1).
Ясно, что по интегральной кривой траектория определяется однозначно,
но не наоборот. Впредь решение
траектория определяется однозначно,
но не наоборот. Впредь решение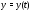 также будем называть интегральной
кривой системы (1).
также будем называть интегральной
кривой системы (1).
Мы знаем, что решение дифференциальных
уравнений определяется неоднозначно.
Чтобы выделить вполне конкретное
решение, надо задать дополнительные
условия. Пусть
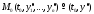 – фиксированная точка в области
– фиксированная точка в области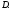 Задача, состоящая в нахождении решения
Задача, состоящая в нахождении решения системы (1), удовлетворяющего начальному
условию
системы (1), удовлетворяющего начальному
условию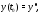 называется задачей Коши или начальной
задачейдля системы (1). Ее кратко Рис.
11 записывают так:
называется задачей Коши или начальной
задачейдля системы (1). Ее кратко Рис.
11 записывают так: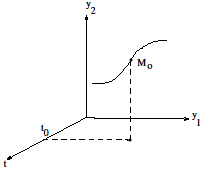
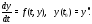
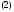
Ее геометрический смысл состоит в том,
чтобы среди всех интегральных кривых
системы (1) найти ту, которая проходит
через заданную начальную точку
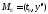 (см. рис. 11).
(см. рис. 11).
В каком случае задача Коши (2) имеет решение? Как и в случае скалярных дифференциальных уравнений это зависит от свойств правой части
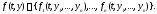
Теорема Коши. Пусть все
компоненты
 правой части
правой части и их частные производные
и их частные производные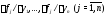 непрерывны в области
непрерывны в области .
Тогда какова бы ни была начальная точка
.
Тогда какова бы ни была начальная точка ,
лежащая внутри области
,
лежащая внутри области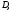 существует отрезок
существует отрезок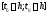 такой, что задача Коши (2) имеет решение
на этом отрезке, причем это решение
единственно.
такой, что задача Коши (2) имеет решение
на этом отрезке, причем это решение
единственно.
Отметим, что эта теорема носит
локальный характер: существование
решения
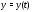 гарантируется лишь в достаточно малой
окрестности точки
гарантируется лишь в достаточно малой
окрестности точки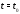 (
(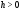 – достаточно мало). Кроме того, условия
этой теоремы носят достаточный характер.
При нарушении этих условий задача (2)
может иметь или может не иметь решения.
При этом, если решение существует, оно
может быть не единственным. Например,
задача Коши
– достаточно мало). Кроме того, условия
этой теоремы носят достаточный характер.
При нарушении этих условий задача (2)
может иметь или может не иметь решения.
При этом, если решение существует, оно
может быть не единственным. Например,
задача Коши

имеет два решения:
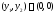 и
и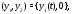 где
где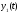 – функция вида
– функция вида
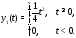
Нарушение единственности решения
объясняется тем, что условия теоремы
Коши здесь не выполнены (именно: частная
производная
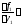
 разрывна в начальной точке
разрывна в начальной точке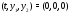 ).
).
Как и в случае скалярных уравнений,
здесь также вводятся понятия частного
и общего решений, частного и общего
интегралов. Частным решением системы
(1) называется решение
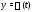 какой-нибудь ее задачи Коши (2) (именно:
задачи Коши с начальным условием
какой-нибудь ее задачи Коши (2) (именно:
задачи Коши с начальным условием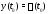 ).
).
Определение 2.Вектор-функция
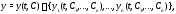
зависящая от
 произвольных постоянных
произвольных постоянных называется общим решениемсистемы
(1), если она удовлетворяет следующим
требованиям:
называется общим решениемсистемы
(1), если она удовлетворяет следующим
требованиям:
1) при любых допустимых значениях
постоянных
 функция
функция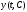 является решением системы (1) на
каком-нибудь отрезке
является решением системы (1) на
каком-нибудь отрезке ;
;
2) какова бы ни была начальная точка
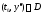 (
(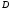 – область определения системы (1)),
существуют значения
– область определения системы (1)),
существуют значения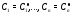 постоянных
постоянных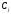 такие, что функция
такие, что функция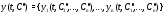 является решением задачи Коши (2) с
начальной точкой
является решением задачи Коши (2) с
начальной точкой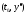 .
.
Условие 2) означает, что алгебраическая система уравнений

(относительно неизвестных
 )
имеет хотя бы одно решение. Заметим, что
в определении общего решения иногда
требуют, чтобы указанная алгебраическая
система уравнений имела единственное
решение
)
имеет хотя бы одно решение. Заметим, что
в определении общего решения иногда
требуют, чтобы указанная алгебраическая
система уравнений имела единственное
решение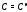 .
Это требование будет, очевидно, всегда
выполненным, если в области
.
Это требование будет, очевидно, всегда
выполненным, если в области реализуются все условия теоремы Коши.
реализуются все условия теоремы Коши.
Пример 1.Показать, что вектор-функция
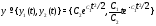
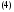
является общим решением системы
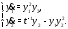
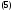
Решение.Вычислим производные от компонент вектор-функции (4):
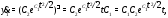
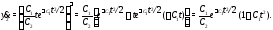
Вычислим правые части системы (5):
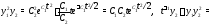

Сравнивая найденные значения производных
с вычисленными правыми частями, видим,
что при подстановке вектор-функции (4)
в систему (5) получаются тождества. Это
означает, что вектор-функция (4) является
решением системы (5) на любом отрезке
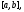 не содержащим точку
не содержащим точку
Рассмотрим теперь произвольную точку
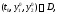 взятую из области
взятую из области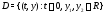 определения системы (5). Покажем, что
алгебраическая система уравнений (3)
имеет решение, В нашем случае (3) приобретает
вид
определения системы (5). Покажем, что
алгебраическая система уравнений (3)
имеет решение, В нашем случае (3) приобретает
вид
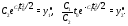
Умножая уравнения друг на друга, найдем, что
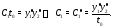
Подставляя это в первое уравнение, будем иметь

Таким образом, вектор-функция
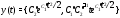 является решением системы (5) с начальным
условием
является решением системы (5) с начальным
условием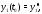
 Это означает, что вектор-функция (24.4)
является общим решением системы (5).
Это означает, что вектор-функция (24.4)
является общим решением системы (5).
Общий и частный интегралы системы
(1) определяются так же, как и в скалярном
случае: это есть общее и частное решения
системы (1), заданные соотношениями
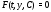 и
и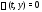 соответственно, из которых общее и
частное решения определяются как
функции, заданные неявно.
соответственно, из которых общее и
частное решения определяются как
функции, заданные неявно.
