Лекция 15. Построение фундаментальной матрицы решений дифференциальной системы с постоянной матрицей. Метод Эйлера.

Формула Коши (см. формулу (18) предыдущей лекции) позволяет вычислить общее реше-

ние системы если известна фундаментальная матрица решений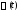соответствующей однородной системы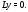Как и в случае скалярных уравнений, в которых роль фундаментальной матрицы играла фундаментальная система решений, построение матрицы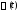представляет серьезные трудности и не всегда осуществимо. Однако если в системе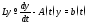матриц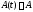апостоянна, то это можно всегда сделать. Но и в этом случае вычислительные трудности значительны, особенно если матрицаимеет кратные собственные значения. Поэтому здесь приводится алгоритм построения фундаментальной матрицы в случае простых корней характеристического уравнения. Напомним соответствующие понятия.

Пусть 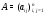– постоянная матрица порядка.

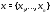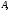Определение 1.Векторназывается собственным вектором матрицы соответствующим собственному значениюесли

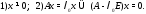
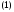
Здесь 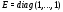– единичная матрица размерностиПоскольку в этом случае однородная алгебраическая система (1) имеет нетривиальное решение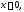тоОчевидно, верно и обратное: если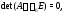то система (1) имеет нетривиальное решение

Определение 2.Уравнение

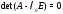
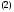
называется характеристическим уравнениемматрицы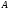(или характеристическим уравнением дифференциальной системы), а его корни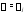– собственными значениямиэтой матрицы. При этом множествоназывается спектромматрицы.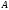

По каждому собственному значению можно вычислить соответствующий ему собственный вектор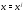(возможно, не единственный).

Определение 3.Спектр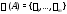матрицыназывается простым, если он состоит изразличных собственных значений (т.е.). В противном случае говорят, спектр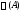матрицы 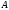кратный.

Нетрудно доказать следующие утверждения.

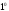) Двум различным собственным значениям иматрицысоответствуют два линейно независимых собственных вектора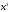и.

) Если спектр 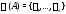матрицы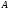простой, то совокупность всех собственных векторовэтой матрицы образует базис в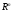(или в пространстве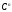–мерных комплексных векторов).

Если 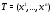– матрица из собственных векторов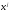матрицы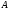, то имеет место равенство

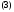
(в этом случае говорят, что матрица 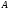подобнадиагональной матрице, а матрицу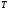называют преобразующей матрицей).

Рассмотрим теперь линейную однородную систему дифференциальных уравнений

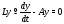
с постоянной матрицей 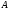. Связь спектра матрицы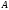с решениями этой системы устанавливается следующей теоремой.

Теорема Эйлера. Для того чтобы ненулевая вектор-функция была решением системы (4), необходимо и достаточно, чтобы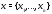был собственным вектором матрицы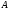, соответствующим собственному значению.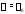

Доказательство.Подставим вектор-функцию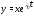в (4). Будем иметь

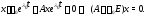
Отсюда видно, что если 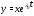является решением системы (4), то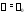– собственное значение матрицы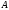, а– собственный вектор этой матрицы, соответствующий собственному значению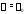. Очевидно, верно и обратное: если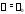и– соответствующие друг другу собственное значение и собственный вектор матрицы, то выполняются равенства

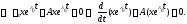
Последнее тождество означает, что вектор-функция 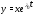– решение системы (4). Теорема доказана.

Воспользовавшись теоремой Эйлера, нетрудно построить фундаментальную матрицу решений системы (4) в случае простых корней характеристического уравнения (2).

Теорема 1. Если спектр 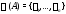постоянной матрицы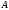простой, то матрица

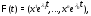
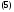
где 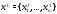– собственный вектор матрицы, соответствующий собственному значению, является фундаментальной матрицей решений системы (4) (на всей оси.

Доказательство.По теореме Эйлера каждый столбец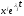матрицы (5) является решением системы (4). Покажем теперь, что матрица (5) не вырождена. Для этого достаточно проверить ее невырожденность в точке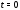. Имеем

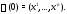
Поскольку все столбцы этой матрицы являются собственными векторами матрицы 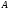, отвечающими различным собственным значениям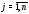, то они линейно независимы, и значитСледовательно, (5) является фундаментальной матрицей решений системы (4). Теорема доказана.

Следствие 1.В случае простого спектра 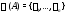матрицыобщее решение однородной системы (4) имеет вид

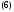
где – собственный вектор матрицы, соответствующий собственному значению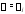,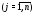;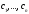– произвольные постоянные.

Заметим, что фундаментальную матрицу системы (4) можно построить и в случае кратных корней характеристического уравнения (2). Однако для этого нужно привлекать информацию о собственных и присоединенных векторах матрицы. Такая информация дается не во всех технических вузах, поэтому алгоритм построения фундаментальной матрицы решений в случае кратного спектра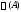здесь не излагается.

Пример 1.Решить систему уравнений

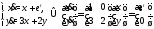
Решение.Матрица этой системы имеет вид

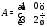
Ее собственные значения находим из характеристического уравнения

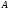Таким образом, спектр матрицыпростой. Вычисляем собственные вектора этой матрицы. Присистема (1) принимает вид

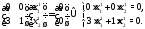
Поскольку первое уравнение этой системы удовлетворяется при любых и, то система (7) эквивалентна одному уравнению, и поэтому общее решение системы (7) имеет вид

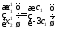
где 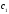– произвольная постоянная. Нас интересует вполне определенный собственный вектор, поэтому здесь можно положить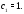Получим собственный вектор

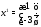
соответствующий собственному значению Для вычисления второго собственного вектора, соответствующего собственному значениюнадо решить систему

Она имеет общее решение вида

Положив здесь , получим собственный вектор

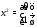
соответствующий собственному значению 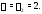По теореме 1 фундаментальная матрица решений однородной дифференциальной системы имеет вид

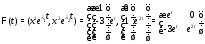
Для вычисления общего решения исходной неоднородной системы воспользуемся формулой Коши:

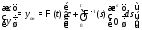
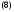
Вычислим матрицу

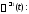
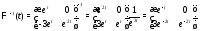
Теперь (8) принимает вид

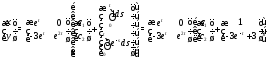
Это и есть решение исходной дифференциальной системы уравнений.

1 Здесь отрезок может быть заменён на промежутки причем могут быть равными

2 Функции и называют ещё коэффициентами уравнения (5).

3 Комплексная экспонента вводится ниже.

4См. учебное пособие “Острая О.В. Теория функций комплексного переменного.– Оренбург, 2008”.'

5 Точнее: точная нижняя грань множества таких чисел.

i

179