
- •3 Семестр (часть 1). Дифференциальные уравнения
- •1. Общие понятия
- •3. Дифференциальные уравнения с разделяющимися переменными. Однородные уравнения
- •1. Линейные дифференциальные уравнения. Метод вариации произвольной постоянной
- •2. Задача Коши. Теорема существования и единственности решения задачи Коши. Общее решение и общий интеграл
- •3. Уравнения, допускающие понижение порядка
- •1. Свойства дифференциального оператора. Теорема Коши
- •2. Линейная зависимость и линейная независимость системы функций. Вронскиан. Исследование линейной независимости с помощью вронскиана
- •3. Структура общего решения однородного дифференциального уравнения
- •Лекция 4. Общее решение неоднородного уравнения. Метод вариации произвольных постоянных Лагранжа. Комплексные решения дифференциальных уравнений. Построение фундаментальной системы решений
- •1. Структура общего решения неоднородного уравнения. Метод вариации произвольных постоянных Лагранжа
- •2.Метод вариации произвольных постоянных Лагранжа
- •3. Комплексные решения дифференциальных уравнений. Линейная независимость комплексных решений
- •Лекция 5. Линейные дифференциальные уравнения с постоянными коэффициентами. Метод Эйлера и метод подбора вычисления частных решений неоднородных уравнений
- •1. Метод Эйлера построения общего решения однородного дифференциального уравнения с постоянными коэффициентами в случае простых корней характеристического уравнения
- •2. Построение общего решения однородного дифференциального уравнения в случае кратных корней характеристического уравнения
- •3. Построение общего решения неоднородного уравнения с постоянными коэффициентами. Метод подбора частного решения неоднородного уравнения
- •Лекция 6. Комплексные числа и действия над ними. Функции комплексного переменного. Предел и непрерывность. Элементарные функции комплексного переменного и действия над ними
- •1. Извлечение корня й степени из комплексного числа. Множества в комплексной плоскости
- •2. Предел и непрерывность функции комплексной переменной
- •Лекция 7. Производная функции комплексного переменного. Аналитичность функции в точке и в области. Условия Коши-Римана. Элементарные аналитические функции
- •2. Геометрический смысл модуля и аргумента производной
- •Лекция 8 . Интеграл от функции комплексного переменного. Теорема Коши и для односвязной и многосвязной областей. Интегральная формула Коши. Существование всех производных для аналитической функции
- •2.2. Теорема Коши для односвязной области и многосвязной области. Интегральная формула Коши
- •3. Первообразная функции комплексных переменных
- •Лекция 9. Ряды в комплексной области. Степенные ряды. Теорема Абеля. Ряды Тейлора и Лорана
- •1. Степенные ряды. Ряды Тейлора и Лорана
- •Лекция 10. Изолированные особые точки. Ряды Лорана для функций, аналитических в кольце
- •1. Разложение функции в ряд Лорана
- •2. Нули аналитической функции и их связь с полюсами
- •3. Вычеты. Теорема Коши о вычетах
- •Лекция 11. Вычисление вычетов и применение теории вычетов для вычисления контурных и несобственных интегралов
- •1. Вычисление вычетов
- •2. Вычисление интегралов
- •Лекция 12. Преобразование Лапласа и его свойства. Применение к дифференциальным уравнениям
- •Лекция 13. Системы дифференциальных уравнений. Общие понятия
- •1. Понятия общего и частного решений. Задача Коши и ее разрешимость
- •2. Методы интегрирования систем дифференциальных уравнений
- •Лекция 14. Системы линейных дифференциальных уравнений
- •1. Глобальная теорема разрешимости начальной задачи для линейной системы дифференциальных уравнений
- •2. Линейная зависимость и линейная независимость системы произвольных вектор-функций и решений однородной системы уравнений
- •3. Фундаментальная матрица решений и структура общего решения однородной системы
- •4. Структура общего решения неоднородной системы дифференциальных уравнений
- •Лекция 15. Построение фундаментальной матрицы решений дифференциальной системы с постоянной матрицей. Метод Эйлера.
Лекция 5. Линейные дифференциальные уравнения с постоянными коэффициентами. Метод Эйлера и метод подбора вычисления частных решений неоднородных уравнений
На предыдушей
лекции были приведены примеры линейно
независимых систем функций. Сделано
это было не случайно, так как именно
такие функции образуют фундаментальные
системы решений дифференциальных
уравнений с постоянными коэффициентами.
Уравнения такого типа могут быть изучены
полностью, если будут найдены корни
соответствующих характеристических
многочленов (см. ни же
 ).
Построению корней этих многочленов (их
называют характеристическими числами)
и связи характеристических чисел с
решениями дифференциальных уравнений
уделяется основное внимание в настоящей
лекции.
).
Построению корней этих многочленов (их
называют характеристическими числами)
и связи характеристических чисел с
решениями дифференциальных уравнений
уделяется основное внимание в настоящей
лекции.
1. Метод Эйлера построения общего решения однородного дифференциального уравнения с постоянными коэффициентами в случае простых корней характеристического уравнения
Рассмотрим уравнение


с постоянными
коэффициентами
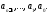 Построим по нему алгебраическое уравнение
Построим по нему алгебраическое уравнение


заменив в (1) производные
 на степени
на степени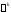 (
( ).
).
Определение
1. Многочлен
 называется
характерис-
называется
характерис-
тическим многочленом
уравнения (1), а само уравнение
 – характеристическим
уравнением,
соответствующим уравнению (1).
– характеристическим
уравнением,
соответствующим уравнению (1).
Имеет место очевидное тождество


если
 – постоянная, так как
– постоянная, так как
Теорема Эйлера.
Для того чтобы
экспонента
 (
( – постоянная) была решением уравнения
(1), необходимо и достаточно, чтобы
– постоянная) была решением уравнения
(1), необходимо и достаточно, чтобы было корнем характеристического
многочлена
было корнем характеристического
многочлена (или, что то же самое, корнем
характеристического уравнения
(или, что то же самое, корнем
характеристического уравнения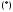 ).
).
Доказательство.
Действительно,
если
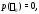 то из (2) следует тождество
то из (2) следует тождество показывающее, что экспонента
показывающее, что экспонента является решением уравнения (1). Обратно:
если
является решением уравнения (1). Обратно:
если – решение уравнения (1), то
– решение уравнения (1), то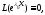 и из (2) следует, что
и из (2) следует, что т.е.
т.е. –
корень характеристического многочлена
–
корень характеристического многочлена Теорема доказана.
Теорема доказана.
Из теоремы Эйлера сразу же вытекает следующий результат.
Теорема 1.
Если все корни
 характеристического уравнения
характеристического уравнения различны (т.е.
различны (т.е.

 ),
то система функций
),
то система функций


образует фундаментальную систему решений уравнения (1). В этом случае общее решение (на любом отрезке [a,b]) уравнения (1) имеет вид


где
 –
произвольные постоянные.
–
произвольные постоянные.
Доказательство следует сразу из
теоремы Эйлера и утверждения
 предыдущей лекции.
предыдущей лекции.
Общее решение
(4) уравнения (1) может быть комплексным,
если хотя бы один из корней
 характеристического полинома
характеристического полинома комплексный. Для уравнений (1) с
действительными коэффициентами
комплексный. Для уравнений (1) с
действительными коэффициентами принято записывать общее решение в
действительной форме. Это нетрудно
сделать, если воспользоваться утверждением
принято записывать общее решение в
действительной форме. Это нетрудно
сделать, если воспользоваться утверждением лекции 4 и
отделив в комплексном решении
лекции 4 и
отделив в комплексном решении
 мнимую и действительную части:
мнимую и действительную части: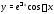 и
и Согласно
Согласно действительные функции
действительные функции и
и также являются решениями однородного
уравнения (1) с действительными
коэффициентами. Поступив так с каждой
комплексной экспонентой в
также являются решениями однородного
уравнения (1) с действительными
коэффициентами. Поступив так с каждой
комплексной экспонентой в ,
получим следующий результат.
,
получим следующий результат.
Теорема 2.
Пусть корни
 характеристического уравнения
характеристического уравнения различны, а коэффициенты
различны, а коэффициенты уравнения (1) действительны. Пусть, далее,
корни
уравнения (1) действительны. Пусть, далее,
корни –действительны, а остальные корни
–действительны, а остальные корни комплексны:
комплексны:

Тогда фундаментальную систему решений уравнения (1) можно выбрать в виде действительных функций


а общее решение уравнения (1) записать в виде

где
 –
произвольные постоянные.
–
произвольные постоянные.
Доказательство
следует из того, что функции (5) являются
решениями уравнения (1) (лекция 4,
утверждение
 )
и образуют линейно независимую систему
на любом отрезке
)
и образуют линейно независимую систему
на любом отрезке (лекция 4, утверждение
(лекция 4, утверждение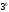 ).
Остаётся заметить, что в силу
действительности всех коэффициентов
).
Остаётся заметить, что в силу
действительности всех коэффициентов уравнения (1) его характеристическое
уравнение
уравнения (1) его характеристическое
уравнение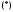 наряду с корнем
наряду с корнем имеет и комплексно-сопряженный корень
имеет и комплексно-сопряженный корень
Пример 1.Найти общее решение уравнения
Решение.
Составим характеристическое уравнение
 :
:

Разлагая его левую часть на множители, будем иметь

Итак, все корни характеристического уравнения различны. Согласно теореме 1 соответствующая фундаментальная система решений будет иметь вид

а значит общее решение исходного уравнения запишется в форме

