
- •3 Семестр (часть 1). Дифференциальные уравнения
- •1. Общие понятия
- •3. Дифференциальные уравнения с разделяющимися переменными. Однородные уравнения
- •1. Линейные дифференциальные уравнения. Метод вариации произвольной постоянной
- •2. Задача Коши. Теорема существования и единственности решения задачи Коши. Общее решение и общий интеграл
- •3. Уравнения, допускающие понижение порядка
- •1. Свойства дифференциального оператора. Теорема Коши
- •2. Линейная зависимость и линейная независимость системы функций. Вронскиан. Исследование линейной независимости с помощью вронскиана
- •3. Структура общего решения однородного дифференциального уравнения
- •Лекция 4. Общее решение неоднородного уравнения. Метод вариации произвольных постоянных Лагранжа. Комплексные решения дифференциальных уравнений. Построение фундаментальной системы решений
- •1. Структура общего решения неоднородного уравнения. Метод вариации произвольных постоянных Лагранжа
- •2.Метод вариации произвольных постоянных Лагранжа
- •3. Комплексные решения дифференциальных уравнений. Линейная независимость комплексных решений
- •Лекция 5. Линейные дифференциальные уравнения с постоянными коэффициентами. Метод Эйлера и метод подбора вычисления частных решений неоднородных уравнений
- •1. Метод Эйлера построения общего решения однородного дифференциального уравнения с постоянными коэффициентами в случае простых корней характеристического уравнения
- •2. Построение общего решения однородного дифференциального уравнения в случае кратных корней характеристического уравнения
- •3. Построение общего решения неоднородного уравнения с постоянными коэффициентами. Метод подбора частного решения неоднородного уравнения
- •Лекция 6. Комплексные числа и действия над ними. Функции комплексного переменного. Предел и непрерывность. Элементарные функции комплексного переменного и действия над ними
- •1. Извлечение корня й степени из комплексного числа. Множества в комплексной плоскости
- •2. Предел и непрерывность функции комплексной переменной
- •Лекция 7. Производная функции комплексного переменного. Аналитичность функции в точке и в области. Условия Коши-Римана. Элементарные аналитические функции
- •2. Геометрический смысл модуля и аргумента производной
- •Лекция 8 . Интеграл от функции комплексного переменного. Теорема Коши и для односвязной и многосвязной областей. Интегральная формула Коши. Существование всех производных для аналитической функции
- •2.2. Теорема Коши для односвязной области и многосвязной области. Интегральная формула Коши
- •3. Первообразная функции комплексных переменных
- •Лекция 9. Ряды в комплексной области. Степенные ряды. Теорема Абеля. Ряды Тейлора и Лорана
- •1. Степенные ряды. Ряды Тейлора и Лорана
- •Лекция 10. Изолированные особые точки. Ряды Лорана для функций, аналитических в кольце
- •1. Разложение функции в ряд Лорана
- •2. Нули аналитической функции и их связь с полюсами
- •3. Вычеты. Теорема Коши о вычетах
- •Лекция 11. Вычисление вычетов и применение теории вычетов для вычисления контурных и несобственных интегралов
- •1. Вычисление вычетов
- •2. Вычисление интегралов
- •Лекция 12. Преобразование Лапласа и его свойства. Применение к дифференциальным уравнениям
- •Лекция 13. Системы дифференциальных уравнений. Общие понятия
- •1. Понятия общего и частного решений. Задача Коши и ее разрешимость
- •2. Методы интегрирования систем дифференциальных уравнений
- •Лекция 14. Системы линейных дифференциальных уравнений
- •1. Глобальная теорема разрешимости начальной задачи для линейной системы дифференциальных уравнений
- •2. Линейная зависимость и линейная независимость системы произвольных вектор-функций и решений однородной системы уравнений
- •3. Фундаментальная матрица решений и структура общего решения однородной системы
- •4. Структура общего решения неоднородной системы дифференциальных уравнений
- •Лекция 15. Построение фундаментальной матрицы решений дифференциальной системы с постоянной матрицей. Метод Эйлера.
Лекция 10. Изолированные особые точки. Ряды Лорана для функций, аналитических в кольце
Сначала введём следующее понятие.
Определение 1.Ряд вида
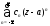
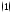
называется двухсторонним степенным рядом или рядом Лорана.
Ряд вида (1) сходится в области, в которой сходятся одновременно ряды
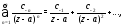

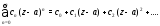
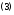
Ряд (2) сходится в области
 ,
т.е. вне замкнутого круга с центром в
точке
,
т.е. вне замкнутого круга с центром в
точке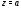 и радиуса
и радиуса ,
а ряд (3) – в круге
,
а ряд (3) – в круге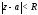 .
Поэтому: если 1)
.
Поэтому: если 1)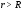 ,
то ряд (1) расходится всюду; 2) если
,
то ряд (1) расходится всюду; 2) если ,
то ряд (1) сходится в кольце
,
то ряд (1) сходится в кольце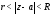 .
.
Пример 1. Определить область
сходимости ряда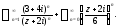
Решение.Для первого из рядов имеем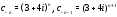 ,
Следовательно,
,
Следовательно,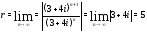 .
Значит, первый ряд сходится в области
.
Значит, первый ряд сходится в области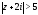 .
Для второго ряда имеем
.
Для второго ряда имеем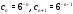 .
Радиус его сходимости
.
Радиус его сходимости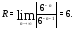 Значит,
второй ряд сходится в области
Значит,
второй ряд сходится в области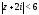 .
Таким образом, исходный двухсторонний
ряд ряд сходится в кольце
.
Таким образом, исходный двухсторонний
ряд ряд сходится в кольце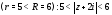 .
.
На предыдущей лекции была доказана
теорема 2, из которой следует, что если
функция
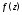 аналитична в
аналитична в то в окрестности любой точки
то в окрестности любой точки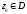 она не может быть представлена в виде
двухстороннего степенного ряда (1). Какие
же функции представляются такими рядами?
Ясно, что такие функции должны терять
аналитичность в точке
она не может быть представлена в виде
двухстороннего степенного ряда (1). Какие
же функции представляются такими рядами?
Ясно, что такие функции должны терять
аналитичность в точке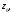 т.е.
эта точка должна быть особой для
т.е.
эта точка должна быть особой для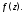 Дадим более точное понятие особой точки.
Дадим более точное понятие особой точки.
Определение 2. Говорят, что точка являетсяизолированной особой точкой
для функции
являетсяизолированной особой точкой
для функции
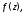 если сушествует проколотая окрестность
если сушествует проколотая окрестность этой точки такая, что функция
этой точки такая, что функция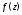 аналитична в
аналитична в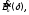 но
в самой точке
но
в самой точке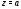 она либо не определена, либо на аналитична.
она либо не определена, либо на аналитична.
Определение 3. Изолированная особая
точка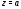 функции
функции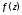 называетсяустранимой особой точкой,
если существует конечный предел
называетсяустранимой особой точкой,
если существует конечный предел Если
Если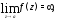 то точка
то точка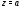 называетсяполюсом. Полюс
называетсяполюсом. Полюс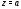 называетсяполюсом
называетсяполюсом
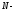 го
порядка, если существует конечный
предел
го
порядка, если существует конечный
предел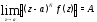 И, наконец, точка
И, наконец, точка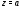 называетсясущественно особой точкой
для
называетсясущественно особой точкой
для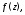 если не существует ни конечный, ни
бесконечный предел
если не существует ни конечный, ни
бесконечный предел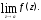
Нетрудно видеть, что если функция
 аналитична в точке
аналитична в точке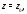 то она разлагается в степенной ряд
то она разлагается в степенной ряд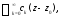 абсолютно сходящийся в круге с центром
в точке
абсолютно сходящийся в круге с центром
в точке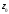 и с радиусом, равным расстоянию от
и с радиусом, равным расстоянию от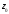 до ближайшей особой точки
до ближайшей особой точки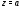 функции
функции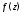 .
.
1. Разложение функции в ряд Лорана
Следующее утверждение устанавливает условия разложимости функции в двусторонние степенные ряды.
Теорема Лорана. Если функция
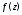 аналитична в кольце
аналитична в кольце
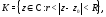
то в любой точке
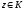 этого кольца она разлагается в
двухсторонний степенной ряд
этого кольца она разлагается в
двухсторонний степенной ряд
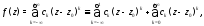

абсолютно сходящийся к
 При этом коэффициенты ряда (4) вычисляются
по формулам
При этом коэффициенты ряда (4) вычисляются
по формулам
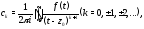
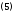
где
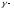 любой кусочно-гладкий замкнутый контур,
лежащий в кольце
любой кусочно-гладкий замкнутый контур,
лежащий в кольце ,
охватывающий точку
,
охватывающий точку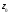 и обходимый против часовой стрелки.
и обходимый против часовой стрелки.
Доказательства этого утверждения основано на применении интегральной формулы Коши и проводится по аналогии с доказательством теоремы Тейлора.
Заметим, что ряд (4) называется рядом
Лорана для функции
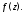 При этом его часть
При этом его часть
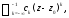 состоящая из отрицательных степеней
двучлена
состоящая из отрицательных степеней
двучлена называетсяглавной частью,а часть
называетсяглавной частью,а часть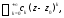 состоящая из неотрицательных степеней
двучлена
состоящая из неотрицательных степеней
двучлена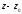 –правильной частьюряда Лорана (4) .
Чуть позже будет установлена связь типа
изолированной особой точки функции
–правильной частьюряда Лорана (4) .
Чуть позже будет установлена связь типа
изолированной особой точки функции c разложением в окрестности этой точки
в ряд Лорана функции
c разложением в окрестности этой точки
в ряд Лорана функции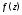 .
.
Рассмотрим примеры4.
Пример 2. Разложить функцию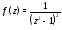 в ряд Лорана в кольце
в ряд Лорана в кольце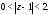
Решение. Надо представить функцию
в виде ряда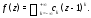 Преобразуем данную функцию:
Преобразуем данную функцию:
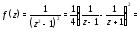
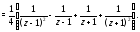

Первые два слагаемых в правой части (6)
имеют нужный вид, так как представляют
собой степени разности
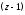 .
Последние два слагаемых запишем в виде:
.
Последние два слагаемых запишем в виде:
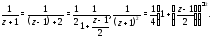
Применив формулу 1 таблицы 1, будем иметь
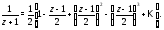
Дифференцированием по
 находим, что
находим, что

Подставляя найденные разложения в
формулу (6), получаем представление
функции
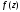 в кольце
в кольце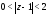 в виде ряда Лорана:
в виде ряда Лорана:
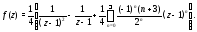
Пример 3. Разложить в ряд Лорана
функцию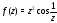 в окрестности точки
в окрестности точки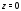 .
.
Решение. Используем разложение
(см. таблицу 1)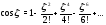 .
Полагая здесь
.
Полагая здесь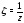 ,
будем иметь
,
будем иметь
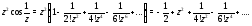
Это
разложение справедливо для любой точки
 .
В данном случае кольцо представляет
собой всю комплексную плоскость с одной
выброшенной точкой
.
В данном случае кольцо представляет
собой всю комплексную плоскость с одной
выброшенной точкой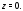
Пример 4. Разложить функцию
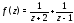
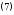
по степеням
 в ряды Лорана с учетом ее особых точек.
в ряды Лорана с учетом ее особых точек.
Решение. Функция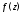 имеет две особые точки:
имеет две особые точки: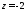 и
и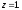
а) Разложение в круге
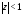 .
Преобразуем (7) следующим образом:
.
Преобразуем (7) следующим образом:
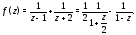

Используя формулу 1 из таблицы 1, получаем, что
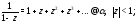

Подставляя эти разложения в (8), будем иметь
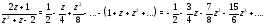
Это есть разложение в ряд Тейлора функции
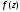 .
.
б) Разложение в кольце
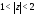 .
Ряд
.
Ряд для функции
для функции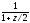 остается сходящимся в этом кольце, так
как
остается сходящимся в этом кольце, так
как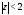 .
Ряд
.
Ряд для функции
для функции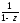 расходится для
расходится для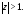 Поэтому преобразуем
Поэтому преобразуем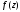 следующим образом:
следующим образом:
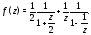
Применяя формулу 1 таблицы 1, будем иметь

Этот ряд сходится, если
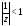 ,
т.е. при
,
т.е. при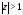 .
Подставляя это разложение и разложение
.
Подставляя это разложение и разложение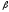 в (9), найдем, что
в (9), найдем, что
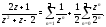
в) Разложение для
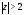 .
Функцию
.
Функцию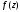 представим в виде
представим в виде
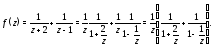
Тогда
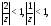 так как
так как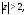 поэтому можно применить формулу 1 таблицы
1 и получить, что
поэтому можно применить формулу 1 таблицы
1 и получить, что
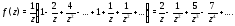
Пример 5. Разложить в ряд Лорана
функцию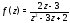 в окрестности ее особых точек.
в окрестности ее особых точек.
Решение.Особые точки функции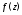 :
: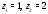 .
.
а) Чтобы записать разложение функции
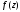 в окрестности точки
в окрестности точки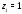 ,
т.е. в кольце
,
т.е. в кольце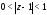 ,
представим функцию
,
представим функцию в виде суммы простейших дробей:
в виде суммы простейших дробей:
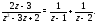

Правую часть (10) преобразуем следующим образом:
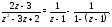
Применяя формулу 1 таблицы 1 (в которой
 заменим на
заменим на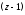 ),
получим
),
получим
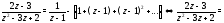
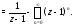
б) Разложение функции
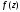 в окрестности точки
в окрестности точки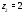 ,
т.е. в кольце
,
т.е. в кольце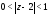 ,
получим следующим образом:
,
получим следующим образом:
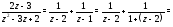
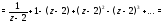

Установим теперь связь типа особой
точки
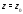 функции
функции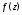 с разложением этой функции в ряд Лорана
в окрестности точки
с разложением этой функции в ряд Лорана
в окрестности точки .
.
Теорема 1.а) Точка
 является устранимой особой точкой
функции
является устранимой особой точкой
функции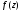 тогда и только тогда, когда разложение
этой функции в ряд Лорана в окрестности
точки
тогда и только тогда, когда разложение
этой функции в ряд Лорана в окрестности
точки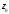 не содержит главной части.
не содержит главной части.
б) Точка
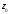 является полюсом порядка
является полюсом порядка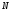 функции
функции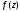 тогда и только тогда, когда в разложении
функции
тогда и только тогда, когда в разложении
функции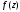 в ряд Лорана в окрестности точки
в ряд Лорана в окрестности точки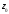 главная часть разложения содержит
конечное число членов, причем младшим
отличным от нуля коэффициентом является
главная часть разложения содержит
конечное число членов, причем младшим
отличным от нуля коэффициентом является .
.
в) Точка
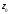 является существенно особой точкой
функции
является существенно особой точкой
функции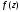 тогда и только тогда, когда главная
часть разложения функции в ряд Лорана
в окрестности точки
тогда и только тогда, когда главная
часть разложения функции в ряд Лорана
в окрестности точки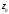 содержит бесконечное число членов.
содержит бесконечное число членов.
Доказательствопроведем для
утверждений а) и б). Разложим функцию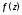 в ряд Лорана в окрестности точки
в ряд Лорана в окрестности точки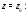
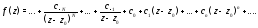

Устремляя здесь
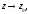 видим, что конечный предел
видим, что конечный предел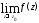 существует тогда и только тогда, когда
все
существует тогда и только тогда, когда
все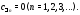 При этом
При этом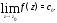 Значит, точка
Значит, точка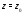 будет устранимой особой точкой функции
будет устранимой особой точкой функции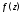 тогда и только тогда, когда ряд Лорана
(11) не содержит главной части. Утверждение
а) доказано.
тогда и только тогда, когда ряд Лорана
(11) не содержит главной части. Утверждение
а) доказано.
Умножим теперь обе части равенства (11)
на
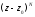 .
Получим разложение
.
Получим разложение
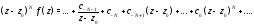
Отсюда видно, что конечный предел
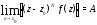 существует тогда и только тогда, когда
существует тогда и только тогда, когда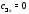 для
всех
для
всех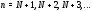 . Это означает, что точка
. Это означает, что точка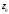 является полюсом порядка
является полюсом порядка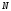 функции
функции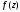 тогда и только тогда, когда в разложении
функции
тогда и только тогда, когда в разложении
функции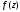 в ряд Лорана в окрестности точки
в ряд Лорана в окрестности точки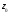 главная часть разложения содержит
конечное число членов, причем младшим
отличным от нуля коэффициентом является
главная часть разложения содержит
конечное число членов, причем младшим
отличным от нуля коэффициентом является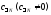 ,
т.е. верно утверждение б). Теорема
доказана.
,
т.е. верно утверждение б). Теорема
доказана.
