
- •3 Семестр (часть 1). Дифференциальные уравнения
- •1. Общие понятия
- •3. Дифференциальные уравнения с разделяющимися переменными. Однородные уравнения
- •1. Линейные дифференциальные уравнения. Метод вариации произвольной постоянной
- •2. Задача Коши. Теорема существования и единственности решения задачи Коши. Общее решение и общий интеграл
- •3. Уравнения, допускающие понижение порядка
- •1. Свойства дифференциального оператора. Теорема Коши
- •2. Линейная зависимость и линейная независимость системы функций. Вронскиан. Исследование линейной независимости с помощью вронскиана
- •3. Структура общего решения однородного дифференциального уравнения
- •Лекция 4. Общее решение неоднородного уравнения. Метод вариации произвольных постоянных Лагранжа. Комплексные решения дифференциальных уравнений. Построение фундаментальной системы решений
- •1. Структура общего решения неоднородного уравнения. Метод вариации произвольных постоянных Лагранжа
- •2.Метод вариации произвольных постоянных Лагранжа
- •3. Комплексные решения дифференциальных уравнений. Линейная независимость комплексных решений
- •Лекция 5. Линейные дифференциальные уравнения с постоянными коэффициентами. Метод Эйлера и метод подбора вычисления частных решений неоднородных уравнений
- •1. Метод Эйлера построения общего решения однородного дифференциального уравнения с постоянными коэффициентами в случае простых корней характеристического уравнения
- •2. Построение общего решения однородного дифференциального уравнения в случае кратных корней характеристического уравнения
- •3. Построение общего решения неоднородного уравнения с постоянными коэффициентами. Метод подбора частного решения неоднородного уравнения
- •Лекция 6. Комплексные числа и действия над ними. Функции комплексного переменного. Предел и непрерывность. Элементарные функции комплексного переменного и действия над ними
- •1. Извлечение корня й степени из комплексного числа. Множества в комплексной плоскости
- •2. Предел и непрерывность функции комплексной переменной
- •Лекция 7. Производная функции комплексного переменного. Аналитичность функции в точке и в области. Условия Коши-Римана. Элементарные аналитические функции
- •2. Геометрический смысл модуля и аргумента производной
- •Лекция 8 . Интеграл от функции комплексного переменного. Теорема Коши и для односвязной и многосвязной областей. Интегральная формула Коши. Существование всех производных для аналитической функции
- •2.2. Теорема Коши для односвязной области и многосвязной области. Интегральная формула Коши
- •3. Первообразная функции комплексных переменных
- •Лекция 9. Ряды в комплексной области. Степенные ряды. Теорема Абеля. Ряды Тейлора и Лорана
- •1. Степенные ряды. Ряды Тейлора и Лорана
- •Лекция 10. Изолированные особые точки. Ряды Лорана для функций, аналитических в кольце
- •1. Разложение функции в ряд Лорана
- •2. Нули аналитической функции и их связь с полюсами
- •3. Вычеты. Теорема Коши о вычетах
- •Лекция 11. Вычисление вычетов и применение теории вычетов для вычисления контурных и несобственных интегралов
- •1. Вычисление вычетов
- •2. Вычисление интегралов
- •Лекция 12. Преобразование Лапласа и его свойства. Применение к дифференциальным уравнениям
- •Лекция 13. Системы дифференциальных уравнений. Общие понятия
- •1. Понятия общего и частного решений. Задача Коши и ее разрешимость
- •2. Методы интегрирования систем дифференциальных уравнений
- •Лекция 14. Системы линейных дифференциальных уравнений
- •1. Глобальная теорема разрешимости начальной задачи для линейной системы дифференциальных уравнений
- •2. Линейная зависимость и линейная независимость системы произвольных вектор-функций и решений однородной системы уравнений
- •3. Фундаментальная матрица решений и структура общего решения однородной системы
- •4. Структура общего решения неоднородной системы дифференциальных уравнений
- •Лекция 15. Построение фундаментальной матрицы решений дифференциальной системы с постоянной матрицей. Метод Эйлера.
1. Свойства дифференциального оператора. Теорема Коши
Мы предполагаем, что читатель знаком с понятием линейного пространства и с основными его свойствами. В дальнейшем будут использоваться следующие пространства:
1)
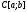 – пространство функций, непрерывных
на отрезке
– пространство функций, непрерывных
на отрезке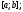
2)
 – пространство функций
– пространство функций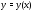 непрерывных вместе со своими производными
непрерывных вместе со своими производными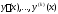 (до
(до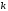 –го
порядка включительно),
–го
порядка включительно),
Эти пространства являются линейными пространствами с обычными для функций операциями сложения и умножения на числа.
Теорема 1.
Если в операторе
 все коэффициенты
все коэффициенты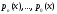 непрерывны на отрезке
непрерывны на отрезке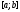 ,
то
,
то действует из пространства
действует из пространства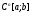 в пространство
в пространство (т.е.
(т.е.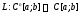 )
и является линейным оператором, т.е.
)
и является линейным оператором, т.е.

для произвольных
постоянных
 и
и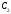 и произвольных функций
и произвольных функций
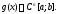
Действительно,
при дифференцировании теряется гладкость
функции на единицу, значит при
 –кратном
дифференцировании функция класса
–кратном
дифференцировании функция класса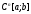 переходит в функцию класса
переходит в функцию класса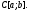 Кроме того, поскольку операция
дифференцирования линейна, то и линеен
оператор
Кроме того, поскольку операция
дифференцирования линейна, то и линеен
оператор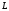 Будем рассматривать в основном уравнения
(1) со старшим коэффициентом
Будем рассматривать в основном уравнения
(1) со старшим коэффициентом B этом случае на него можно поделить
уравнение (1) и записать его в форме
B этом случае на него можно поделить
уравнение (1) и записать его в форме
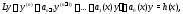
где обозначено:

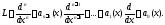
Наша ближайшая задача – изучить свойства решений этого уравнения. Начнем с теоремы существования и единственности решения задачи Коши

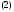
где
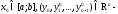 произвольный вектор.
произвольный вектор.
Теорема 2 (Коши)
.
Если в уравнении (2) все коэффициенты
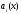 и правая часть
и правая часть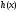 непрерывны на отрезке
непрерывны на отрезке ,
то задача Коши (2) для этого уравнения
имеет единственное решение
,
то задача Коши (2) для этого уравнения
имеет единственное решение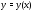 и это решение определено также на этом
отрезке.
и это решение определено также на этом
отрезке.
Таким образом, теорема существования и единственности решения начальной задачи для линейного дифференциального уравнения носит "глобальный" характер в отличие от "локального" характера общей теоремы существования единственности решения для нелинейного уравнения.
2. Линейная зависимость и линейная независимость системы функций. Вронскиан. Исследование линейной независимости с помощью вронскиана
Пусть функции
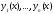 имеют смысл на отрезке
имеют смысл на отрезке
Определение 1.
Говорят, что
система функций
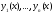 линейно
зависима на
отрезке
линейно
зависима на
отрезке
 ,
если существуют постоянные
,
если существуют постоянные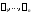 ,
не равные нулю одновременно, такие, что
имеет место тождество
,
не равные нулю одновременно, такие, что
имеет место тождество
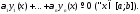

Если же тождество
(3), где
 – постоянные, выполняется тогда и только
тогда, когда все числа
– постоянные, выполняется тогда и только
тогда, когда все числа равны нулю (
равны нулю ( то система функций
то система функций называется
линейно независимой
на отрезке
называется
линейно независимой
на отрезке
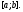
Аналогично
определяется
линейная зависимость
и линейная
независимость
на промежутках
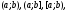 причем не исключается и случай бесконечного
промежутка. Заметим, что выражение
причем не исключается и случай бесконечного
промежутка. Заметим, что выражение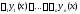 называется линейной комбинацией функций
называется линейной комбинацией функций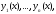 а числа
а числа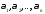 – коэффициентами линейной комбинации.
– коэффициентами линейной комбинации.
Пример 1. Доказать, что система функций
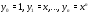
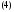
линейно независима
на любом отрезке
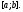
Решение.Составим линейную комбинацию функций (4) и посмотрим, когда она тождественно обращается в нуль:
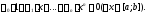
Слева стоит многочлен
с коэффициентами
 Само тождество означает, что любое число
Само тождество означает, что любое число из отрезка
из отрезка является корнем этого многочлена. Если
хотя бы один из коэффициентов
является корнем этого многочлена. Если
хотя бы один из коэффициентов не равен нулю, то получилось бы, что
указанный многочлен имеет бесчисленное
число корней, что невозможно. Значит,
все числа
не равен нулю, то получилось бы, что
указанный многочлен имеет бесчисленное
число корней, что невозможно. Значит,
все числа равны нулю, поэтому функции (4) линейно
независимы на отрезке
равны нулю, поэтому функции (4) линейно
независимы на отрезке
Пример 2.
Будут ли линейно зависимыми на промежутке
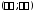 функции
функции
 ?
?
Решение.Линейная
комбинация
 тождественно обращается в нуль на
промежутке
тождественно обращается в нуль на
промежутке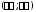 ,
если взять числа
,
если взять числа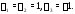 Так как они не равны нулю (достаточно
было бы, чтобы хотя бы одно из них не
равнялось нулю), то указанные функции
линейно зависимы на промежутке
Так как они не равны нулю (достаточно
было бы, чтобы хотя бы одно из них не
равнялось нулю), то указанные функции
линейно зависимы на промежутке Ответ: да.
Ответ: да.
Теорема 3.
Если система
функций
 линейно завиcима на отрезке
линейно завиcима на отрезке то хотя бы одна из них является линейной
комбинацией других (на этом отрезке).
Обратно: если одна из функций
то хотя бы одна из них является линейной
комбинацией других (на этом отрезке).
Обратно: если одна из функций является на отрезке
является на отрезке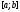 линейной комбинацией других, то система
линейной комбинацией других, то система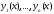 линейно зависима на отрезке
линейно зависима на отрезке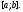
Доказательство.
Пусть функции
 линейно зависимы на отрезке
линейно зависимы на отрезке Тогда найдутся числа
Тогда найдутся числа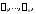 не равные нулю одновременно, такие, что
не равные нулю одновременно, такие, что

Пусть,
например,
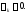 Тогда можно записать
Тогда можно записать

т.е. функция
 является линейной комбинацией функций
является линейной комбинацией функций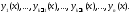 Обратно: если выполняется тождество
Обратно: если выполняется тождество
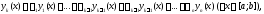
то
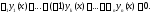 Мы видим, что тождество (3) имеет место
при числах
Мы видим, что тождество (3) имеет место
при числах не равных нулю одновременно. Следовательно,
система функций
не равных нулю одновременно. Следовательно,
система функций линейно зависима. Теорема доказана.
линейно зависима. Теорема доказана.
Очевидны следующие утверждения.
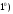 Если система функций
Если система функций
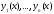 содержит функцию
содержит функцию то она линейно зависима (на отрезке
то она линейно зависима (на отрезке ,
на котором указанные функции имеют
смысл).
,
на котором указанные функции имеют
смысл).
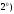 Если какая-нибудь
подсистема системы функций
Если какая-нибудь
подсистема системы функций
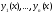 линейно зависима, то и вся система
линейно зависима, то и вся система линейно зависима.
линейно зависима.
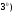 Если система функций
Если система функций
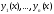 линейно зависима на отрезке
линейно зависима на отрезке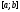 ,
то она линейно зависима и на любом
отрезке
,
то она линейно зависима и на любом
отрезке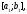 лежащем внутри отрезка
лежащем внутри отрезка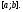
 Если система функций
Если система функций
 линейно независима на отрезке
линейно независима на отрезке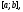 то она линейно независима и на любом
отрезке
то она линейно независима и на любом
отрезке ,
содержащем отрезок
,
содержащем отрезок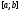 (если, конечно, функции
(если, конечно, функции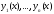 определены на отрезке
определены на отрезке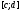 ).
).
Заметим, что свойство линейной зависимости функций нельзя продолжить на больший отрезок, а свойство линейной независимости – сузить на меньший отрезок.Дадим эффективный способ проверки линейной зависимости или линейной независимости системы функций с помощью определителя Вронского.
Определение
2.
Определителем Вронского
(или просто вронскианом) системы функций
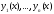 ,
принадлежащих пространству
,
принадлежащих пространству ,
называется определитель
,
называется определитель

первую строку
которого образуют данные функции
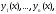 а последующие строки являются производными
функций предыдущей строки. Матрицу
этого определителя мы будем называть
матрицей Вронского.
а последующие строки являются производными
функций предыдущей строки. Матрицу
этого определителя мы будем называть
матрицей Вронского.
Теорема 4
(необходимое
условие линейной зависимости функций).
Если функции
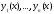 линейно зависимы на отрезке
линейно зависимы на отрезке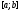 ,
то их вронскиан обращается тождественно
в нуль на этом отрезке, т.е.
,
то их вронскиан обращается тождественно
в нуль на этом отрезке, т.е.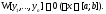
Доказательство.
Поскольку функции
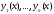 линейно зависимы на отрезке
линейно зависимы на отрезке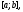 то существуют числа
то существуют числа не равные нулю одновременно, такие, что
имеет место тождество
не равные нулю одновременно, такие, что
имеет место тождество
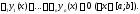
Дифференцируя это
тождество
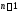 раз, получаем еще
раз, получаем еще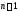 тождество. Вместе с предыдущим тождеством
они образуют однородную систему
алгебраических уравнений:
тождество. Вместе с предыдущим тождеством
они образуют однородную систему
алгебраических уравнений:
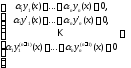

которая (в силу
линейной зависимости функций
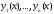 )
имеет при каждом
)
имеет при каждом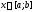 ненулевое решение
ненулевое решение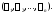 Но тогда определитель этой системы,
являющийся определителем Вронского
функций
Но тогда определитель этой системы,
являющийся определителем Вронского
функций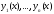 ,
обращается в нуль при каждом
,
обращается в нуль при каждом т.е.
т.е.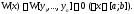 Теорема доказана.
Теорема доказана.
Заметим, что
обратное утверждение для произвольной
системы функций
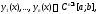 не имеет место.
не имеет место.
Пример 3. Показать, что функции
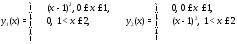
линейно независимы
на отрезке
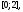 но
но
Решение.
Посмотрим,
при каких постоянных
 и
и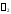 выполняется тождество
выполняется тождество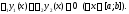 При
При имеем
имеем Это тождество имеет место при
Это тождество имеет место при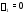 и при произвольном
и при произвольном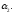 На промежутке
На промежутке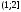 имеем
имеем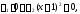 откуда выводим, что
откуда выводим, что Итак, тождество
Итак, тождество на всем промежутке
на всем промежутке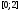 имеет место лишь при
имеет место лишь при Значит, функции
Значит, функции и
и линейно независимы на отрезке
линейно независимы на отрезке С другой стороны,
С другой стороны,

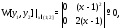
т.е. определитель
Вронского
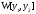 тождественно обращается в нуль на
отрезке
тождественно обращается в нуль на
отрезке

Ситуация, описанная
в этом примере, не реализуется, если
 и
и являются решениями однородного уравнения
являются решениями однородного уравнения с непрерывными на отрезке
с непрерывными на отрезке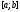 коэффициентами. Это будет показано
ниже. Теорему 4. применяют при установлении
линейной независимости функций.
коэффициентами. Это будет показано
ниже. Теорему 4. применяют при установлении
линейной независимости функций.
Следствие 1.
Если вронскиан системы функций
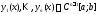 не равен нулю хотя бы в одной точке
не равен нулю хотя бы в одной точке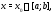 то указанные функции линейно независимы
на отрезке
то указанные функции линейно независимы
на отрезке
Действительно,
если бы
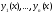 были линейно зависимы на отрезке
были линейно зависимы на отрезке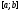 ,
то
,
то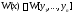 тождественно обращался бы в нуль на
этом отрезке, а значит, в частности, он
был бы равен нулю в точке
тождественно обращался бы в нуль на
этом отрезке, а значит, в частности, он
был бы равен нулю в точке чего быть не может.
чего быть не может.
