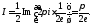- •3 Семестр (часть 1). Дифференциальные уравнения
- •1. Общие понятия
- •3. Дифференциальные уравнения с разделяющимися переменными. Однородные уравнения
- •1. Линейные дифференциальные уравнения. Метод вариации произвольной постоянной
- •2. Задача Коши. Теорема существования и единственности решения задачи Коши. Общее решение и общий интеграл
- •3. Уравнения, допускающие понижение порядка
- •1. Свойства дифференциального оператора. Теорема Коши
- •2. Линейная зависимость и линейная независимость системы функций. Вронскиан. Исследование линейной независимости с помощью вронскиана
- •3. Структура общего решения однородного дифференциального уравнения
- •Лекция 4. Общее решение неоднородного уравнения. Метод вариации произвольных постоянных Лагранжа. Комплексные решения дифференциальных уравнений. Построение фундаментальной системы решений
- •1. Структура общего решения неоднородного уравнения. Метод вариации произвольных постоянных Лагранжа
- •2.Метод вариации произвольных постоянных Лагранжа
- •3. Комплексные решения дифференциальных уравнений. Линейная независимость комплексных решений
- •Лекция 5. Линейные дифференциальные уравнения с постоянными коэффициентами. Метод Эйлера и метод подбора вычисления частных решений неоднородных уравнений
- •1. Метод Эйлера построения общего решения однородного дифференциального уравнения с постоянными коэффициентами в случае простых корней характеристического уравнения
- •2. Построение общего решения однородного дифференциального уравнения в случае кратных корней характеристического уравнения
- •3. Построение общего решения неоднородного уравнения с постоянными коэффициентами. Метод подбора частного решения неоднородного уравнения
- •Лекция 6. Комплексные числа и действия над ними. Функции комплексного переменного. Предел и непрерывность. Элементарные функции комплексного переменного и действия над ними
- •1. Извлечение корня й степени из комплексного числа. Множества в комплексной плоскости
- •2. Предел и непрерывность функции комплексной переменной
- •Лекция 7. Производная функции комплексного переменного. Аналитичность функции в точке и в области. Условия Коши-Римана. Элементарные аналитические функции
- •2. Геометрический смысл модуля и аргумента производной
- •Лекция 8 . Интеграл от функции комплексного переменного. Теорема Коши и для односвязной и многосвязной областей. Интегральная формула Коши. Существование всех производных для аналитической функции
- •2.2. Теорема Коши для односвязной области и многосвязной области. Интегральная формула Коши
- •3. Первообразная функции комплексных переменных
- •Лекция 9. Ряды в комплексной области. Степенные ряды. Теорема Абеля. Ряды Тейлора и Лорана
- •1. Степенные ряды. Ряды Тейлора и Лорана
- •Лекция 10. Изолированные особые точки. Ряды Лорана для функций, аналитических в кольце
- •1. Разложение функции в ряд Лорана
- •2. Нули аналитической функции и их связь с полюсами
- •3. Вычеты. Теорема Коши о вычетах
- •Лекция 11. Вычисление вычетов и применение теории вычетов для вычисления контурных и несобственных интегралов
- •1. Вычисление вычетов
- •2. Вычисление интегралов
- •Лекция 12. Преобразование Лапласа и его свойства. Применение к дифференциальным уравнениям
- •Лекция 13. Системы дифференциальных уравнений. Общие понятия
- •1. Понятия общего и частного решений. Задача Коши и ее разрешимость
- •2. Методы интегрирования систем дифференциальных уравнений
- •Лекция 14. Системы линейных дифференциальных уравнений
- •1. Глобальная теорема разрешимости начальной задачи для линейной системы дифференциальных уравнений
- •2. Линейная зависимость и линейная независимость системы произвольных вектор-функций и решений однородной системы уравнений
- •3. Фундаментальная матрица решений и структура общего решения однородной системы
- •4. Структура общего решения неоднородной системы дифференциальных уравнений
- •Лекция 15. Построение фундаментальной матрицы решений дифференциальной системы с постоянной матрицей. Метод Эйлера.
Лекция 11. Вычисление вычетов и применение теории вычетов для вычисления контурных и несобственных интегралов
Преходим к изложению теории вычетов и их применению к вычислению комплексных интегралов по замкнутому контуру и действительных несобственных интегралов.
1. Вычисление вычетов
Универсальный способ вычисления
вычета в изолированной особой точке
 – это вычисление по определению
– это вычисление по определению
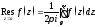
Однако
он не всегда приводит к цели, так как
связан с вычислением интеграла, которое
может оказаться весьма не простым.
Второй способ основан на разложении
функции в ряд Лорана и выделении в нем
коэффициента при
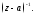 Тогда
Тогда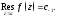 Но и этот способ часто приводит к
громоздким вычислениям. Поэтому дадим
сравнительно простой способ, основанный
на следующем утверждении.
Но и этот способ часто приводит к
громоздким вычислениям. Поэтому дадим
сравнительно простой способ, основанный
на следующем утверждении.
Теорема 1.Пусть
 изолированная особая точка функции
изолированная особая точка функции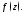 Тогда:
Тогда:
1. если
 – устранимая особая точка функции
– устранимая особая точка функции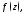 то
то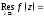 0;
0;
2. если
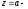 полюс первого порядка функции
полюс первого порядка функции то
он может вычислен двумя способами:
то
он может вычислен двумя способами:
а)
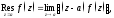
б)
(здесь
 аналитические
в точке
аналитические
в точке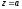 функции, причем
функции, причем );
);
3. если
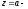 полюс
полюс го порядка функции
го порядка функции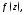 то
то
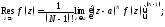

4) если
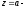 существенно
особая точка функции
существенно
особая точка функции то
вычет в ней вычисляют после разложения
то
вычет в ней вычисляют после разложения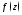 в ряд Лорана в окрестности точки
в ряд Лорана в окрестности точки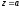 ;
тогда
;
тогда коэффициент
при
коэффициент
при в этом разложении.
в этом разложении.
Доказательство. Утверждение 1
очевидно, так как в разложении функции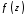 в ряд Лорана в окрестности устранимой
особой точке нет главной части, и значит,
в ряд Лорана в окрестности устранимой
особой точке нет главной части, и значит,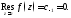 Утверждение 2а вытекает из утверждения
3. Докажем его.
Утверждение 2а вытекает из утверждения
3. Докажем его.
Запишем разложение функции
 в ряд Лорана:
в ряд Лорана:
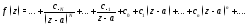
Умножая его обе части на
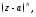 получим
получим

Чтобы
найти коэффициент
 продифференцируем последнее равенство
продифференцируем последнее равенство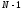 раз по
раз по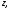 и перейдём в полученном равенстве к
пределу при
и перейдём в полученном равенстве к
пределу при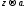 Получим
Получим

Формула (1) доказана. Утверждение 2б
вытекает из утверждения 2а, если в нем
заменить
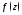 на
на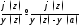 и перейти к пределу при
и перейти к пределу при Теорема доказана.
Теорема доказана.
2. Вычисление интегралов
1. Непосредственное применение
теоремы Коши о вычетах. Рассмотрим
интеграл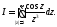 Вычислим вычет в единственной особой
точке
Вычислим вычет в единственной особой
точке подынтегральной функции
подынтегральной функции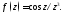 Так как
Так как является полюсом 3-го порядка функции
является полюсом 3-го порядка функции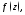 то вычет можно было бы подсчитать по
формуле (1). Однако удобнее это сделать,
разложив
то вычет можно было бы подсчитать по
формуле (1). Однако удобнее это сделать,
разложив в ряд Лорана в окрестности особой точки:
в ряд Лорана в окрестности особой точки:
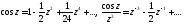
Следовательно,
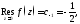 и по теореме Коши о вычетах получаем,
что
и по теореме Коши о вычетах получаем,
что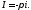
2.Интегралы вида
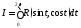 (
( дробно-рациональная
функция.Здесь надо сделать замену
дробно-рациональная
функция.Здесь надо сделать замену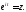 Тогда
Тогда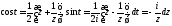 и интеграл преобразуется к виду
и интеграл преобразуется к виду где
где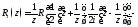
также дробно-рациональная функция.
Теперь надо применить теорему Коши о
вычетах и получить, что
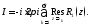
Пример 1.Вычислить интеграл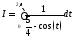 .
.
Решение. Имеем
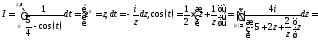
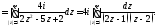
Подынтегральная функция
 имеет два простых полюса:
имеет два простых полюса: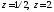 Внутрь контура
Внутрь контура попадает только одна точка
попадает только одна точка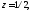 поэтому
поэтому

3. Вычисление несобственных интегралов. Прежде чем перейти к изложению этой темы, докажем сначала следующее вспомогательное утверждение.
Лемма 1. Пусть
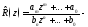 правильная дробь (т.е.
правильная дробь (т.е.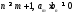 ).
Тогда для любой постоянной
).
Тогда для любой постоянной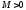 существует число
существует число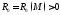 такое, что при всех
такое, что при всех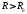 имеет место оценка
имеет место оценка
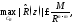
где
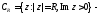 полуокружность радиуса
полуокружность радиуса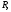 лежащая в верхней полуплоскости
лежащая в верхней полуплоскости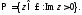
Доказательство. Имеем
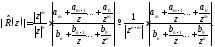
Так как существует конечный предел
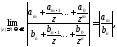 то
для любой фиксированной постоянной
то
для любой фиксированной постоянной найдётся
найдётся такое, что при всех
такое, что при всех выполняется неравенство
выполняется неравенство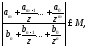 а значит,
а значит,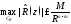 при
при
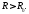 Лемма доказана.
Лемма доказана.
Теперь нетрудно обосновать следующее утверждение.
Теорема 2.
Пусть для
интеграла

выполнены условия:
1)
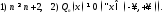
Тогда
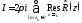
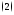
(здесь
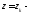 нули знаменателя
нули знаменателя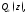 лежащие
в верхней полуплоскости
лежащие
в верхней полуплоскости
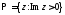 ).
).
Доказательство.
Проведём
полуокружность
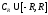 так, чтобы все особые точки (нули
знаменателя
так, чтобы все особые точки (нули
знаменателя ),
лежащие в верхней полуплоскости
),
лежащие в верхней полуплоскости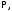 оказались
внутри неё. По теореме Коши о вычетах
имеем
оказались
внутри неё. По теореме Коши о вычетах
имеем

Правая часть этого
равенства не зависит от
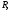 поэтому устремляя в нем
поэтому устремляя в нем и учитывая, что
и учитывая, что и что (см. лемму 1 и условие 2)
и что (см. лемму 1 и условие 2)
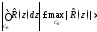 дл.
дл.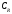
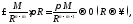
получаем утверждение теоремы.
При вычислении
интегралов вида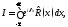 где
где правильная дробь, используется следующее
утверждение.
правильная дробь, используется следующее
утверждение.
Лемма Жордана. Пусть функция
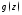 удовлетворяет требованиям:
удовлетворяет требованиям:
1.
 аналитична в полуплоскости
аналитична в полуплоскости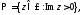 за
исключением конечного числа особых
точек
за
исключением конечного числа особых
точек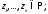
2.
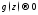 при
при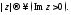
Тогда для любого
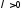 имеет место равенство
имеет место равенство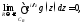 где
где полуокружность радиуса
полуокружность радиуса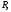 лежащая в верхней полуплоскости
лежащая в верхней полуплоскости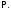
Применим эту лемму к вычислению
интеграла
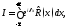 где
где
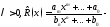 правильная
дробь (т.е.
правильная
дробь (т.е. ).
Делая те же построения, что и при
доказательстве теоремы 2, приходим к
равенству
).
Делая те же построения, что и при
доказательстве теоремы 2, приходим к
равенству
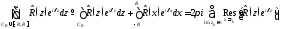
Устремляя здесь
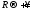 и учитывая, что согласно лемме Жордана
и учитывая, что согласно лемме Жордана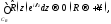 получаем формулу
получаем формулу
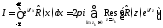

Рассмотрим примеры.
Пример 2.
Вычислить интеграл
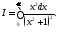
Решение. Так как подынтегральная функция чётная, то, используя формулу (2), можно записать, что

Функция
 имеет лишь одну особую точку
имеет лишь одну особую точку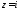 в верхней полуплоскости
в верхней полуплоскости и это есть полюс 2-го порядка. Вычет в
этой точке вычисляем по формуле (1):
и это есть полюс 2-го порядка. Вычет в
этой точке вычисляем по формуле (1):
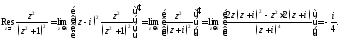
Следовательно,

Пример 3.
Вычислить интеграл


Решение. Так как подынтегральная функция чётная, то можно записать, что

Вычислим теперь
интеграл, стоящей справа, используя
формулу (3). Так как в верхней полуплоскости
функция
 имеет только одну особую точку
имеет только одну особую точку простой полюс, то
простой полюс, то
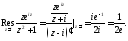
Следовательно,