
- •1.Погрешн-ть.Абсолютн и относительн.Устойчивость,корректн-ть,сходим-ть.
- •4.Решение нелинейных систем.Методы простой итерации и Ньютона.
- •5.Аппроксимация функций.Линейная и квадратичная интерполяция.
- •17.Основная лемма вариационного исчисления.
- •19.Частные случаи интегрируемости ур-я Эйлера
- •16.Экстремум ф-ала.Необходимое условие экстремума.
- •14.Непрерывность,приращение,линейность функционала.
- •11.Методы Эйлера и Рунге-Кутта для решения диффур.
- •10.Интегрирование диффура с помощью рядов и послед.Приближения
- •6.Многочлен Лагранжа и Ньютона
- •18.Простейшая задача вар.Исчисления,вывод уравнения Эйлера
- •7.Эмпирические формулы.Метод выбр.Точек,средних,наименьш.Квадратов. Необх условие сущ-я эмп.Формулы.
- •8.Численное дифф-ние ф-ции одной и нескольких переменных.
- •15.Вариация ф-ала как главная линейная часть приращения и как производная по параметру.
- •12.Краевые задачи для обыкновенных диффур,линейная краевая задача,методы конечных разностей,коллокации,Галеркина.
- •13.Понятие функционала и вариации его аргумента.Примеры.Расстояние между ф-циями и определение окрестности
- •2.Решение линейных систем, норма матрицы, вектора, понятие обусловленности. Прямые и итерационные методы решения.
- •2.Решение нелинейных.Метод деления отрезка пополам,хорд,касательных,простой итерации
1.Погрешн-ть.Абсолютн и относительн.Устойчивость,корректн-ть,сходим-ть.
При решении прикладн.или математ.задач появл-ся погреш-ти 3 типов:
Погреш-ть задачи – связана с приближенным хар-ром исх.содерж-ой модели,в частности с невозмо-тью учесть все факторы в процессе изуч-я моделир-его явл-я а так же ее математ.описания,параметрами кот.обычно служат приближ.числа, например из-за принцип.невозмож-ти выполнения абсолютно точных измерений. Для вычислителя погреш-ть задачи след.считать неустранимой(безусловной), хотя постановщик задачи иногда может ее изменить.
Погреш-ть метода(устранимая,условная) – связана со способом решения поставл.матем.задачи,появл-ся в рез-те подмены исх.матем.модели другой или конечной послед-тью других,напр. линейных моделей.При создании числ.методов закладыв-ся возмож-ть отслежив-я таких погр-тей и доведения их до сколь угодно малого уровня.
Погреш-ть округлений(действ-ая) – тип обусловлен необх-тью выполнять арифм. операции над числами,усеч-ыми до кол-ва разрядов,зависящего от применяемой вычислит.техники.
Эти 3 погреш-ти дают в сумме полную погрешность решения задачи.
Т.к. 1ый тип погр.не зависит от вычислителя,то он служит ориентиром точности,с кот.нужно решить задачу(нет смысла решать точнее чем диктует неопр.исх.данн).
Пусть А(точное) и а(приближ) близкие числа.
Величина Δа=|А-а| - абсолютная погр, величина δа=Δа/|a| - относительная
Абсолют.погр суммы равна сумме абсолют погр-ей Δ(а±в)=Δа±Δв
δ(ав)= δа+δв ; δ(а/в)= δа+δв
Отсюда видно,что относит.погр.больше,чем ближе числа х1 и х2. Пусть а=2520, в=2518 и Δа=0,5 и Δв=0,5. Тогда δа=0,5/2520=0,0002 и δв=0,5/2518=0,0002.
δ(а-в)=(Δа+Δв)/|a-в|=0,5+0,5/2=0,5
Устойчивость-задача назыв-ся устойчивой по исх.парам-ру х, если решение у непрерывно от него зависит т.е. limΔу=0 при Δх0. Отсутствие устойчив-ти означает,что небольш.погр-ть в исх.данных может привести к большой в решении или вовсе к неверному рез-ту.
Корректность-задача наз-ся поставленной корректно,если для любых значений исх.данных из нек.класса ее решение сущ-ет,единственно и устойчиво по исх.данным.Ее заменяют на основе исх.данных корректной и решают.
Сходимость-при анализе точности вычисл.процесса одним из важн.критериев явл-ся сходимость числ.метода.Она означ.близость получаемого численного решения задачи к истинному.
Пример с синусом (х) – разложить в ряд,подставить пи/6 и 8пи+пи/6 в первых три члена и сравнить значения.
Вывод: справедливость разложения тем точнее, чем ближе х к нулю. Поэтому при вычислении синус(х) аргумент следует брать от (-пи;пи) отбрасывая необх.период
4.Решение нелинейных систем.Методы простой итерации и Ньютона.
Пусть дана система нелинейных уравнений:

![]()
В отлич.от систем линейн.ур-й не сущ-ет прямых методов решения нелин.систем общего вида.Для этого обычно использ.итерационные методы
1)Метод простой итерации – если систему (1) удается представить в виде
 алгоритм
решения этой системы методом простой
итерации напоминает метод Гаусса-Зейделя
для линейных систем. Пусть в рез-те
предыдущей итерации получены значения
неизвестных х1=а1….хn=an. Тогда выражение
для неизвестных на след.итерации имеют
вид:
алгоритм
решения этой системы методом простой
итерации напоминает метод Гаусса-Зейделя
для линейных систем. Пусть в рез-те
предыдущей итерации получены значения
неизвестных х1=а1….хn=an. Тогда выражение
для неизвестных на след.итерации имеют
вид:
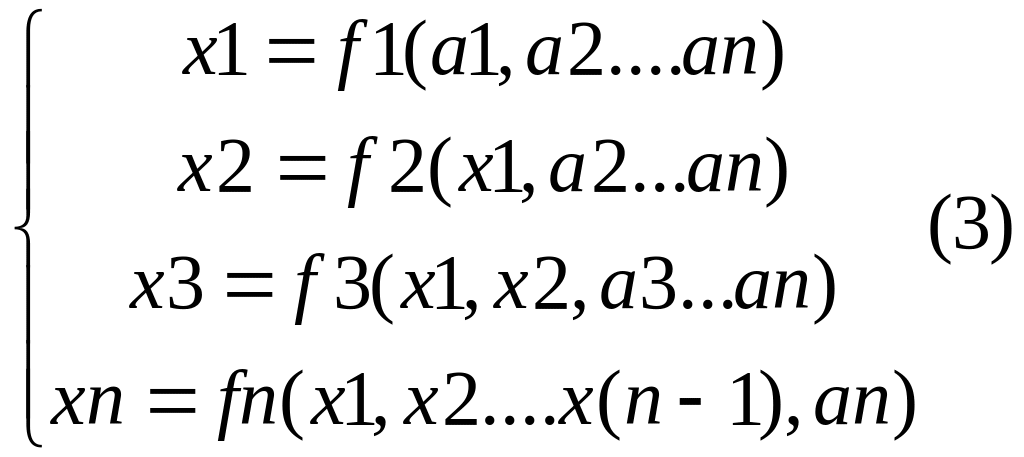 критер
STOP
на k-ой итер-и
критер
STOP
на k-ой итер-и
![]()
При исп.метода прост.итер.успех во многом опред-ся удачным выбором начальн. приближения,в противн.случае итерационный процесс может не сойтись.
2)Метод Ньютона
Пусть (a1,a2,…an) некое приближени неизв-ых (x1,x2…xn) системы (1).Поэтому ставится на кажд итер-ции улучшить решение в виде:
 отыскав поправки
(Δх1….Δxn). Для этого разложим левые части
(1) как ф-ции несколь.перем-ых с учетом
(4) в ряд Тейлора в окр.т. а1,а2,..,an, огранич-ясь
лишь первыми линейн.членами относит-но
приращений
отыскав поправки
(Δх1….Δxn). Для этого разложим левые части
(1) как ф-ции несколь.перем-ых с учетом
(4) в ряд Тейлора в окр.т. а1,а2,..,an, огранич-ясь
лишь первыми линейн.членами относит-но
приращений
![]()
………………………………………………………………………….. (5)
![]()
Поскольку левые части ур-й (1)=0 то и правые части (5)=0.

Это есть система лин.ур-й относит.неизв-ых Δx1,Δx2…Δxn.
Для сущ-я единственного решения этой системы необх.чтобы Якобиан не равнялся нулю на каждой итерации
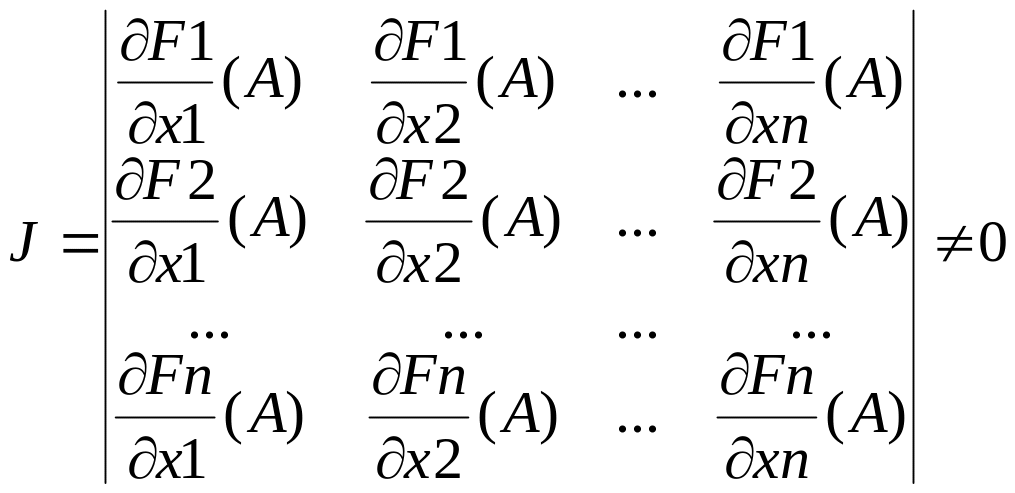
Т.о.итерац.процесс
решения системы ур-й (1) методом Ньютона
состоит в определении приращений
(поправок) Δx1…Δxn
к значениям неизвестных на каждой
итерации.Процесс прекращается если все
приращения становятся малыми по
абсолютной величине т.е.
![]()
В методе Ньютона так же важен удачный выбор начального приближения для обеспечения хорошей сходимости.
