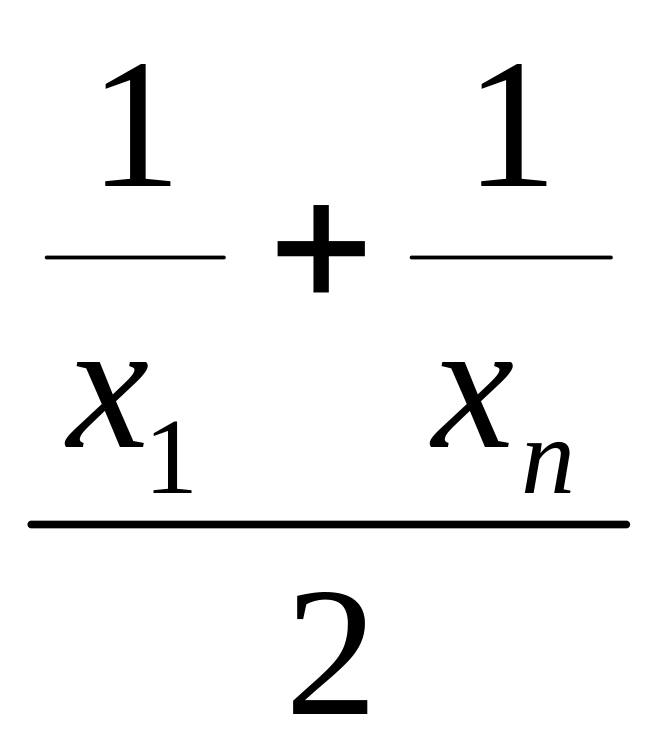7.Эмпирические формулы.Метод выбр.Точек,средних,наименьш.Квадратов. Необх условие сущ-я эмп.Формулы.

Пусть изучая неизв.функц-ю завис-ть y(x) мы в рез-те серии экспер-ов получ. табл. знач-й.Задача состоит в том,чтоб найти приближ.завис-ть y=f(x),знач-е котор.при x=x_i мало отлич-ся от опытных y_i.Построенная так образом назыв-ся эмпирич-ой.

!Задача построения эмп.формулы отлич-ся от задачи интерпол-я тем,что график эмп.завис-ти вообще говоря не проходит через узлы (x_i;y_i) что приводит к сглаживанию эксперим.данных,а интерполяц.формулы повторила б все ошибки, имеющ-ся в экспер-те.

Построение эмп.формулы состоит из 2 этапов:

1)Подбора общ.вида этой формулы 2)Определение наилучш.значений содержа-ся в ней параметров.

Общ.вид формулы иногда известен из физич.соображений(бросок камня парабола)

[I] Простейш.эмп.ф-ой явл-ся линейная зависимость y=ax+b близость экспер-ого распред-я точек к линейн.завис-ти легко просматр-ся после построения графика. Можн сделать проверку k≈∆y_i/∆x_i - const, точность такой аппрокс-ции опред-ся отклонением величин k_i от константы.

[II] Степенная зависимость y=cx^α (c>0) она может быть сведена к линейной:

y=cx^α (c>0) lgy=lgcx^αlgy=lgc+αlgxlgy=y’, lgx=x’, lgc=b, α=a, y’=ax’+b

Т.о.степенная завис-ть между переменными x и y обнар-ся если перем-е lgx_i и lgy_i удовл-ют линейной зависимости.

[III] Показательная зависимость y=ce^αx (c>0) так же сводится к линейной: lny=lnc+ax  y’=lny, lnc=b  y’=ax+b. Т.о.показ.завис-ть между переем-ми x и y обнар-ся если точки x_i и lny_i лежат на 1ой прямой.

[IV] Гиперболическая зависимость y=1/(ax+b)  1/y = ax+b Т.о. гиперболич.зав-ть между x и y обнаруж-ся,если точки xi и 1/yi имеют линейн.завис-ть.

Для опред-я параметров эмпирич.формулы сущ-ют след.методы:

Метод выбранных точек – пусть для системы опыт-х точек M_i(x_i;y_i) выбрана эмп. формула y=f(x,a₁,a₂….a_m) с m неизв.парам-ми. На корд.плоск-ти x0y провод-ся плавная кривая Г,опис-я точки m_i.На Г выбир-ся система из m точек N_j(x_j,y_j), тогд желат-но,чтоб точки N_j были по возможн.равномерн распред-ны по всей рабоч. части кривой Г и возможн дальше отстояли др от др и от малонадежных концевых.

Парам-ры (a₁,a₂….a_m) в общ.случае могут быть определены из m-уравнений

Метод средних-если в эмпирич.формулу y=f(x,a₁,a₂….a_m) (*) подставить исх.данны Mi(xi;yi) то лев.часть формулы вообще говоря не будет равна правой y_i≠f(x_i,a₁,a₂….a_m). Разности или невязки ε_i=f(x_i,a₁,a₂….a_m)-y_i назыв-тся уклонен-ми и представ-ют собой расстояния по вертикали точек Mi от графика эмпир.формулы (*) взятой со знаком «+» или «-». Согласно методу средних за наилучш.положение эмпирич.кривой Г приним-ся то,для кот.равна нулю алгебраич.сумма всех невязок.

Для опред-я по методу средних m неизв-ых парам-ов (a₁,a₂….a_m) все уклонения ε_i разбивают на m групп,содержащих примерно одинак.кол-во уклонений.Приравн-я к 0 алгебр.сумму уклонений,входящ.в кажд.из этих групп,получ систему,содерж. столько ур-й,сколько имеем неизв-ых парам-ов.

!Рез-ты метода сред-х сущ.зависят от способа группировки уклонений.Наиб.удачн. эмпир.формулы получ-ся если уклон-я групп-ся последов-но и каждая группа содержит их примерно один.кол-во членов.

Метод наименьш.квадратов –пусть известен вид эмпир.формулы y=f(x,a₁,a₂….a_n) и ε_i=f(x_i,a₁,a₂….a_n)-y_i – уклон-я эмпирич.формулы от (xi;yi).Согласно методу наим.кв наилучш.коэф-ми a₁,a₂….a_n считаются те,для кот.сумма квадратов уклонений будет минимальной S(a₁,a₂….a_n)= отсюда исп-я необх.усл. экстремума ф-ции нескольк.перем-ых S(a₁,a₂….a_n) получаем так назыв-ю нормальн систему для опред-я коэф-ов a_i Если система имеет единст.решение,то оно будет искомым.

!Метод обладает преимущ-ом,что если сумма S квадратов уклонений ε_i мала,то сами эти уклон-я также малы по абсолют.величине.Для метода средних,где составл-ся алгебраич.сумма уклонений,такого вывода сделать нельзя.

Необходимое условие существования эмпирической формулы:

Пример: y=ax^b, где x_i>0 , y_i>0. Возьмем и подставим в формулу

Т.о.для сущ-вания завис-ти y=ax^b необх.чтоб среднему геометрич. x_s знач-й x₁,x_n соответ-ли среднему геометрич-му y_s знач-я y₁,y_n т.е.если x_i образует геометрич. прогрессию,то значения y_i так же должны образовывать геометрич.прогрессию.

Строим таблицу:

xs
ys
формула	y=ax+b	y=axb	y=abx y=aebx	y=a+b/x	y=1/(ax+b)

20.Ф-алы,завис-е от нескольких ф-ций.от произв.высших порядков.Ур-е Эйлера-Пуассона.

J[y₁,y₂….y_n]= при заданных краевых условиях:

y₁(a)=A₁ y₁(b)=B₁

y₂(a)=A₂ y₂(b)=B₂

…………. …………

y_n(a)=A_n y_n(b)=B_n

Будем варьир-ть лишь 1 из ф-ций y_j(x) (j=1,2,3…n) оставляя все остальн.ф-ции неизм,при этом ф-ал J[y₁,y₂….y_n] превр-ся в ф-ал,завис-й лишь от 1ой варьир.ф-ции y_j(x) т.е. ф-ал,рассмотренный выше,след-но ф-ция y_j(x) реализ-яя экстремум,должна удол-ть ур-ю Эйлера т.к это рассуждение применимо к любой ф-ции y_j(x) то мы приходим к системе ур-й Эйлера определ-их вообщ говоря 2n-парам-ое семейство интегр. кривых.Если в частности ф-ал зависит лишь от 2 ф-ций

y(a)=A₁; z(a)=A₂; y(b)=B₁; z(b)=B₂т.е. знач-е ф-ала опред-ся выбором простран-ой кривой,получ-ой пересеч-ем 2х цилиндрич.поверх-ей,направляющими кот.служат кривые y=y(x) и z=z(x).Варьируя тольк y(x) и фиксир.z(x) мы изменим нашу криву так,что ее проекц на x0y не измен-ся,тоесть кривая все время остается на проектирующем цилиндре z=z(x).Аналогичн наоборот,получаем при этом систему ур-й Эйлера:

Ф-ал от произв.более высокого порядка:исслед.на экстрем.ф-ал

где F будем считать дифф-ой по всем своим арг-там. Гранич.усл.имеют вид: y(a)=A₀, y’(a)=A₁, y’’(a)=A₂… y^(n-1)(a)=A_n-1

y(b)=B₀, y’(b)=B₁, y’’(b)=B₂… y^(n-1)(b)=B_n-1

т.е.в гранич.точках заданы знач-я не только ф-ции,но и ее произв-х до порядка n-1 включит.Предположим,что экстремум достиг-ся на кривой y=y₀(x)ϵC_2n[a;b],дадим y₀(x) нек.приращение δy=δy(x) такое,чтоб приращ.точка осталась в рассм.множ-ве.

y₀(x)+δyϵC_2n[a;b] ; y(x)=y₀(x)+δy и чтобы для новой кривой выполнялись граничн.усл-я: δy(a)=0; δy’(a)=0; δy’’(a)=0….; δy^(n-1)(a)=0

δy(b)=0; δy’(b)=0; δy’’(b)=0….; δy^(n-1)(b)=0

Кривую y(x)=y₀(x)+δy называем кривой срав-я.Применим теорему к ф-лу и получи

Интегрируя второе слагаем.по частям,третье 2 раза по частям и т.д. будем получать

вынесем за скобку: Т.к. δy(х) произв-я ф-ция,удовл-я лишь условиям(выше),то 1ый множ-ль под знаком интегр.явл-ся непрерывн.ф-цие от х в силу основн.леммы вар.исчисл. на экстремум y0(x) 1ый множ-ль тожд.=0

т.е. ф-ция y=y(x) реализ-яя экстрем-ли ф-ала должна быть решением диффура порядка 2n.Этот дифур Эйл-Пуассона,а его инт.кривые наз-ся экстремалями рассм.вар.задачи.То ж самое для (z) повторить и тогда ф-ции y(x) и z(x) долж.удовл-ть системе ур-й Эйлера-Пуассона,так же для любого числа ф-ций.

9.Численное интегрирование.Методы прямоуг.и трапеций,Симпсона,Монте-Карло

Пусть на отрезке [a;b] задана ф-ция y=f(x) с пом точ a=x₀,x₁,x₂…x_i-1,x_i,x_i+1…x_n=b. Разобьем на n элемент.отрезков.На кажд отр.выберем произв.точку s_i и сост.сумму ее предел есть опред.интеграл.

1)Метод прямоугольников:исп-ся замена опред-го интеграла инт.суммой,где в точке ξ_i могут выбир-ся:

1.Левые границы элем.отрезков: будет получ-ся: (картинка с кривулькой и прямоугольниками внутри)

2.Правые концы (крив с кВ наружу)

3.Середины элем.отрезков:

2)Метод трапеций:исп-ют линейн.интерп-цию,т.е.ф-ция y=f(x) представ-ся в виде ломаной,соедин.точки x_i;y_i: если шаг const то формула приобр.более простой вид:

!Когда подынт.ф-ция задана в аналит.виде,опред-ый инте-л удается вычислить непосред.с пом.неопред.инт-ла(первообр) по ф-ле Ньютона-Лейбница: однако на практике этой фор-ой часто нельзя восп.по 2 причи-м:

• Вид f(x) не допуск.непосред.инт-я т.е.первообр.нельзя выр-ть в элем ф-циях.

• Знач-е f(x) заданы только таблично.

В 1ом случае ф-цию представл.в виде ряда Тейлора и инт-ют несколько членов,во втором строят интерпол.многочлен и интегрируют.

3)Метод Симпсона:разобьем отрезок инт-я [a;b] на четное число n равных отрезков с шагом h.Подынт.ф-цию f(x) заменим на отрезки [x_i-1;x_i+1] интерпол-м многочл. 2ой степени:φ_i(x)=a_ix²+b_ix+ci, в кач-ве φi(x) можно принять интерп-й многочлен Лагранжа 2ой степени,проходящ.через точки: M_i-1(x_i-1;y_i-1),M_i(x_i;y_i),M_i+1(x_i+1;y_i+1)

Элемент.площадь Si может быть вычислена с пом.опред.интеграла

Суммируя получен выраж-я,получ: получим ф-лу Симпсона:

4)Метод Монте-Карло:Пусть x равномер.распред.случ.величина на [a;b].Это означ. что ее плотность распред-я задается соотношением: 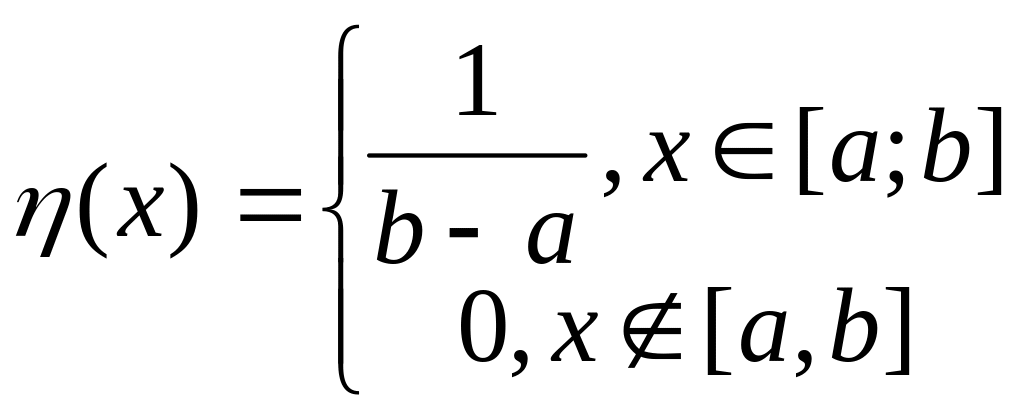тогда ее матожидание Пусть на [a;b] задана непрерыв.ф-ция f(x).Тогда если x случ.велич.то f(x) тоже случ.велич,причем если x равномерн.распред.на [a;b] то и f(x) равномер.распред.на [a;b] т.е.

Пусть x_i дискретное множество значений,где x_iϵ[a;b]. Тогда f(x_i) так же некоторая совокуп-ть знач-й или выборка. Тогда матожидание: Очевидно что M(f(x))≈M(f(xi)) и тогда интеграл