13.Понятие функционала и вариации его аргумента.Примеры.Расстояние между ф-циями и определение окрестности

Пусть дано нек.множ-во M{y(x)} ф-ций.Если кажд ф-ции ф-ции y(x)ϵM по некотор закону поставлено в соотв-е опред.число J,то говорят,что на множ-ве M опред-н ф-ал J и пишут J=J[y(x)].Множ-во М ф-ций y(x) наз-ся обл.опред-я.

Пример: M=C[0;1],J[y(x)]= то знач-е ф-ала в этой ф-ции:

Опр:Вариацией(приращ-ем) δy аргумента y₀(x)ϵM ф-ала J=J[y(x)] назыв-ся разность между двумя ф-циями y(x)-y₀(x),где y(x)ϵM.

Если ф-ция получ.приращ. δy то ее произв.получает приращ. δy’ и т.д.Говорят что кривые y=y₁(x) и y=y₂(x),заданные на [a;b] близки в смысле близости нулевого пор-ка если мал |y₁(x)-y₂(x)| xϵ[a;b],геометр.это означ.что они близки по ордината.

Говор,что кривые близки в смысле близ-ти 1го порка если малы |y₁(x)-y₂(x)| и |y’₁(x)-y’₂(x)|.Геометр.они близки по ординатам и по направлениям касательных в соотв.точках.

Опр:расстоянием 0го порка между кривыми заданными на [a;b] назыв-ся неотриц. число ρ0 равное максимуму модуля ρ₀= ρ₀(y₁(x);y₂(x))=max| y₁(x)-y₂(x)|

Пример:найти расстояние 0го порка между кривыми y=x и y=x² на [0;1]:

ρ₀(x;x²)= max|x-x²|=max(x-x²), f(x)=x-x², f’(x)=1-2x=0, x=0,5, f(0,5)=0,5-0,75=0,75.

Опр:ε окрестностью kго порка кривой y0(x)ϵCk[a;b] называется совокупность всех кривых y(x)ϵCk[a;b],расстояние k-го порядка которых от кривой y₀(x) меньше ε.

! ε окр нулевого порядка кривой y₀(x) состоит из всех кривых y(x)ϵ[a;b] , расположенных в полюсе ширины 2ε вокруг y₀(x)

2.Решение линейных систем, норма матрицы, вектора, понятие обусловленности. Прямые и итерационные методы решения.

Опр:нормой матрицы(вектора) А наз-ся действ.число ||A||,удовл.условиям: ||A||≥0, ||λA||=λ||A||, ||A+B||≤||A||+||B||.Лин.пространство Rn с введенной в нем нормой наз. нормированным.Понятие длины или модуля вектора удовл-ет этим аксиомам. Нормой вектора имеет право наз-ся 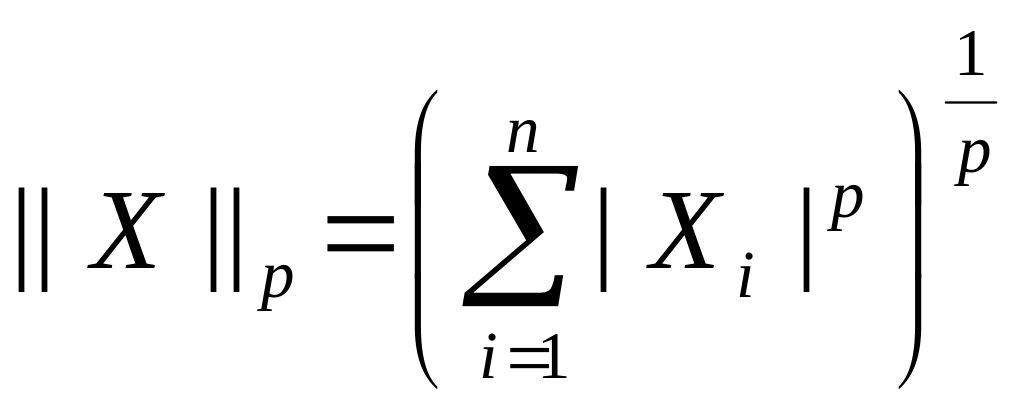где pϵ[1;+8],Xi-компоненты вектора X.Это норма Гёльдера,при p=2 Евклидова,при бесконеч-норма максимум. Условие согласованности: ||AX||≤||A||*||X||

Опр:норма матрицы А наз-ся подчиненной норме n-мерного вектора Х,если она задана равенством ||A||=max||AX|| (X=1)

Опр:положительное число ||A||*||A^-1|| называют числом(мерой) обусловленности матрицы А и обозначают ||A||*||A^-1||=condA.

!Чем больше число обусловленности,тем сильнее сказыв-ся на реш-и линейной системы ошибка в исх.данных.

Прямые методы исп.конечн.соотн-я(формулы) для вычисл-я неизв-ых,дают решение после вып-я заранее известного числа опер-й.Методы универсальны.

Недостатки: треб.хран-я в опер.памяти ЭВМ сразу всей матрицы,не учитывают структуру матрицы при больш.числе нулевых элем-ов,сильно скаплив.погрешн-ти в процессе реш-я.

!Исп-ся для небольш.n<200 систем с плотно заполн.матрицей и неблиз.к нулю опред-ем.Иногда их наз-ют точными,поскольку реш-е выраж-ся в точных формулах через коэф-ты системы.Но точн.реш-е может быть получ.только при работе с бесконеч.числом разрядов,чего на практике достичь нельзя.

Итерац.методы-методы послед-ых приближений,в них необх.задать некот.прибли решение-начальное приближение.После этого с помощью алгоритма проводится 1 цикл вычислений(итерация).В рез-те итерации находят новое приближение. Итерац методы об.сложнее и их объем сложно предсказать.Погрешность не скаплив-ся.

!Итер.методы могут исп-ся для уточнения решений,получ.с пом-ю прямых методов,комбинирование эффективно.

Итерац.метод Гаусса-Зейделя: на примере системы
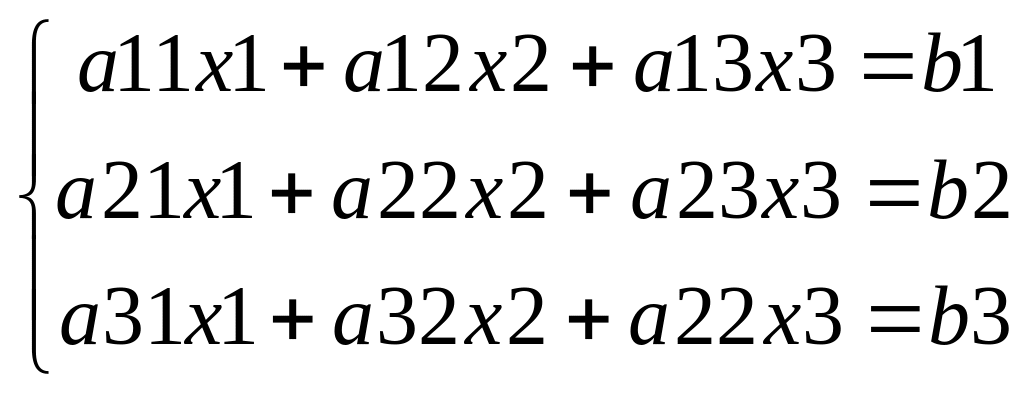