19.Частные случаи интегрируемости ур-я Эйлера

Ур-е Эйлера не всегда инт-ся легко,т.к.дифуры 2го пор.инт-ся в конечном виде в исключ.случ-х.Рассмотр.нек.частн.случ.инт-ти ур-я Эйлера:

1)F не зависит от y’ : F=F(x;y),тогда ур-е Эйлера имеет вид: F'_y=0

Решение y=f(x) получ-го недифф-го ур-я не содержит произв.констант и поэтому вообще не удовл.граничн.условиям y(a)=A и y(b)=B.Следов-но решение рассматр. вариац.задачи вообще говоря не сущ-ет.Лишь в исключ.случ-ях,когда кривая y=f(x) проходит через точки (a;A) и (b;B) сущ-ет кривая,на кот-ой может достиг-ся экстремум,например: решение y(x)=1/x будет решением простейш.задачи вар.исчис-я только в том случ-е,если гранич.усл-я имеют вид y(1)=1 и y(2)=1/2.В противн.случ-е найден.реш-е ур-я Эйлера не явл-ся экстрем-ю вариац.задачи.

2)Ф-ция F линейно зависит от y’ : F=M(x;y)+N(x;y)y’ т.е. Если окаж-ся,что по теореме о незав-ти криволин.интеграла от пути интегрир-я,вариац-я задача теряет смысл т.к. интеграл по люб.кривой,соедин-ей данные точки (a;A) и (b;B) один и тот же.В противн.случ.можн составить ур-е Эйл.

;

Это о5 как и в прошл.случ.недифф.ур-е

3)Ф-ция F зависит лишь от y’: F=F(y’) ур-е Эйлера примет вид поэтомуy’’=0 или первое ур-е имеет решение: y=C₁x+C₂-это двухпарам-кое семейство прямых.Если 2ое ур-е имеет один или несколько действит.корней,то

F”_y’y’(y’)=0, y'=k_i=>y-k_ix+C_i то мы получ.однопарам-ое семейство прямых,кот. содержится в получ-ом двухпарам-ом семействе,например реш-ем будет y=C1x+C2.Данный ф-ал выраж-ет длину дуги кривой,а знач.кратчай расстояние между точками (a;A) и (b;B) будет отрезком прямой.Оно будет найдено из общего решения через граничн.условия y(a)=A ; y(b)=B.

4)Ф-ал F зависит лишь от x и y',т.е. F=F(x;y’), ур-е Эйлера вида и следов-но 1ый интеграл будет найден F'_y'(x;y')=C₁ Причем т.к.получ-е ур-е первого порядка не содержит y,то может быть проинт-но иным путем непосред-но разрешения относит-но y' или путем введения парам-ра y'=tgt,например: т.е.ур-е примет вид: .Для реш получ-го дифура 1го пор-ка выразим y'.

5)Ф-ал F зависит лишь от y и y’ т.е F=F(y(x);y’(x)),запишем ур-е Эйлера

,запишем в развернут.виде

то лев часть превр-ся в произв-ю

Т.к. это ур-е уже 1го порядка не содержит явно x то оно м.б. проинтегр-но путем разреш-я относит-но y' и раздел-я перем-ых или путем введения параметра.

16.Экстремум ф-ала.Необходимое условие экстремума.

Ф-ал J[y(x)],заданный в лин.пространстве C_k[a;b] достигает на прямой y=y₀(x) маx(min) если найдется εокр точки y₀(x),что для всех кривых ¥y=y(x)ϵO_ε(y₀(x)) выполн-ся нерав-во:

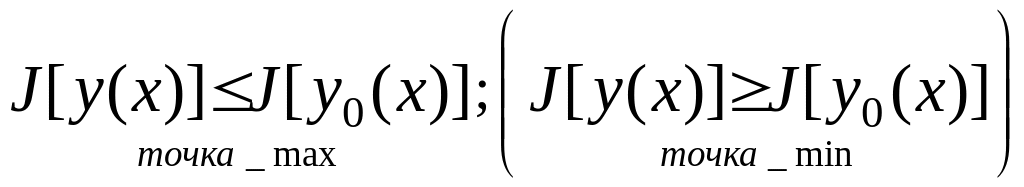
Теорема:Необходимое условие экстремума функционала

Если ф-ал J[y(x)] имеющ.вариацию в нек.окр.точки y=y₀(x) достигает на ней макс или мин,то δJ[y₀(x)]=0.

Док-во: при фиксированных y₀(x) и δy ф-ал J[y₀(x)+αδy]≤J[y₀(x)] (пусть для опр-ти y₀(x) точка max).

Выражение: J[y₀(x)+αδy] при фиксир-ых y₀(x) и δy явл-ся функцией от α:

J[y₀(x)+αδy]=φ(α) которая при α=0 по условию достигает максимума,следов-но производная в этой точке должна быть равна 0 как необходимое условие экстремума ф-ции одной переменной φ’(0)=0 то есть

Итак на кривых,на которых достигается экстремум ф-ала,его вариация равна нулю.

Опред:экстремум ф-ала на все области определения называется абсолютным.

Опред:ф-ции для которых δJ=0 будем называть стационарными.