5.Аппроксимация функций.Линейная и квадратичная интерполяция.

у	y1	y2	…	yi	…
х	x1	x2	…	xi	…

Пусть велич. у явл-ся ф-цией от х.

Известны лишь некот.значения

Т.е.дискретному множеству xi поставлено в соответствие дискретное множество уi.Став-ся задача опис-я знач-я ф-ции y в др.точках,отличных от узлов xi.Этой цели и служит задача о приближ-и (аппрокс-ии) ф-ции,заданной дискретно(таблично).Если приближ-е строится на зад-ом дискретном множ-ве точек xi,то аппрокс-я назыв-ся точечной.

1)Простейш. и част.использ-мым видом локальн.интерполяции явл-ся линейная. Она состоит в том,что заданные точки (хi;уi) соедин-ся прямолин.отрезками и ф-ция f(x) приближ-ся(аппрокс-ся) ломаной с вершинами в данных точках.Урав-я кажд.отрезка ломаной в общем случ.разные.В частн-ти для i-го интервала можно написать ур-е прямой,проходящ.через точки (x_i-1;y_i-1),(xi;yi)

откуда y=a_ix+b_i где xϵ[x_i-1;x_i],

Т.о.при использ-ии линейн.интерпол-ии сначала нужно опред-ть интервал,в кот. попадает аргумент х а затем построить уравнение прямой по 2 точкам-концам этог интервала, и найти значения у от х.

2)Квадратичная интерполяция y=ax²+bx+c.В кач-ве интерп-ой ф-ции на отрезке [x_i-1;x_i+1] применяется квадратный трехчлен.Такую интерп-ю назыв.параболич-ой.

Ур-е квадр.трехч-на на отрезке [x_i-1;x_i+1] содержит 3 неизв.параметра a,b,c

y=a_ix²+b_ix+c_i для опред-я кот-ых нужны 3 ур-я.Ими служат условия прохождения параболы через 3 точки,кот.можно записать в виде:

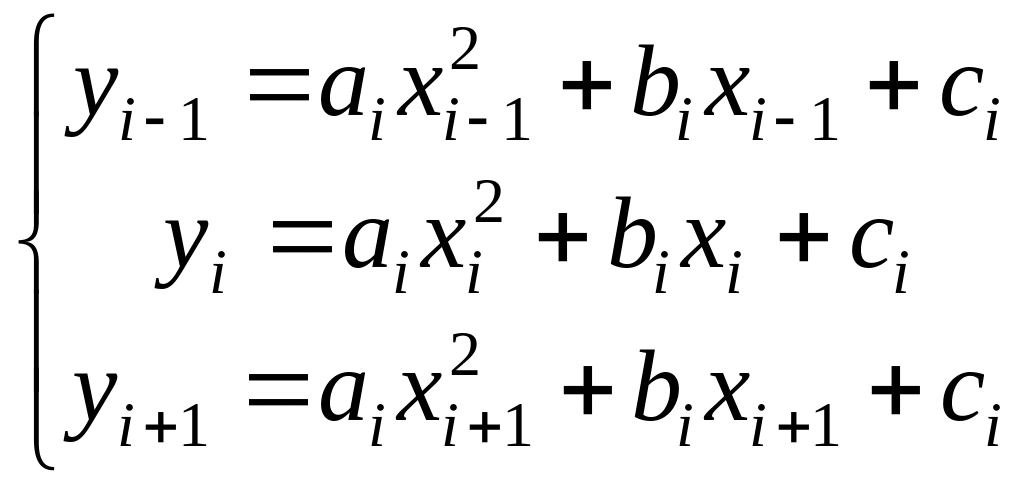
Решая систему лин.ур-й относит-но ai,bi,ci мы найдем коэф-ты квадратного трехч. Перейдем к случ.глобальн.интерпол-ции,т.е.построению интерполяц.многочлена, единого для всего отрезка [x₀;x_n].При этом график интерпол.многочлена должен проходить через все заданные точки.Запишем иском.многочл.в виде

. Из условий равенства этого многочлена в узлах xi соответствующим знач-ям yi получим систему линейн.ур-ий для нахожд.коэф-ов a₀,a₁,a₂…a_n.Очевид.что эта система имеет единств.реш-ие,если среди узлов интер-и

нет совпадающих.

!такой пусть построения интерпол-ого многочлена требует значительного объема вычислений,особенно при большом числе узлов.

17.Основная лемма вариационного исчисления.

Если для кажд.непрерывн.ф-ции η(х) где f(x) непрерыв-я на [a;b] ф-ция,то f(x)≡0 на [a;b].

Док-во методом от противного:

Предположив,что Ӡcϵ[a;b] такое что f(c)≠0, получим наличие некоторой окрестности (c-δ;c+δ) в которой f(x) сохраняет знак числа f(c).Но тогда выбрав η(х) так же сохраняющей знак в этой окрестности и равной 0 вне этой окрестности получим

Мы пришли к противоречию,значит предположение было неверно,а верно,что при

f(x)=0, т.е. f(x)≡0.

!Замечание1:утверждение леммы и ее док-во не изменятся,если на ф-цию η(x) наложить ограничения η(a)=η(b)=0 и η(x) имеет непрерывные производные до порядка p.

!Замечание2: ф-цию η(x) можно выбирать,например так где nϵN, kϵR.

Очевидн,что ф-ция η(x) удовл-ет упомянутым выше условиям.Она непрерывна, имеет непрерывные произв-е до пор-ка 2n-1,обращ-ся в нуль в точках a и b и может быть сделана сколь угодно малой вместе со своими производными за счет уменьшения множителя k.

!Замечание3: Аналогично можно доказать,что если ф-ция F(x;y) непрерывна в обл D плоск-ти xOy и при произв-ом выборе ф-ции η(x) удовлетворяющей лишь некоторым условиям (непрерыв-ть,дифферен-ть,обращение в нуль на границе области D,то F(x;y)≡0 в области D.

Ф-цию η(x;y) можно выбрать так

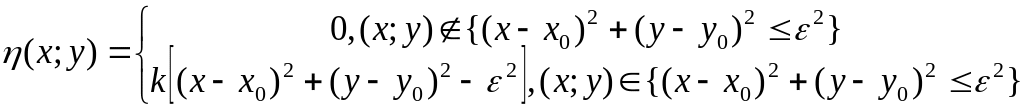
Т.о. лемма справедлива для n-кратных интегралов.