8.Численное дифф-ние ф-ции одной и нескольких переменных.

при числ.дифф-ии бесконеч.малое ∆x заменяют на некотор.конечн.число и для вычисл-я знач-я производной получают приближ. равенство: y'≈∆y/∆x.Это соотнош.назыв-ся аппроксимацией произв-ой с помощю отношения конечн.разн-тей ∆y и ∆x.Пусть ф-ция задана таблично.Пусть разность между соседн.знач-ми аргументы(шаг) постоянн.и равно:h=x₁-x₀=x₂-x₁… Если хотим найти y'(x₀)=y'₀: ; ; не делают предельный переход.В завис-ти от способа вычисл.конечн.разностей получ разные фор-лы для вычис-я произв-ой в данной точке:

(1)Левые разности: ∆y₁=y₁-y₀; y’₁=(y₁-y₀)/h (2)Правые: ∆y₁=y₂-y₁; y’₁=(y₂-y₁)/h

(3)Центральные разности: ∆y₁=y₂-y₀; y’₁=(y₂-y₀)/2h Можно найти выр-е для старш произв-ых:

Рассмотр.ф-цию 2х перем-ых U=f(x;y) заданную в табл.виде U_ij=f(x_i;y_j) где x_i=x₀+ih₁ (i=0,1,2…I) ; y_j=y_o+jh₂ (j=0,1,2…J)

Задана таблично т.е.задана матрица.

Записывая разлож.в ряд Тейлора при разных знач-ях ∆x ∆y можн вывести фор-лы числ.дифф-я с необх.порядком точности аппр. Приведем оконч.фор-лы(шаблоны)для нек.аппрокс.частных произв-х:

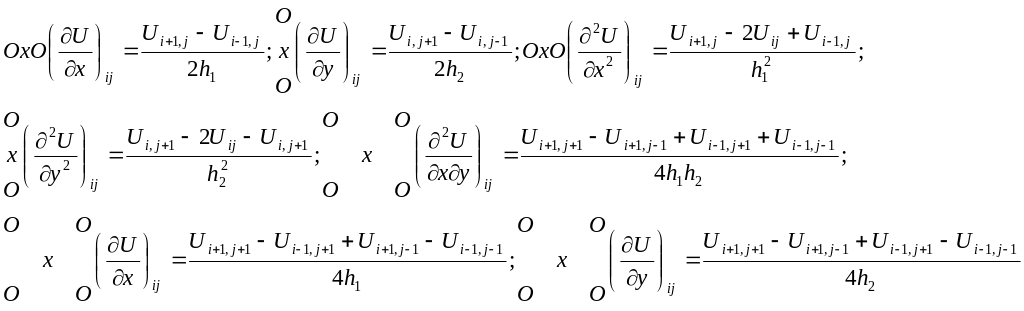
15.Вариация ф-ала как главная линейная часть приращения и как производная по параметру.

Опр: если приращение ф-ала в точке y₀(x) из C_k[a;b] ∆J=J[y₀(x)+δy]-J[y₀(x)] можно представить в виде: ∆J=L[y₀(x);δy]+β(y₀(x);δy)*max|δy| где L[y₀(x);δy] – линейный по отношению к δy функционалу, β(y₀(x);δy)0 при max|δy|0 то линейная по отношению к δy часть приращения ф-ала т.е. L[y₀(x);δy] называется вариацией функционала и обозначается δJ. Итак,вариация функционала – это главная линейная по отношению к δy часть приращения функционала.При исследовании функционалов вариация играет такую же роль,какую играет дифференциал при исследовании функции.

Опр: Вариацией функционала J[y(x)] в точке y=y0(x) называется значение производной фунционала J[y0(x)+αδy] по параметру α, когда α=0

12.Краевые задачи для обыкновенных диффур,линейная краевая задача,методы конечных разностей,коллокации,Галеркина.

Рассмотр.диффур n-го пор-ка F(x1;y;y';y'';…;y(n))=0 (n≥2).Краев.задача для дифура заключ-ся в:найти решение y=y(x) ур-я,для кот.знач-я его произв-х в точках x_i: y_i^(s)=y^(s)(x_i) {x_i} удовл-ют n-независимым между собой краев.условиям.

Простейш.двухточечн.краевая задача заключ.в: найти ф-цию y=y(x),удовл-юю диффура 2го пор-ка y''=f(x,y,y') и принимающую при x=a,x=b заданные значения: y(a)=A,y(b)=B.Геометрич.это означ.что треб.найти интегр.кривую-решение,проход через точки (a;A) (b;B), Найти такое реш-е y=y(x) чтобы y'(a)=A₁,y'(b)=B₁, геометр эта задача свод-ся к отысканию инт.кривой дифура,пересек.прямые в точках x=a и x=b под задан.углами α,β такими,что tgα=A₁,tgβ=A₂ т.е.задано знач-е скоростей процесса.Смеш.задача-когда иском.решение y(x) удовл.услов-м y(a)=A и y'(b)=B₁ т.е. треб.найти инт.кривую,проход.через задан.точку (a;A) и пересек.прямую под задан.углом.

Опред:Если диффур и краевые условия линейны,то краевая задача наз.линейной.

P_n(x)y⁽ⁿ⁾+P_n-1(x)y^(n-1)+…+P(x)y’+P₀(x)y=f(x) сокращен можн запис.в виде L[y]=f(x) здесь P_i(x) и f(x)-известные непрерывные на отрезке [a;b] ф-ции

Опр:если в краев.усл-я входят 2 абсциссы x₁=a, x₂=b концы отрезка [a;b] то такие условия называют двухточечными.

Опр:краев.усл-я называются линейными если они имеют вид R_j[y]=γ_j (j=1,2…n) где где заданные const причем j-номер условия.Например,краевые условия из примера линейны т.е.их можно записать в виде: где αβγϵR

!Если для дифура 2го пор-ка краевые условия имеют вид то они назыв. условиями периодичности.

Метод конечных разностей:на примере лин.дифура 2го пор-ка с двухточ.краев усл-ми. p(x),q(x), f(x)-непрерывн.на [a;b].Сводим к системе конечноразностн.ур-й.Разобьем [a;b] на n равных частей, (b-a)/n=h точки разбиен.имеют абсциссы x₀=a,x_i=x₀+ih (i=1,2…) ,x_n=b.Введем обознач-я y_i=y(x_i);y'_i=y'(x_i);y'_'i=y''(x_i), P_i=P(x_i), q_i=q(x_i), f_i=f(x_i) тогда

для всех i=1,2,3…n-1

Метод коллокации:дает возмож-ть найти знач.е краевой задачи в виде аналит. выражения.Пусть треб-ся опред-ть ф-цию y=y(x) удовл-юю линейному дифуру

L[y]=y’’+p(x)y’+q(x)y=f(x) и линейным крае.усл-ям Гa[y]=α₀y|a|+α₁y’|a|=A

Гb[y]=β₀y|a|+β₁y’|a|=B Выберем нек.совокуп.нек.линейн.независ.ф-ций U₀(x), U₁(x)…U_n(x) – базисные,из кот.ф-ция U₀(x) удовл-ет соотв.неоднор.краевым усл-ям: Га[U₀]=A, Гb[U₀]=B а остальн.Ui(x) удовл-ют соотв-им однор.краевым.усл-ям

Га[U_i]=0, Гb[U_i]=0. Будем искать приближ.решение краев.задачи в виде линейной комбинации базисных ф-ций тогда ф-ция y удо-ет краев.усл-ям тоесть подставляя получим выр-е R(x,C₁,C₂..C_n)≡L[U0]+ Если при нек. выборе коэф-ов {Ci} выполн.равенство R(x,C₁,C₂..C_n)≡0 то ф-ция y(x) явл-ся точным реш-ем задачи.Однако подобрать так точно коэф-ты Ci невозм-но,поэтому огранич-ся тем,что требуют,чтобы ф-ция R(x,C₁,C₂..C_n) обращалась в нуль в задан системе точек x1,x2,x3…,xnϵ[a;b]-это точки коллокации в кот.равенство будет вып. точно 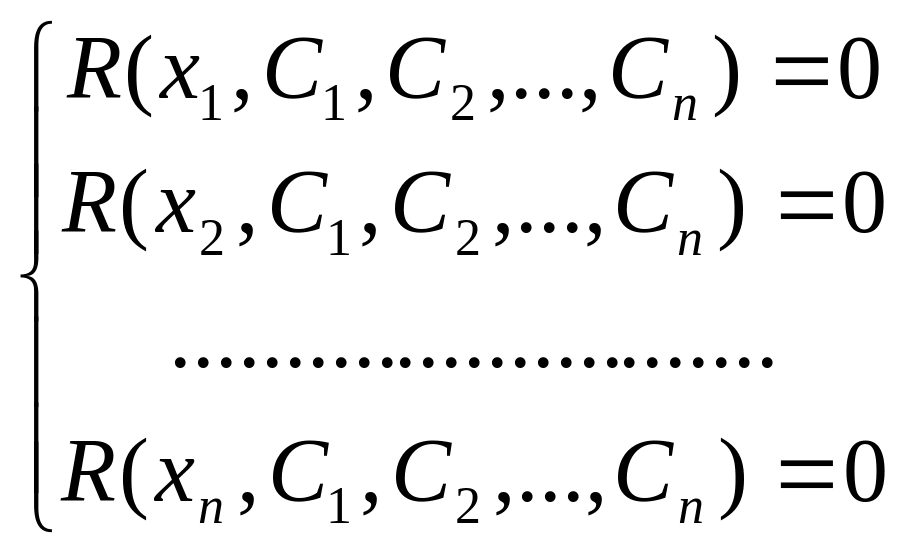в рез-те получаем систему лин.ур-й,из кот.находим коэф-ты (C₁,C₂,…C_n),после чего приближ.решение задачи задается формулой

Метод Галеркина:Теорема:Пусть {Un(x)} полная система ф-ций с ненулевой нормой,ортогон.на [a;b],если непрерывн.ф-ция f(x) ортогон-на на [a;b] ко всем Un(x) ф-циям т.е. то f(x)≡0 при Ɏxϵ[a;b],поэтому чтобы невязка R(x,C₁,C₂,…C_n) была мала (R≈0) согласно методу Галеркина потреб.чтобы невязка R была ортогональна к базисным ф-циям Ui(x),что при достаточном числе этих ф-ций обеспеч.малость невязки

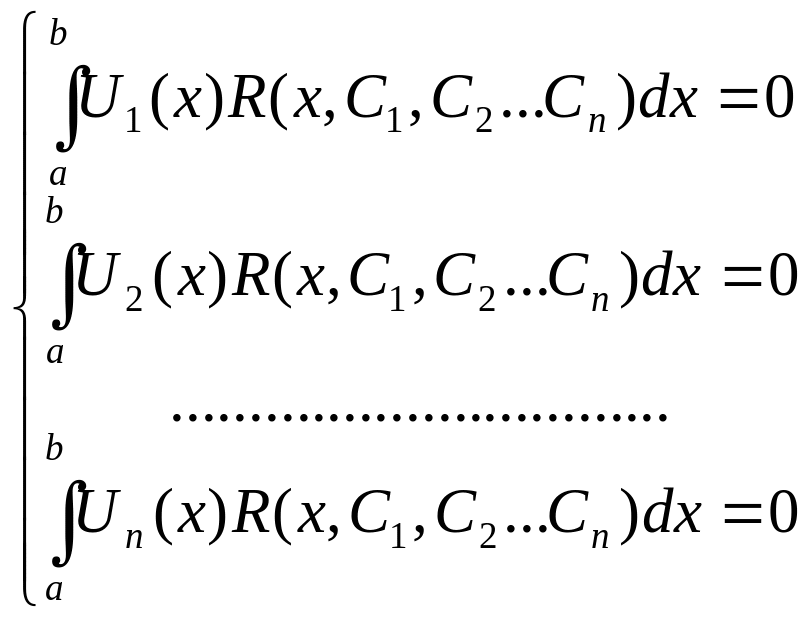Из этой системы определяем неизв.коэф-ты С₁,С₂…С_n