
- •3 Семестр (часть 1). Дифференциальные уравнения
- •1. Общие понятия
- •3. Дифференциальные уравнения с разделяющимися переменными. Однородные уравнения
- •1. Линейные дифференциальные уравнения. Метод вариации произвольной постоянной
- •2. Задача Коши. Теорема существования и единственности решения задачи Коши. Общее решение и общий интеграл
- •3. Уравнения, допускающие понижение порядка
- •1. Свойства дифференциального оператора. Теорема Коши
- •2. Линейная зависимость и линейная независимость системы функций. Вронскиан. Исследование линейной независимости с помощью вронскиана
- •3. Структура общего решения однородного дифференциального уравнения
- •Лекция 4. Общее решение неоднородного уравнения. Метод вариации произвольных постоянных Лагранжа. Комплексные решения дифференциальных уравнений. Построение фундаментальной системы решений
- •1. Структура общего решения неоднородного уравнения. Метод вариации произвольных постоянных Лагранжа
- •2.Метод вариации произвольных постоянных Лагранжа
- •3. Комплексные решения дифференциальных уравнений. Линейная независимость комплексных решений
- •Лекция 5. Линейные дифференциальные уравнения с постоянными коэффициентами. Метод Эйлера и метод подбора вычисления частных решений неоднородных уравнений
- •1. Метод Эйлера построения общего решения однородного дифференциального уравнения с постоянными коэффициентами в случае простых корней характеристического уравнения
- •2. Построение общего решения однородного дифференциального уравнения в случае кратных корней характеристического уравнения
- •3. Построение общего решения неоднородного уравнения с постоянными коэффициентами. Метод подбора частного решения неоднородного уравнения
- •Лекция 6. Комплексные числа и действия над ними. Функции комплексного переменного. Предел и непрерывность. Элементарные функции комплексного переменного и действия над ними
- •1. Извлечение корня й степени из комплексного числа. Множества в комплексной плоскости
- •2. Предел и непрерывность функции комплексной переменной
- •Лекция 7. Производная функции комплексного переменного. Аналитичность функции в точке и в области. Условия Коши-Римана. Элементарные аналитические функции
- •2. Геометрический смысл модуля и аргумента производной
- •Лекция 8 . Интеграл от функции комплексного переменного. Теорема Коши и для односвязной и многосвязной областей. Интегральная формула Коши. Существование всех производных для аналитической функции
- •2.2. Теорема Коши для односвязной области и многосвязной области. Интегральная формула Коши
- •3. Первообразная функции комплексных переменных
- •Лекция 9. Ряды в комплексной области. Степенные ряды. Теорема Абеля. Ряды Тейлора и Лорана
- •1. Степенные ряды. Ряды Тейлора и Лорана
- •Лекция 10. Изолированные особые точки. Ряды Лорана для функций, аналитических в кольце
- •1. Разложение функции в ряд Лорана
- •2. Нули аналитической функции и их связь с полюсами
- •3. Вычеты. Теорема Коши о вычетах
- •Лекция 11. Вычисление вычетов и применение теории вычетов для вычисления контурных и несобственных интегралов
- •1. Вычисление вычетов
- •2. Вычисление интегралов
- •Лекция 12. Преобразование Лапласа и его свойства. Применение к дифференциальным уравнениям
- •Лекция 13. Системы дифференциальных уравнений. Общие понятия
- •1. Понятия общего и частного решений. Задача Коши и ее разрешимость
- •2. Методы интегрирования систем дифференциальных уравнений
- •Лекция 14. Системы линейных дифференциальных уравнений
- •1. Глобальная теорема разрешимости начальной задачи для линейной системы дифференциальных уравнений
- •2. Линейная зависимость и линейная независимость системы произвольных вектор-функций и решений однородной системы уравнений
- •3. Фундаментальная матрица решений и структура общего решения однородной системы
- •4. Структура общего решения неоднородной системы дифференциальных уравнений
- •Лекция 15. Построение фундаментальной матрицы решений дифференциальной системы с постоянной матрицей. Метод Эйлера.
3. Комплексные решения дифференциальных уравнений. Линейная независимость комплексных решений
Напомним, что комплексными числаминазывают числа вида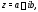 где
где и
и – действительные числа,
– действительные числа,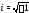 –– мнимая единица (
–– мнимая единица (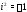 ).
При этом
).
При этом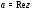 называется действительной частью,
а
называется действительной частью,
а – мнимой частьюкомплексного числа
– мнимой частьюкомплексного числа .
Число
.
Число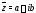 называется сопряженнымчислу
называется сопряженнымчислу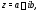 а неотрицательное число
а неотрицательное число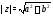 называется модулемчисла
называется модулемчисла .
Множество всех комплексных чисел
обозначают буквой
.
Множество всех комплексных чисел
обозначают буквой .
Каждому комплексному числу
.
Каждому комплексному числу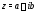 соответствует единственная точка
соответствует единственная точка на плоскости
на плоскости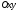 или радиус-вектор
или радиус-вектор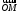 этой точки. При этом ось
этой точки. При этом ось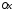 называется действительной осью, с
ось
называется действительной осью, с
ось – мнимой осью. Сама плоскость
– мнимой осью. Сама плоскость называется комплексной плоскостью;
ее тоже обозначают буквой
называется комплексной плоскостью;
ее тоже обозначают буквой .
Угол
.
Угол называется аргументомкомплексного
числа
называется аргументомкомплексного
числа .
Ясно, что аргумент определяется
неоднозначно. Главным значениемаргумента называется угол
.
Ясно, что аргумент определяется
неоднозначно. Главным значениемаргумента называется угол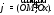 лежащий
в пределах
лежащий
в пределах (или в пределах
(или в пределах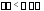 ).
Главное значение аргумента обозначается
так:
).
Главное значение аргумента обозначается
так: .
Из рис. 1 видно, что
.
Из рис. 1 видно, что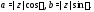 Значит, комплексное число можно записать
еще в виде
Значит, комплексное число можно записать
еще в виде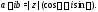 Эта форма называется тригонометрической
формойчисла
Эта форма называется тригонометрической
формойчисла ,
а его первоначальная форма
,
а его первоначальная форма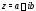 –алгебраической формой комплексного
числа
–алгебраической формой комплексного
числа .
Если воспользоваться формулой Эйлера
.
Если воспользоваться формулой Эйлера
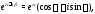 то
можно получить еще одну форму комплексного
числа
то
можно получить еще одну форму комплексного
числа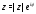 называемую показательной формойчисла
называемую показательной формойчисла .
.
Два комплексных числа называются равными, если равны одновременно порознь действительные и мнимые части этих чисел, т.е.
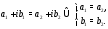
Действия над комплексными числами определяются равенствами:
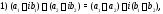
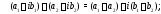
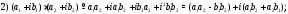
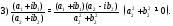
Умножение комплексных чисел (и их деление) лучше производить в тригонометрической форме:

Отсюда вытекает известная фoрмула
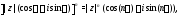
называемая формулой Муавра. С
помощью нее можно определить операцию
извлечения корня -й
степени из комплексных чисел.
-й
степени из комплексных чисел.
Определение 2.Отображение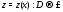 ,
ставящее в соответствие каждому
действительному числу
,
ставящее в соответствие каждому
действительному числу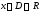 единственное комплексное число
единственное комплексное число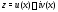
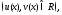 называется комплексной функцией
действительной переменной
называется комплексной функцией
действительной переменной с областью определения
с областью определения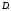
Над такими функциями можно производить обычные арифметические действия. Например,
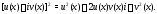
Комплексная экспонента вычисляется по формуле Эйлера
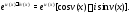
Отсюда легко получить формулы для синуса и косинуса комплексного аргумента:
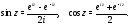
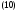
Производные комплексной функции действительного аргумента определим равенствами:

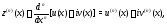
а интеграл – равенством
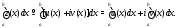
Например,
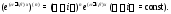
Пусть теперь дано дифференциальное уравнение

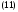
в котором участвуют только функции
действительного аргумента (в том числе
и комплексные функции действительной
переменной
 ).
Комплексное решение этого уравнения
определяется так же, как и действительное
решение: функция
).
Комплексное решение этого уравнения
определяется так же, как и действительное
решение: функция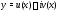 называется решением уравнения (11) на
отрезке
называется решением уравнения (11) на
отрезке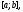 если она, будучи подставлена в уравнение
(11), обращает его в тождество на отрезке
если она, будучи подставлена в уравнение
(11), обращает его в тождество на отрезке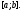 Задача Коши для уравнения (11) ставится
аналогично (только здесь начальная
точка может быть комплексной). Нас будет
интересовать линейное дифференциальное
уравнение
Задача Коши для уравнения (11) ставится
аналогично (только здесь начальная
точка может быть комплексной). Нас будет
интересовать линейное дифференциальное
уравнение

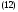
с действительными коэффициентами
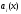 и с комплексной неоднородностью
и с комплексной неоднородностью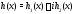 (
(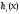 и
и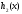 – действительные функции). Ясно, что
оператор
– действительные функции). Ясно, что
оператор остается линейным и в пространстве
остается линейным и в пространстве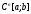 комплекснозначных функций. Докажем
следующее утверждение.
комплекснозначных функций. Докажем
следующее утверждение.
 Если
Если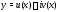 комплексное решение уравнения (12) с
действительными коэффициентами
комплексное решение уравнения (12) с
действительными коэффициентами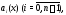 то его действительная
то его действительная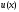 и мнимая
и мнимая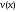 части являются решениями уравнений
части являются решениями уравнений
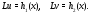
В самом деле, в силу линейности
оператора
 имеем
имеем
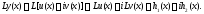
Приравнивая здесь отдельно действительную и мнимую части, получаем тождества
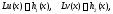
ч.т.д.
Полагая здесь
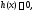 получаем следующий результат.
получаем следующий результат.
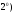 Действительная и мнимая части комплексного
решения
Действительная и мнимая части комплексного
решения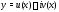 однородного дифференциального уравнения
однородного дифференциального уравнения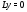 с действительными коэффициентами
с действительными коэффициентами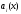 также являются решениями этого уравнения
(т.е.
также являются решениями этого уравнения
(т.е.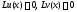 ).
).
Линейная зависимость и линейная
независимость на отрезке
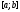 системы комплекснозначных функций
системы комплекснозначных функций определяется так же, как и для системы
действительных функций. Только здесь
коэффициенты
определяется так же, как и для системы
действительных функций. Только здесь
коэффициенты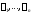 линейной комбинации могут быть
комплексными числами. Все теоремы 1–8
предыдущей лекции остаются в силе и для
комплексных решений.
линейной комбинации могут быть
комплексными числами. Все теоремы 1–8
предыдущей лекции остаются в силе и для
комплексных решений.
В дальнейшем потребуется факт линейной независимости некоторых систем комплекснозначных и действительных функций, описанных ниже.
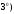 Система функций
Система функций
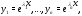
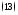
где все числа
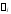 (комплексные или действительные) попарно
различны (т.е.
(комплексные или действительные) попарно
различны (т.е.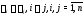 )
линейно независима на произвольном
отрезке
)
линейно независима на произвольном
отрезке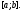
Доказательство.Запишем вронскиан
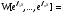
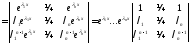
(здесь из каждого столбца вынесли общий
множитель – соответствующую экспоненту).
Стоящий здесь определитель (его называют
определителем Вандермонда) равен
произведению двучленов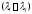 для всех
для всех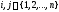 таких, что
таких, что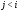 ,
т.е.
,
т.е.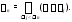 Этот факт можно показать по индукции,
но мы не будем этого делать. Проверим
его только для определителя Вандермонда
Этот факт можно показать по индукции,
но мы не будем этого делать. Проверим
его только для определителя Вандермонда
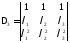
третьего порядка. Прибавляя ко второй
строке определителя
 его первую строку, умноженную на (
его первую строку, умноженную на ( ),
а к третьей строке – вторую, умноженную
на (
),
а к третьей строке – вторую, умноженную
на (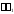 ),
будем иметь
),
будем иметь
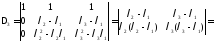
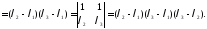
Итак, определитель Вронcкого
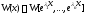 имеет вид
имеет вид

Поскольку у нас
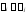 при
при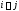 (
(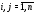 )
и экспонента в нуль не обращается, то
)
и экспонента в нуль не обращается, то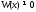 на любом отрезке
на любом отрезке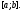 Свойство
Свойство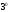 доказано.
доказано.
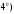 Пусть дана система действительных
функций
Пусть дана система действительных
функций



Если числа
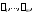
 попарно различны, то указанная система
функций линейно независима на любом
отрезке
попарно различны, то указанная система
функций линейно независима на любом
отрезке
Доказательство.Проведем его для системы функций
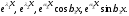
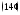
Составим их линейную комбинацию и приравняем ее нулю:
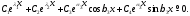
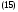
Используя формулы
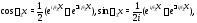
перепишем предыдущее тождество (15) в виде

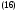
где обозначено:
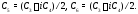 По условию числа
По условию числа попарно не равны друг другу, но тогда
попарно не равны друг другу и числа
попарно не равны друг другу, но тогда
попарно не равны друг другу и числа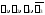 (учесть, что
(учесть, что и
и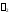 – действительные числа). По свойству
– действительные числа). По свойству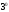 система функций
система функций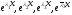 линейно независима на любом отрезке
линейно независима на любом отрезке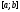 .
Значит, тождество (16) имеет место тогда
и только тогда, когда одновременно
.
Значит, тождество (16) имеет место тогда
и только тогда, когда одновременно
Из равенств
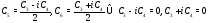
получаем, что тогда и числа
 Итак, в тождестве (15) все числа
Итак, в тождестве (15) все числа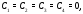 a значит система функций
a значит система функций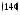 линейно независима на любом отрезке
линейно независима на любом отрезке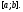 Свойство
Свойство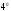 доказано.
доказано.
Аналогичными рассуждениями может быть доказано следующее утверждение.
 Если числа
Если числа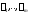 попарно не равны друг другу, то система
функций
попарно не равны друг другу, то система
функций
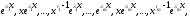
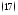
где
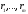 –
натуральные числа (
–
натуральные числа (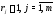 ),
линейно независимы на произвольном
отрезке
),
линейно независимы на произвольном
отрезке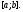 Линейно независимой будет также система,
образованная действительными и мнимыми
частями функций (17).
Линейно независимой будет также система,
образованная действительными и мнимыми
частями функций (17).

