
- •3 Семестр (часть 1). Дифференциальные уравнения
- •1. Общие понятия
- •3. Дифференциальные уравнения с разделяющимися переменными. Однородные уравнения
- •1. Линейные дифференциальные уравнения. Метод вариации произвольной постоянной
- •2. Задача Коши. Теорема существования и единственности решения задачи Коши. Общее решение и общий интеграл
- •3. Уравнения, допускающие понижение порядка
- •1. Свойства дифференциального оператора. Теорема Коши
- •2. Линейная зависимость и линейная независимость системы функций. Вронскиан. Исследование линейной независимости с помощью вронскиана
- •3. Структура общего решения однородного дифференциального уравнения
- •Лекция 4. Общее решение неоднородного уравнения. Метод вариации произвольных постоянных Лагранжа. Комплексные решения дифференциальных уравнений. Построение фундаментальной системы решений
- •1. Структура общего решения неоднородного уравнения. Метод вариации произвольных постоянных Лагранжа
- •2.Метод вариации произвольных постоянных Лагранжа
- •3. Комплексные решения дифференциальных уравнений. Линейная независимость комплексных решений
- •Лекция 5. Линейные дифференциальные уравнения с постоянными коэффициентами. Метод Эйлера и метод подбора вычисления частных решений неоднородных уравнений
- •1. Метод Эйлера построения общего решения однородного дифференциального уравнения с постоянными коэффициентами в случае простых корней характеристического уравнения
- •2. Построение общего решения однородного дифференциального уравнения в случае кратных корней характеристического уравнения
- •3. Построение общего решения неоднородного уравнения с постоянными коэффициентами. Метод подбора частного решения неоднородного уравнения
- •Лекция 6. Комплексные числа и действия над ними. Функции комплексного переменного. Предел и непрерывность. Элементарные функции комплексного переменного и действия над ними
- •1. Извлечение корня й степени из комплексного числа. Множества в комплексной плоскости
- •2. Предел и непрерывность функции комплексной переменной
- •Лекция 7. Производная функции комплексного переменного. Аналитичность функции в точке и в области. Условия Коши-Римана. Элементарные аналитические функции
- •2. Геометрический смысл модуля и аргумента производной
- •Лекция 8 . Интеграл от функции комплексного переменного. Теорема Коши и для односвязной и многосвязной областей. Интегральная формула Коши. Существование всех производных для аналитической функции
- •2.2. Теорема Коши для односвязной области и многосвязной области. Интегральная формула Коши
- •3. Первообразная функции комплексных переменных
- •Лекция 9. Ряды в комплексной области. Степенные ряды. Теорема Абеля. Ряды Тейлора и Лорана
- •1. Степенные ряды. Ряды Тейлора и Лорана
- •Лекция 10. Изолированные особые точки. Ряды Лорана для функций, аналитических в кольце
- •1. Разложение функции в ряд Лорана
- •2. Нули аналитической функции и их связь с полюсами
- •3. Вычеты. Теорема Коши о вычетах
- •Лекция 11. Вычисление вычетов и применение теории вычетов для вычисления контурных и несобственных интегралов
- •1. Вычисление вычетов
- •2. Вычисление интегралов
- •Лекция 12. Преобразование Лапласа и его свойства. Применение к дифференциальным уравнениям
- •Лекция 13. Системы дифференциальных уравнений. Общие понятия
- •1. Понятия общего и частного решений. Задача Коши и ее разрешимость
- •2. Методы интегрирования систем дифференциальных уравнений
- •Лекция 14. Системы линейных дифференциальных уравнений
- •1. Глобальная теорема разрешимости начальной задачи для линейной системы дифференциальных уравнений
- •2. Линейная зависимость и линейная независимость системы произвольных вектор-функций и решений однородной системы уравнений
- •3. Фундаментальная матрица решений и структура общего решения однородной системы
- •4. Структура общего решения неоднородной системы дифференциальных уравнений
- •Лекция 15. Построение фундаментальной матрицы решений дифференциальной системы с постоянной матрицей. Метод Эйлера.
3. Структура общего решения однородного дифференциального уравнения
Рассмотрим однородное линейное дифференциальное уравнение
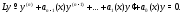
Докажем следующий важный результат.
Теорема 5.
Пусть функции
 являются решениями однородного уравнения
(5) с непрерывными на отрезке
являются решениями однородного уравнения
(5) с непрерывными на отрезке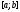 коэффициентами
коэффициентами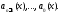 Тогда
Тогда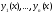 линейно независимы на отрезке
линейно независимы на отрезке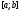 в том и только в том случае, когда
вронскиан
в том и только в том случае, когда
вронскиан этих функций не равен нулю ни в одной
точке отрезка
этих функций не равен нулю ни в одной
точке отрезка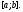
Доказательство.
Достаточность
вытекает из следствия 1. Докажем
необходимость. Пусть решения
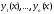 уравнения (5) линейно независимы на
отрезке
уравнения (5) линейно независимы на
отрезке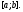 Покажем, что тогда вронскиан не обращается
в нуль ни в одной точке отрезка
Покажем, что тогда вронскиан не обращается
в нуль ни в одной точке отрезка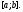 Предположим противное, т.е. что существует
точка
Предположим противное, т.е. что существует
точка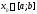 такая, что вронскиан
такая, что вронскиан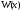 обращается в нуль в этой точке:
обращается в нуль в этой точке:
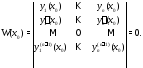
Тогда столбцы этого
определителя линейно зависимы, т.е.
существуют числа
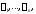 не равные нулю одновременно, такие, что
не равные нулю одновременно, такие, что
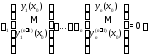
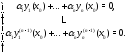
С помощью указанных
чисел построим функцию
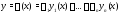 .
Поскольку
.
Поскольку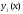 решения однородного уравнения (5), то из
линейности дифференциального оператора
решения однородного уравнения (5), то из
линейности дифференциального оператора следует, что
следует, что
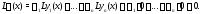
Это означает, что
функция
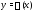 является решением уравнения (5). Из (6)
следует, что эта функция удовлетворяет
нулевым начальным условиям, т.е.
является решением уравнения (5). Из (6)
следует, что эта функция удовлетворяет
нулевым начальным условиям, т.е.
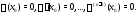
Но таким же начальным
условиям удовлетворяет и тривиальное
решение
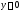 этого уравнения. В силу единственности
решения (см. теорему 1) функции
этого уравнения. В силу единственности
решения (см. теорему 1) функции и
и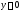 совпадают на отрезке
совпадают на отрезке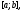 и значит
и значит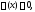 и значит
и значит
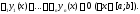
Поскольку здесь не
все числа
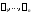 равны нулю, то последнее тождество
означает, что функции
равны нулю, то последнее тождество
означает, что функции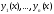 линейно зависимы на отрезке
линейно зависимы на отрезке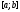 .
Мы получили противоречие, которое
показывает, что наше предположение
.
Мы получили противоречие, которое
показывает, что наше предположение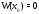 не верно. Следовательно, вронскиан не
обращается в нуль ни в одной точке
отрезка
не верно. Следовательно, вронскиан не
обращается в нуль ни в одной точке
отрезка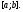 Теорема доказана.
Теорема доказана.
Из теоремы 4 и
доказательства теоремы 5 вытекают
следующие свойства вронскиана
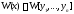 системы решений
системы решений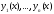 линейного однородного дифференциального
уравнения (5) с непрерывными на отрезке
линейного однородного дифференциального
уравнения (5) с непрерывными на отрезке коэффициентами
коэффициентами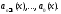
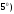 Если вронскиан
Если вронскиан
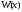 обращается в нуль в некоторой точке
обращается в нуль в некоторой точке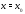 отрезка
отрезка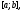 то он тождественно равен нулю на всем
отрезке
то он тождественно равен нулю на всем
отрезке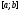 (т.e.
(т.e.
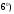 Если вронскиан
Если вронскиан
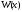 не равен нулю хотя бы в одной точке
не равен нулю хотя бы в одной точке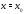 отрезка
отрезка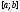 ,
то он не равен нулю и на всем отрезке
,
то он не равен нулю и на всем отрезке
Свойства
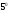 и
и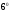 легко усматриваются также из формулы
легко усматриваются также из формулы
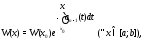
называемой формулой
Остроградского-Лиувилля. Здесь
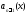 – коэффициент при производной
– коэффициент при производной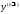 в уравнении (5),
в уравнении (5),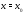 – произвольная фиксированная точка
отрезка
– произвольная фиксированная точка
отрезка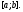
Обозначим теперь
через
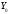 множество всех решений
множество всех решений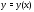 однородного уравнения (5). Какова структура
множества
однородного уравнения (5). Какова структура
множества ?
Во-первых, оно является линейным
пространством. Действительно, если
?
Во-первых, оно является линейным
пространством. Действительно, если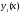 и
и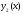 два произвольных элемента множества
два произвольных элемента множества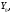 то выполняются тождества
то выполняются тождества а значит для произвольных чисел
а значит для произвольных чисел и
и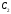 (в силу линейности оператора
(в силу линейности оператора )
имеет место тождество
)
имеет место тождество
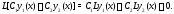
Это тождество
показывает, что любая линейная комбинация
элементов множества
 принадлежит
принадлежит (т.е. является решением уравнения (5)).
Следовательно,
(т.е. является решением уравнения (5)).
Следовательно,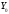 –- линейное пространство.
–- линейное пространство.
Из линейной
алгебры известно, что если линейное
пространство
 конечномерно, то в нем можно выделить
базис, т.е. такую упорядоченную систему
элементов
конечномерно, то в нем можно выделить
базис, т.е. такую упорядоченную систему
элементов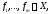 которая обладает свойствами:
которая обладает свойствами:
а) система
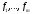 линейно независима;
линейно независима;
б) каков бы ни был
элемент
 ,
существуют числа
,
существуют числа такие, что
такие, что
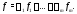
При этом числа
 называются координатами элемента
называются координатами элемента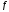 в базисе
в базисе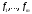 (показывается, что координаты элемента
в данном базисе единственны).
(показывается, что координаты элемента
в данном базисе единственны).
В пространстве
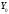 также можно выделить базис. В случае
дифференциальных уравнений (а также в
случае любой линейной системы уравнений)
базис пространства решений принято
называть фундаментальной системой
решений. Мы вернемся к этому термину
немного позднее и определим его более
точно.Существование базиса в
также можно выделить базис. В случае
дифференциальных уравнений (а также в
случае любой линейной системы уравнений)
базис пространства решений принято
называть фундаментальной системой
решений. Мы вернемся к этому термину
немного позднее и определим его более
точно.Существование базиса в устанавливается следующей теоремой.
устанавливается следующей теоремой.
Теорема 6 (о
структуре общего решения однородного
уравнения).
Если в уравнении
(5) все коэффициенты
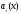 непрерывны на отрезке
непрерывны на отрезке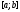 ,
то для него существуют
,
то для него существуют линейно независимых на отрезке
линейно независимых на отрезке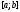 решений
решений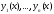 (
( – порядок уравнения (5)). При этом любое
другое решение уравнения (5) является
линейной комбинацией указанных линейно
независимых решений
– порядок уравнения (5)). При этом любое
другое решение уравнения (5) является
линейной комбинацией указанных линейно
независимых решений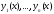 ,
т.е. общее решение уравнения (5) описывается
формулой
,
т.е. общее решение уравнения (5) описывается
формулой
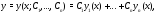

где
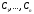 –- произвольные постоянные.
–- произвольные постоянные.
Доказательство.
Покажем сначала, что для уравнения (5)
существуют
 линейно независимых на отрезке
линейно независимых на отрезке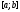 решений. Возьмем произвольную постоянную
матрицу
решений. Возьмем произвольную постоянную
матрицу с определителем
с определителем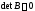 и со столбцами
и со столбцами Так что матрица
Так что матрица не вырождена и имеет порядок
не вырождена и имеет порядок .
Каждый столбец этой матрицы будем
использовать в качестве начальной точки
для задачи Коши для уравнения (21.5).
Получим
.
Каждый столбец этой матрицы будем
использовать в качестве начальной точки
для задачи Коши для уравнения (21.5).
Получим задач Коши:
задач Коши:
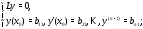

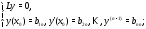
Каждая из этих задач
(в силу непрерывности коэффициентов
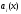 )
имеет единственное решение. Обозначим
через
)
имеет единственное решение. Обозначим
через решения этих задач соответственно.
Вронскиан в точке
решения этих задач соответственно.
Вронскиан в точке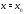 этих решений:
этих решений:
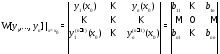
совпадает с
определителем
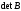 матрицы
матрицы ,
и поэтому не равен нулю. Отсюда следует,
что решения
,
и поэтому не равен нулю. Отсюда следует,
что решения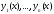 линейно независимы на отрезке
линейно независимы на отрезке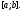 Существование таких решений доказано
(их можно даже построить бесчисленное
множество, выбирая произвольно матрицу
Существование таких решений доказано
(их можно даже построить бесчисленное
множество, выбирая произвольно матрицу с
с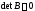 ).
Покажем теперь, что (8) – общее решение
уравнения (5).
).
Покажем теперь, что (8) – общее решение
уравнения (5).
При любых значениях
постоянных
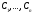 функция (8) является решением уравнения
(5), так как пространство
функция (8) является решением уравнения
(5), так как пространство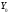 решений уравнения (5) является линейным
пространством. Пусть теперь
решений уравнения (5) является линейным
пространством. Пусть теперь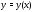 – решение произвольной задачи Коши
– решение произвольной задачи Коши
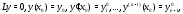
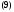
где
 Покажем, что существуют значения
постоянных
Покажем, что существуют значения
постоянных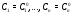 такие, что функция
такие, что функция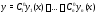 совпадает с решением
совпадает с решением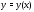 задачи Коши (9). Подчиняя (8) начальным
условиям (9), получаем равенства
задачи Коши (9). Подчиняя (8) начальным
условиям (9), получаем равенства
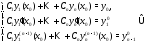


Так как решения
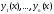 линейно независимы на отрезке
линейно независимы на отрезке то их вронскиан
то их вронскиан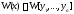 не равен нулю в произвольной точке
отрезка
не равен нулю в произвольной точке
отрезка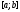 .
Определитель системы (10) совпадает с
вронскианом
.
Определитель системы (10) совпадает с
вронскианом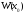 ,
и значит он не равен нулю. Но тогда
система уравнений (10) имеет единственное
решение
,
и значит он не равен нулю. Но тогда
система уравнений (10) имеет единственное
решение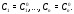 При этом функция
При этом функция являясь решением уравнения (5), удовлетворяет
и начальным условиям (9) (в силу выбора
чисел
являясь решением уравнения (5), удовлетворяет
и начальным условиям (9) (в силу выбора
чисел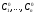 ).
Следовательно, функция (8) является общим
решением уравнения (5). Теорема доказана.
).
Следовательно, функция (8) является общим
решением уравнения (5). Теорема доказана.
Из этой теоремы
следует, что любая система из
 линейно независимых решений
линейно независимых решений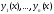 уравнения (5) порядка
уравнения (5) порядка образует базис (фундаментальную систему
решений (см. ниже)) в пространстве
образует базис (фундаментальную систему
решений (см. ниже)) в пространстве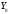 .
.
Определение 3.
Любая упорядоченная система из
 линейно независимых на отрезке
линейно независимых на отрезке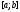 решений
решений уравнения (5) (
уравнения (5) ( -го
порядка) называется
фундаментальной системой решений
этого уравнения (или базисом его решений).
-го
порядка) называется
фундаментальной системой решений
этого уравнения (или базисом его решений).
Следовательно,
пространство
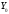 решений однородного уравнения (5) имеет
размерность
решений однородного уравнения (5) имеет
размерность .
На следующей лекции будет рассмотрено
неоднородное уравнение и изучена
структура его общего решения.
.
На следующей лекции будет рассмотрено
неоднородное уравнение и изучена
структура его общего решения.
