2.2. Теорема Коши для односвязной области и многосвязной области. Интегральная формула Коши

Напомним, что множество называетсяодносвязным,если любой замкнутый контур, лежащий вможно стянуть в точку, не выходя из. Множествоназываетсясвязным,если его границасостоит изпопарно не пересекающихся между собой замкнутых контуров.

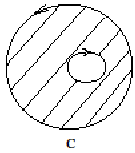
Например, на рисунке A изображена односвязная область, на рисунке B – 4-связная область (одна внешняя граница и три внутренних границ). При этом будем говорить, что направление на границе являетсяположительным (– положительно ориентирована), если при её обходе область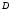остаётсяслева. Например, на рисунке C граница двухсвязной области положительно ориентирована. Ориентация, противоположная положительной, называетсяотрицательной.

Теорема Коши для односвязной области. Пусть область односвязная и функция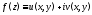аналитична вТогда каков бы ни был кусочно-гладкий замкнутый контурлежащий внутриинтеграл отпоравен нулю.

Доказательство. Вычислим интеграл

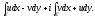
Воспользуемся формулой Грина:

где 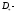область, охватываемая контуромБудем иметь

(здесь в квадратных скобках выписаны условия Коши-Римана, которые выполняются, так как функция аналитична в области). Теорема доказана.

Теорема Коши для многосвязной области. Пусть область 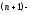связна,причемеё внешняя граница, аеё внутренние границы, обходимые все против часовой стрелки. Пусть функция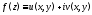аналитична вТогда имеет место равенство

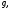Доказательство проведём для двухсвязной областиСделаем разрезсоединяющий внутреннюю и внешнюю границы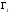иТогда областьбудет односвязной, а замкнутый контурлежит вЗначит, для этого контура справедлива предыдущая теорема:Применяя свойство аддитивности интеграла, будем иметь

Рис. 10Учитывая, чтоприходим к равенству

Остаётся учесть что здесь контуры иобходятся против часовой стрелки. Теорема доказана.

И, наконец, сформулируем без доказательство следующее важное утверждение.

Интегральная теорема Коши.Пусть функция аналитична в односвязной области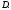Тогда какова бы ни была точка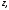лежащая внутри областии замкнутый кусочно-гладкий контур, охватывающий точкуи обходимый против часовой стрелки, справедливаинтегральная формула Коши

При этом функция имеет всюду впроизводные любого порядка, для которых справедлива формула

Замечание.Если функция аналитична в замкнутой ограниченной области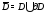с кусочно гладкой границейто в качестве контурав (6) можно взять границуТогда из (5) вытекает, чтоаналитическая в 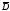функцияполностью определяется своими значениями на границеТаким свойством действительные функции не обладают.

Интегральная формула Коши имеет многочисленные применения, о которых будет сказано в дальнейшим. Рассмотрим несколько примеровⁱ.

Пример 1. Вычислить

Решение.Внутри окружностизнаменатель дроби обращается в нуль в точке. Для удобства применения формулы (5) перепишем интеграл в виде

Здесь ианалитична в круге. Тогда.

Пример 2. Вычислить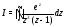: по

а) контуру ; б).

Решение. а) В кругефункцияаналитична. Следовательно, по теореме Коши для односвязной области получаем, что.

Рис. 11

б) Так как внутри контура интегрирования знаменатель подынтегральной функции обращается в нуль в точках и, то для того, чтобы стало возможным применить формулу (5), рассмотрим многосвязную область(рис. 11), ограниченную окружностьюи внутренними контурамии.

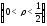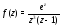Тогда в области функцияявляется аналитической, и по теореме Коши для многосвязной области можно записать:

Для вычисления интегралов справа применим формулу (5):

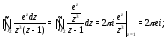
Таким образом, .