
- •3 Семестр (часть 1). Дифференциальные уравнения
- •1. Общие понятия
- •3. Дифференциальные уравнения с разделяющимися переменными. Однородные уравнения
- •1. Линейные дифференциальные уравнения. Метод вариации произвольной постоянной
- •2. Задача Коши. Теорема существования и единственности решения задачи Коши. Общее решение и общий интеграл
- •3. Уравнения, допускающие понижение порядка
- •1. Свойства дифференциального оператора. Теорема Коши
- •2. Линейная зависимость и линейная независимость системы функций. Вронскиан. Исследование линейной независимости с помощью вронскиана
- •3. Структура общего решения однородного дифференциального уравнения
- •Лекция 4. Общее решение неоднородного уравнения. Метод вариации произвольных постоянных Лагранжа. Комплексные решения дифференциальных уравнений. Построение фундаментальной системы решений
- •1. Структура общего решения неоднородного уравнения. Метод вариации произвольных постоянных Лагранжа
- •2.Метод вариации произвольных постоянных Лагранжа
- •3. Комплексные решения дифференциальных уравнений. Линейная независимость комплексных решений
- •Лекция 5. Линейные дифференциальные уравнения с постоянными коэффициентами. Метод Эйлера и метод подбора вычисления частных решений неоднородных уравнений
- •1. Метод Эйлера построения общего решения однородного дифференциального уравнения с постоянными коэффициентами в случае простых корней характеристического уравнения
- •2. Построение общего решения однородного дифференциального уравнения в случае кратных корней характеристического уравнения
- •3. Построение общего решения неоднородного уравнения с постоянными коэффициентами. Метод подбора частного решения неоднородного уравнения
- •Лекция 6. Комплексные числа и действия над ними. Функции комплексного переменного. Предел и непрерывность. Элементарные функции комплексного переменного и действия над ними
- •1. Извлечение корня й степени из комплексного числа. Множества в комплексной плоскости
- •2. Предел и непрерывность функции комплексной переменной
- •Лекция 7. Производная функции комплексного переменного. Аналитичность функции в точке и в области. Условия Коши-Римана. Элементарные аналитические функции
- •2. Геометрический смысл модуля и аргумента производной
- •Лекция 8 . Интеграл от функции комплексного переменного. Теорема Коши и для односвязной и многосвязной областей. Интегральная формула Коши. Существование всех производных для аналитической функции
- •2.2. Теорема Коши для односвязной области и многосвязной области. Интегральная формула Коши
- •3. Первообразная функции комплексных переменных
- •Лекция 9. Ряды в комплексной области. Степенные ряды. Теорема Абеля. Ряды Тейлора и Лорана
- •1. Степенные ряды. Ряды Тейлора и Лорана
- •Лекция 10. Изолированные особые точки. Ряды Лорана для функций, аналитических в кольце
- •1. Разложение функции в ряд Лорана
- •2. Нули аналитической функции и их связь с полюсами
- •3. Вычеты. Теорема Коши о вычетах
- •Лекция 11. Вычисление вычетов и применение теории вычетов для вычисления контурных и несобственных интегралов
- •1. Вычисление вычетов
- •2. Вычисление интегралов
- •Лекция 12. Преобразование Лапласа и его свойства. Применение к дифференциальным уравнениям
- •Лекция 13. Системы дифференциальных уравнений. Общие понятия
- •1. Понятия общего и частного решений. Задача Коши и ее разрешимость
- •2. Методы интегрирования систем дифференциальных уравнений
- •Лекция 14. Системы линейных дифференциальных уравнений
- •1. Глобальная теорема разрешимости начальной задачи для линейной системы дифференциальных уравнений
- •2. Линейная зависимость и линейная независимость системы произвольных вектор-функций и решений однородной системы уравнений
- •3. Фундаментальная матрица решений и структура общего решения однородной системы
- •4. Структура общего решения неоднородной системы дифференциальных уравнений
- •Лекция 15. Построение фундаментальной матрицы решений дифференциальной системы с постоянной матрицей. Метод Эйлера.
2. Геометрический смысл модуля и аргумента производной
Пусть функция
 дифференцируема в точке
дифференцируема в точке и
и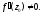 При отображении
При отображении вектор
вектор исходящий из точки
исходящий из точки переходит в
переходит в

Рис. 8
бесконечно малый вектор

 исходящий из точки
исходящий из точки а гладкая кривая
а гладкая кривая переходит в гладкую кривую
переходит в гладкую кривую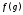 (см. рис. 8). Поскольку
(см. рис. 8). Поскольку то выполняются одновременно следующие
соотношения:
то выполняются одновременно следующие
соотношения:

Отсюда
следует, что с точностью до
 выполняются равенства
выполняются равенства
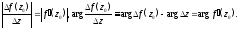
Эти равенства позволяют сделать следующие выводы (геометрический смысл модуля и аргумента производной ):
а) модуль
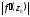 равен коэффициенту растяжения (сжатия)
бесконечно малого вектора
равен коэффициенту растяжения (сжатия)
бесконечно малого вектора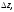 исходящего из точки
исходящего из точки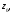 при отображении
при отображении
б) аргумент
 равен углу поворота
равен углу поворота бесконечно малого вектора
бесконечно малого вектора исходящего из точки
исходящего из точки при отображении
при отображении
Эти утверждения
верны для произвольного бесконечно
малого вектора
 исходящего из точки
исходящего из точки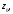 причем
утверждение б) будет верно для любых
гладких кривых
причем
утверждение б) будет верно для любых
гладких кривых исходящих из точки
исходящих из точки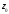 (в этом случае вектор
(в этом случае вектор касается кривой
касается кривой в точке
в точке ).
Если
).
Если и
и две гладкие кривые, исходящие из точки
две гладкие кривые, исходящие из точки то
из утверждения б) следует, что при
отображении
то
из утверждения б) следует, что при
отображении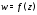 они развернутся на один и тот же угол,
т.е. угол между кривыми
они развернутся на один и тот же угол,
т.е. угол между кривыми и
и при отображении
при отображении сохраняется. Более того, сохраняется и
направление этого угла. Исходя из
сказанного, вводят следующее понятие.
сохраняется. Более того, сохраняется и
направление этого угла. Исходя из
сказанного, вводят следующее понятие.
Определение 4.
Отображение
 окрестности
окрестности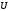 точки
точки на окрестность
на окрестность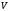 точки
точки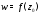 называетсяконформным,
если оно обладает постоянством растяжения
(сжатия) бесконечно малых элементов
называетсяконформным,
если оно обладает постоянством растяжения
(сжатия) бесконечно малых элементов
 и сохранением углов и их направлением
между любыми двумя гладкими кривыми
и сохранением углов и их направлением
между любыми двумя гладкими кривыми Отображение
Отображение называется
конформным в
области
называется
конформным в
области
 ,
если оно конформно в каждой точке области
,
если оно конформно в каждой точке области
 и если функция
и если функция является аналитической и однолистной
в области
является аналитической и однолистной
в области .
.
Теорема 2.
Пусть функция
 – однолистная и аналитическая в области
– однолистная и аналитическая в области и
и в каждой точке области
в каждой точке области .
Тогда отображение
.
Тогда отображение будет конформным в области
будет конформным в области .
.
Доказательство
этого утверждения вытекает из
геометрического смысла производной и
ее аргумента. Например, главная ветвь
логарифма

 является
конформным отображением области
является
конформным отображением области
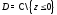 на область
на область Конформные отображения играют важную
роль в прикладных науках. Однако подробное
их изучение в нашем курсе не позволяет
дефицит времени. Читателю, заинтересованному
в более детальном ознакомлении с теорией
конформных отображений, рекомендуем
книгу Б.А. Фукса и Б.В. Шабата ``Функции
комплексного переменного и некоторые
их приложения'' (ГИФМЛ, Москва, 1959) .
Конформные отображения играют важную
роль в прикладных науках. Однако подробное
их изучение в нашем курсе не позволяет
дефицит времени. Читателю, заинтересованному
в более детальном ознакомлении с теорией
конформных отображений, рекомендуем
книгу Б.А. Фукса и Б.В. Шабата ``Функции
комплексного переменного и некоторые
их приложения'' (ГИФМЛ, Москва, 1959) .
======================================================
Лекция 8 . Интеграл от функции комплексного переменного. Теорема Коши и для односвязной и многосвязной областей. Интегральная формула Коши. Существование всех производных для аналитической функции
Везде ниже, если не оговорено противное,
функция
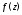 предполагается однозначной в своей
области определения. Пусть в плоскости
предполагается однозначной в своей
области определения. Пусть в плоскости задана некоторая ориентированная кривая
задана некоторая ориентированная кривая (
( начало,
начало, конец). Каждой точке
конец). Каждой точке плоскости
плоскости соответствует единственное комплексное
число
соответствует единственное комплексное
число (и обратно), поэтому будем отождествлять
точку
(и обратно), поэтому будем отождествлять
точку и соответствующее комплексное число
и соответствующее комплексное число и будем писать
и будем писать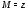 Пусть функция
Пусть функция определена на кривой
определена на кривой .
Разобъём кривую
.
Разобъём кривую на частичные дуги
на частичные дуги точками
точками в направлении ориентации кривой:
в направлении ориентации кривой:

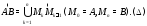
Возьмём произвольно точку
 и составим интегральную сумму
и составим интегральную сумму Обозначим
Обозначим диаметр разбиения
диаметр разбиения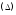 .
.
Определение 5. Если существует конечный предел интегральных сумм:

и он не зависит от вида разбиения
 и выбора точек
и выбора точек ,
то его называют интегралом от функции
,
то его называют интегралом от функции вдоль кривой (дуги)
вдоль кривой (дуги) и обозначают
и обозначают При этом функцию
При этом функцию называетсяинтегрируемой на кривой
называетсяинтегрируемой на кривой .
.
Сразу же отметим свойство ориентированности этого интеграла:

которое вытекает из того, что при
ориентации кривой от
 до
до вектор
вектор заменяется на вектор
заменяется на вектор Кроме того, интеграл от комплексной
функции, очевидно, обладает свойствами
линейности и аддитивности, которые мы
не выписываем. Следующее утверждение
позволяет свести комплексный интеграл
к двум действительным криволинейным
интегралам.
Кроме того, интеграл от комплексной
функции, очевидно, обладает свойствами
линейности и аддитивности, которые мы
не выписываем. Следующее утверждение
позволяет свести комплексный интеграл
к двум действительным криволинейным
интегралам.
Теорема 3.Пусть ограниченная дуга
 кусочно-гладка и лежит вобласти
кусочно-гладка и лежит вобласти
 определения функии
определения функии .
Пусть, кроме того,
.
Пусть, кроме того, непрерывна на дуге
непрерывна на дуге .Тогда имеет место равенство
.Тогда имеет место равенство

Доказательство.Преобразуем в
интегральной сумме (5) слагаемое :
:

Тогда интегральная сумма в равенсте (5) примет вид

Здесь действительная часть является
интегральной суммой для криволинейного
интеграла
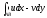 ,
а мнимая часть – интегральной суммой
для криволинейного интеграла
,
а мнимая часть – интегральной суммой
для криволинейного интеграла .
Так как функция
.
Так как функция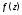 непрерывна на дуге
непрерывна на дуге то на этой дуге непрерывны ее действительная
часть
то на этой дуге непрерывны ее действительная
часть и мнимая часть
и мнимая часть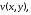 поэтому указанные криволинейные
действительные интегралы существуют.
Переходя к пределу в равенстве (7) при
поэтому указанные криволинейные
действительные интегралы существуют.
Переходя к пределу в равенстве (7) при получаем равенство (6). Теорема доказана.
получаем равенство (6). Теорема доказана.
Из этой теоремы вытекают свойства линейности, аддитивности и другие свойства комплексного интеграла. В частности, справедлива теорема об оценке интеграла.
Теорема 4. Если функция
 непрерывна на кусочно-гладкой ограниченной
кривой
непрерывна на кусочно-гладкой ограниченной
кривой то имеет место неравенство
то имеет место неравенство

где
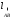 –
длина дуги.
–
длина дуги.
Из теоремы 3 вытекает также следующее утверждение.
Теорема 5. Пусть дуга
 задана параметрически уравнением
задана параметрически уравнением
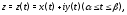
причем функция
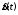 непрерывна на отрезке
непрерывна на отрезке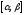 и дуга
и дуга ориентирована по возрастанию
параметра
ориентирована по возрастанию
параметра
 (т.е.
(т.е. – начало,
– начало, конец
дуги
конец
дуги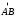 ).
Пусть, кроме того, функция
).
Пусть, кроме того, функция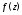 непрерывна на дуге
непрерывна на дуге .Тогда
имеет место равенство
.Тогда
имеет место равенство

В качестве примера вычислим имеющий
широкое применение в дальнейшей теории
интеграл
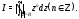 Покажем, что
Покажем, что

Имеем


Если
 то
то Если
Если то
то


Равенство
 доказано.
доказано.
