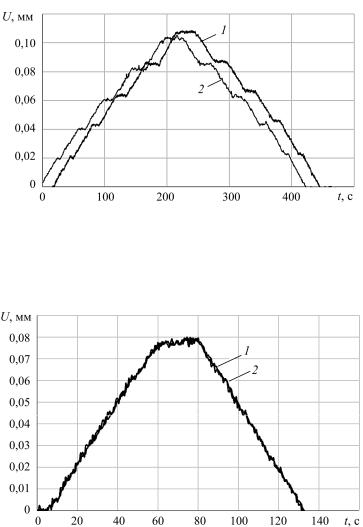
Рис. 2. Диаграмма зависимости перемещения от времени: 1 – исследуемая область Sраб = 0,0025 м2;
2 – исследуемая область Sраб = 0,0115 м2
Рис. 3. Диаграмма зависимости перемещения от времени: 1 – размер подмножества 51, шаг 5; 2 – размер подмножества 31, шаг 5
421
В ходе проделанной работы установлено влияние факторов корреляционной обработки (скорость съемки, время испытания, исследуемая область и размер подмножества) при реализации сложных режимов нагружения на экспериментальные данные, полученные при использовании метода КЦИ и Vic-3D.
Работа выполнена при поддержке гранта Президента РФ для государственной поддержки молодых российских ученых – кандидатов наук (МК-5172.2015.1), при финансовой поддержке Российского фонда фундаментальных исследований (проекты № 13-08-00304-а, 14-08-31387-мол).
Список литературы
1.Третьякова Т.В., Спаскова Е.М. Экспериментальное исследование напряженно-деформированных состояний квазихрупкого материала с использованием метода корреляции цифровых изображений // Вестник Пермского национального исследовательского политехнического университета. Механика. – 2013. –
№2. – С. 186–198.
2.Третьякова Т.В. Особенности использования программного обеспечения Vic-3D, реализующего метод корреляции цифровых изображений, в приложении к исследованию полей неупругих деформаций // Вычислительная механика сплошных сред. – 2014. – Т. 7, № 2. – С. 162–171.
3.Вильдеман В.Э, Третьякова Т.В, Лобанов Д.С. Методика экспериментального исследования закритического деформирования на образцах специальной усложненной конфигурации с применением метода корреляции цифровых изображений // Вестник Пермского государственного технического университе-
та. Механика. – 2011. – № 4. – С. 15–28.
ИНВАРИАНТНОЕ ПРЕДСТАВЛЕНИЕ ТЕНЗОРА УПРУГИХ МОДУЛЕЙ В ПОДХОДЕ АТОМАРНОЙ СТАТИКИ
С.С. Стволова, И.Ю. Зубко
(Пермский национальный исследовательский политехнический университет,
Пермь, Россия, zoubko@list.ru)
Получено инвариантное представление упругих модулей в виде сумм, построенных при использовании различных потенциалов межатомного взаимодействия. Вид потенциалов не конкретизируется, появляющиеся производные выражаются через силы межатомного взаимодействия, что позволяет исследовать возможности потенциалов для описания анизотропии и симметричности упругого отклика кристаллического материала. Также с помощью полученного инвариантного представления анализируется возможность применения потенциалов для исследования упругих свойств материалов с несимметричным тензором напряжений Коши.
Ключевые слова: дискретно-атомистическое моделирование, несимметричная упругость, прогнозирование упругих модулей кристаллов.
Работа посвящена исследованию структуры тензоров напряжений и упругих модулей с помощью потенциала межатомного взаимодействия. В общем виде потенциальная энергия системы атомов [1] представляется как
M |
M −1 M |
|
Φ = Φ1 (Ri ) + Φ2 (R j |
− Ri ) + |
i=1 |
i=1 j=i+1 |
|
M −2 M −1 M |
|
|
+ Φ3 (R j |
− Ri ,Rk − Ri ,Rk − R j ) + ... , |
i=1 j=i+1 k = j+1
где Ri – радиус-вектор, задающий положение i-го атома, M – полное число атомов образца, Φ1(Ri ) – часть потенциальной
энергии атомов, которая не зависит от их взаимодействия, а определяется полем некоторой внешней силы, Φ2 (R j − Ri ) – по-
тенциальная энергия парного взаимодействия или двухчастичный потенциал, Φ3 (R j − Ri ,Rk − Ri ,Rk − R j ) – трехчастичный
потенциал взаимодействия атомов. Двухчастичный потенциал межатомного взаимодействия характеризует изменение потенциальной энергии при изменении расстояния между парами атомов. Этот потенциал с помощью некоторой функциональной зависимости описывает, что при сближении два атома начинают отталкиваться, а при удалении притягиваться. Поскольку атомы нельзя сдвинуть бесконечно близко, то в ноле такая функция стремится к бесконечности. При увеличении расстояния между парой атомов эта функция выходит на горизонтальную асимптоту, а сила взаимодействия, модуль которой равен тангенсу угла наклона касательной к графику функции Φ2 (R j − Ri ) стремится
к нулю. Трехчастичный потенциал учитывает не только расстояние между двумя атомами, как в случае двухчастичного потенциала, но влияние конфигурации ближайших атомов. Например, трехчастичный потенциал может использоваться для описания ковалентной связи между соседними атомами в решетке графена или графита [2], находящимися в состоянии sp2-гибридизации. Силы взаимодействия каждого выбранного атома со всеми остальными атомами образца, вычисляемые с помощью двухчастичного потенциала, аддитивны. Для многочастичных потенциалов аддитивности сил взаимодействия нет. В рассматриваемом случае действие внешних сил не рассматривается, поэтому далее Φ1(Ri ) = 0 .
Для определения деформаций системы атомов необходимо задать две ее конфигурации: начальную и текущую. Для исследования механических свойств образца с кристаллической микроструктурой рассматриваются его конфигурации с однородным распределением атомов, каждая из которых характеризуется набором параметров межатомного расстояния (для простых решеток это один параметр, для сложных решеток параметров может быть несколько). Принимается, что отсчетная конфигурация является равновесной и может быть определена из условия минимума потенциальной энергии всего набора взаимодействующих атомов по параметрам решетки. Однородной

деформацией кристалла будем называть изменения длин и углов между прямыми линиями, соединяющими атомы, и линиями, описываемые тензором второго ранга, который соответствует однородному аффинору F (или тензору деформационного градиента, хотя для дискретной системы он не равен градиенту ка- кого-либо непрерывного поля), используемому в механике сплошных сред. В текущей конфигурации положение i-го атома задается вектором ri = F Ri (правило Коши–Борна).
Для расчета упругих модулей кристаллических систем в рамках статического подхода [2–4] принимается, что плотность упругой энергии и плотность потенциальной системы взаимодействующих атомов кристалла в текущей конфигурации совпадают. Тогда производные от плотности потенциальной энергии дискретной системы атомов по мерам деформации дадут выражения для вычисления компонент тензоров напряжений (с помощью первых производных) и компонент тензора линейно-упругих
свойств (вторые производные). Пусть Φˆ (F) – потенциальная
энергия однородно-деформированного кристаллического образца в текущей конфигурации. Энергия в отсчетной конфигурации, которая соответствует системе атомов с заданной кристаллической структурой и минимальным значением потенциальной энер-
ο
гии по параметрам решетки, равна Φ = Φˆ (I) . Относя изменение полной потенциальной энергии при деформировании кристалли-
ческого тела к его объему в отсчетной |
ο |
ˆ |
Ω |
или в текущей Ω кон- |
фигурации, будем получать соответствующую плотность энергии деформаций. Она используется для вычисления тензора напряжений Пиолы–Кирхгофа:
ο |
−1 |
ˆ |
ο |
T |
ο |
−1 |
ˆ |
T |
. |
(1) |
P1 = Ω |
|
∂(Φ(F) − Φ) ∂F |
|
= Ω |
|
∂Φ(F) ∂F |
|
Тензор напряжений Коши σ получается с использованием связи
σ = J −1F P1 ,
|
|
ˆ |
ο |
|
где |
|
Ω . Тогда тензор напряжений Коши |
J = det F = Ω / |
ˆ |
−1 |
ˆ |
T |
. |
σ = Ω |
|
F ∂Φ(F) ∂F |
|
|
Рассмотрим два вида представления потенциальной энер- |
гии в случае учета только двухчастичного взаимодействия, используя для простоты вместо набора векторных аргументов, соединяющих различные пары атомов, обозначение R в отсчетной конфигурации или r в текущей:
ˆ |
ˆ |
|
|
ˆ |
R) , где ( ) – упрощенное |
1) Φ(F) = Φ( |
r) = Φ(F |
обозначение суммы потенциалов (1) в текущей конфигурации, |
ˆ |
ˆ |
|
|
r |
|
ˆ |
|
F |
R |
|
ˆ |
R F |
T |
F R). |
|
|
|
|
2) Φ(F) = Φ( |
|
|
|
) = Φ( |
|
|
) = Φ( |
|
В первом случае существует возможность учета направления связи между различными парами атомов, во втором случае учитывается только расстояние между ними. Производная по тензору деформационного градиента F в этих двух случаях приводит к выражениям:
1. |
ˆ |
по аргументу r дает вектор силы |
Производная Φ′( r) |
f ( r), который определяется конкретным потенциалом межатомного взаимодействия:
|
|
|
|
|
|
|
|
|
|
|
|
ˆ |
|
T |
|
ˆ |
r) ∂(F R) ∂F |
T |
= R f ( r) |
|
∂Φ(F) ∂F |
|
= Φ′( |
|
|
|
|
ˆ |
−1 |
F |
R f ( |
ˆ |
−1 |
r f ( r) . |
(2) |
|
σ = Ω |
|
r) = Ω |
|
Для двухчастичных потенциалов векторы f ( r) и r коллинеарны, что вызывает симметрию тензора напряжений Коши. Для многочастичного взаимодействия (как в методе погруженного атома) направление силы f ( r) может не совпадать с направлением вектора r, соединяющего атомы, что приведет
кнесимметричности тензора напряжений Коши.
2.Производная Φˆ ′( r ) по скалярному аргументу является скалярной величиной, что приводит к выражению:

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ˆ |
T |
ˆ |
|
|
|
r |
|
) |
∂ |
|
R F |
T |
F |
R ∂F |
T |
= |
|
|
|
∂Φ(F) ∂F |
|
= Φ′( |
|
|
|
|
|
|
|
|
|
ˆ |
|
r |
|
) |
|
r |
|
−1 |
R r. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= Φ′( |
|
|
|
|
|
|
|
|
Следовательно, для тензора напряжений Коши получим
ˆ |
−1 ˆ |
|
r |
|
) r r |
|
r |
|
, |
(3) |
|
|
|
|
σ = Ω |
Φ′( |
|
|
|
|
т.е. тензор напряжений Коши будет симметричным для любого потенциала межатомного взаимодействия.
В случае учета только парного межатомного взаимодействия, когда потенциальная энергия представляется в виде
ˆ |
M −1 |
M |
ϕ(rj |
− ri ) , где |
ϕ(ri − rj ) – некоторый двух- |
Φ(F) = i=1 |
j=i+1 |
частичный потенциал, получим:
а) Φˆ ′ = iM=1−1 Mj=i+1 ϕ′(rj − ri ) ,
σ= Ωˆ −1 iM=1−1 Mj=i+1(rj − ri )ϕ′(rj − ri ) = Ωˆ −1 iM=1−1 Mj=i+1(rj − ri )f(ij) ,
причем в общем случае из этого представления следует, что
σT ≠ σ;
б) Φˆ ′ = iM=1−1 Mj=i+1 ϕ′( rj − ri ), σ= Ωˆ −1 iM=1−1 Mj=i+1(rj − ri )f(ij) ,
но в этом случае сила f(ij) = ϕ′( rj − ri )(rj − ri )
 rj − ri парного
rj − ri парного
межатомного взаимодействия действует по линии, соединяющей атомы, и получаемый тензор напряжений Коши состоит из суммы симметричных диад вида α(ij) (rj − ri )(rj − ri ) , т.е. являет-
ся симметричным σT = σ.
При учете многочастичного взаимодействия в методе погруженного атома потенциальная энергия системы определяется выражением, в котором учтено, что отталкивание всех атомов описывается согласно закону парного взаимодействия, а притяжение описывается нелинейной функцией γ (), задающей влияние окружения произвольного атома (функция погружения). Окружение определяетсямножествомномеров соседних атомов Si:

ˆ |
M −1 |
M |
ϕ |
+ |
|
|
|
|
M |
γ ( j Si |
− |
(rj |
− ri )). (4) |
|
|
|
Φ(F) = i=1 |
j=i+1 |
|
( |
|
rj − ri |
|
) + i=1 |
ϕ |
|
|
|
|
|
|
Функции ϕ± (rj − ri ) могут зависеть как только лишь от
расстояний между атомами, так и от расстояний и направлений действия межатомных сил в окрестности выбранного атома. Производная от первого слагаемого даст выражение, аналогичное полученной ранее сумме. Для второго слагаемого при использо-
вании обозначений r(ij) |
≡ rj − ri и (ϕ− (r(ij) ))′ ≡ f(−ij) получим: |
∂ γ ( j Si ϕ− (r(ij) )) |
∂FT = γ′( j Si ϕ− (r(ij) )) j Si R(ij)f(−ij) . |
Тогда тензор напряжений Коши можно представить в виде:
|
iM1−1 |
Mj i 1(ϕ+ )′ |
|
r(ij) |
|
−1 r(ij)r(ij) + iM1 |
(γ′( j S |
ϕ− (r(ij) )) j S |
r(ij)f(−ij) ) |
|
|
|
|
|
|
|
σ= |
= |
= + |
|
|
|
= |
i |
i |
. |
(5) |
|
|
|
|
|
ˆ |
|
|
|
|
|
|
|
|
|
Ω |
|
|
|
|
|
Поскольку вектор f(−ij) не обязательно направлен вдоль вектора r(ij) , то в результате получаемый тензор может быть не-
симметричным.
Для вычисления упругих модулей при малых деформациях необходимо найти производную от тензора напряжений Коши (5):
∂σ ∂FT = ∂Ωˆ −1
∂FT = ∂Ωˆ −1 ∂FT ( iM=1−1 Mj=i+1(ϕ+ )′ r(ij) −1 r(ij)r(ij ) +
∂FT ( iM=1−1 Mj=i+1(ϕ+ )′ r(ij) −1 r(ij)r(ij ) +
M |
|
− |
ˆ −1 |
M −1 |
M |
(ϕ |
+ |
)′ |
|
r(ij) |
|
−1 |
|
|
|
+ i=1 |
(γ′ j Si |
r(ij)f(ij) |
))+ Ω ∂ ( |
i=1 |
j=i+1 |
|
|
|
r(ij)r(ij) + |
|
|
+ iM=1(γ′ j Si |
r(ij)f(−ij ) )) ∂FT . |
|
|
|
|
|
|
Рассмотрим производные этого выражения по отдельности:

ˆ −1 |
∂F |
T |
ο −1 |
∂J |
−1 |
∂F |
T |
ˆ |
−1 |
−T |
, |
∂ Ω |
|
= Ω |
|
|
= −Ω |
F |
|
∂ r(ij)r(ij ) |
∂FT = (en r(ij ) + r(ij )en )R(ij)en , |
где en – ортонормированный базис внешней системы координат. Второе и третье слагаемые содержат следующие производные
∂(ϕ+ )′ |
|
r(ij) |
|
−1 |
r(ij)r(ij) |
= |
(ϕ+ )′′ |
|
r(ij) |
|
|
− (ϕ+ )′ |
r r |
R |
r |
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂FT |
|
|
|
|
r(ij) |
|
3 |
(ij) (ij) |
|
(ij) (ij) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+(ϕ+ )′ ((en r(ij) + r(ij)en )R(ij)en ), r(ij)
|
∂ (γ′ j Si r(ij)f(−ij) ) |
= γ′′ r f |
− |
|
R |
|
f |
|
− |
+ γ′ (e |
|
g |
|
|
|
+ r |
G |
|
e |
|
)R |
|
en |
, |
|
∂FT |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(ij) (ij) |
|
|
|
|
(ij) |
(ij) |
|
|
|
|
|
n |
|
(ij) |
|
(ij) |
|
(ij) |
|
n |
|
(ij) |
|
|
где производные γ′ |
и γ′′ функции γ имеют аргумент j Si |
ϕ− (r(ij) ) , |
тензор |
второго |
|
ранга |
|
|
|
|
|
|
G |
(ij) |
≡ ∂f − |
|
∂r |
|
= ∂2ϕ− (r |
|
) ∂r |
2 |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(ij) |
|
|
|
|
(ij) |
|
|
|
(ij) |
|
(ij) |
|
∂f(−ij) ∂FT |
= G(ij) enR(ij)en . В итоге получим тензор четвертого ран- |
га следующего строения: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂σ ∂F |
T |
|
|
ˆ −1 |
|
−T |
× |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= −Ω |
|
F |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
×( iM=1−1 Mj=i+1(ϕ+ )′ |
|
r(ij) |
|
−1 |
|
r(ij)r(ij) + iM=1(γ′ j S r(ij)f(−ij) ))+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ˆ −1 |
M −1 |
|
|
M |
|
|
|
+ |
)′′ |
|
r(ij) |
|
− |
(ϕ |
+ |
)′) |
|
r(ij) |
|
−3 |
r(ij)r(ij)R(ij)r(ij) + |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+Ω |
i=1 |
j=i+1{((ϕ |
|
|
|
|
|
|
|
|
|
|
+(ϕ+ )′ r(ij) −1 ((en r(ij) + r(ij)en )R(ij)en )}+
+Ωˆ −1 iM=1 j Si {γ′′ (r(ij)f(−ij) R(ij)f(−ij) )+
+γ′ (en f(−ij) + r(ij)G(ij) en )R(ij)en }.
R(ij)
f(−ij)
При условии малости деформаций F → I получим строение тензора линейно-упругих модулей для кристаллического материала в виде выражения:
ο |
|
|
M −1 |
M |
|
|
|
|
|
|
−1 R(ij)R(ij) + |
M (γ′ |
R(ij)f(−ij) ))+ |
C = −Ω−1 I( |
(ϕ+ )′ |
R(ij) |
|
|
|
i=1 |
j=i+1 |
|
|
|
|
|
|
|
|
|
i=1 |
j S |
ο |
|
iM=1−1 Mj=i+1{((ϕ+ )′′ |
|
|
− (ϕ+ )′) |
|
|
−3 R(ij)R(ij)R(ij)R(ij) + |
+ Ω−1 |
R(ij) |
R(ij) |
|
|
|
|
|
+(ϕ+ )′ |
|
R(ij) |
|
−1 (en R(ij) + R(ij)en )R(ij)en}+ |
(6) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ο |
M |
|
{γ′′ R(ij)f(−ij)R(ij)f(−ij) + γ′ (en f(−ij) |
+ R(ij)G(ij) en )R(ij)en}. |
+ Ω−1 |
|
|
i=1 |
|
j Si |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В общем случае данное выражение не обладает симметрией внутри пар первых и вторых диад, которая возможна только в случае коллинеарности векторов с векторами . В слу-
чае их коллинеарности и тождественной функции погружения γ для метода погруженного атома γ′ = 1, γ′′ = 0 тензор четвертого
ранга (6) становится изотропным.
Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований (грант № 14-01-00069,
грант № 15-01-08678).
Список литературы
1.Clayton J. Nonlinear Mechanics of Crystals. – London: Springer, 2011. – 715 p.
2.Зубко И.Ю. Вычисление упругих модулей монослоя графена в несимметричной постановке с помощью энергетиче-
ского подхода // Физическая мезомеханика. – 2015. – Т. 18,
№2. – С. 37–50.
3.Симонов М.В., Зубко И.Ю. Определение равновесных параметров решетки различных ГПУ-монокристаллов с помощью потенциала межатомного взаимодействия Ми // Вестник







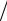

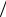 ∂
∂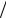 ∂
∂